「数直線」をわかりやすく解説（期末テスト対策ポイント）
yuminekoこのページでは、中学数学「正の数・負の数」を学習するときに登場する「数直線」というものが何かを解説するよ！
この「数直線」、実は前回の学習の時にもう使っているよ。
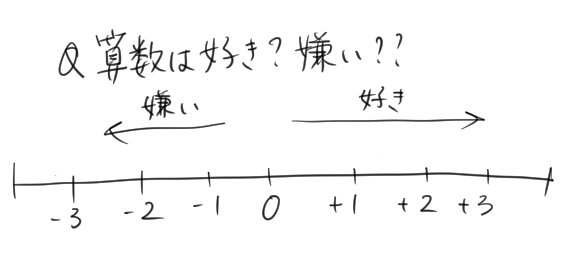
くまごろうこの「目盛りの線」って、「算数がどのくらい好き（嫌い）なのかを表しているんだよね。
もし、この目盛り線がなくて、ただ
「私は算数が＋1くらい好き」と文章であらわしたらどうかな？
＋1好きって言われても、何が基準になっているのかピンとこないし、どのくらい好きなのか分かりにくいよ・・
そうだね。
でも、目盛り線であらわしてもらえれば、＋1はどのくらい算数が好きな状態なのかイメージがつきやすいよね。
- ある数が「どのくらい多い」とか、「どのくらい強いのか」など、どんな状態を表すのかイメージがつきやすくなって便利だから！
- ある数字が、他の数字や「キホン」とどのくらい離れているのか分かりやすいから！
「数直線とは」
教科書にはなんて書いてあるの？
この点から左右に等しい間隔で目盛りをつけ、0よりも右側には正の数である「＋1」「＋2」「＋3」を順に対応させ、0よりも左側には負の数である「−1」、「−2」、「−3」を順に対応させたものを数直線と呼ぶ。 数直線上で、数0に対応している点のことを「原点」と呼ぶ。
また、数直線の右の方向を「正の方向」、左の方向を「負の方向」と呼ぶ。
たろう「基準の点」？「対応」って・・・？
なんだか全体的にピンとこないよ。
基準の点って？？
ザックリいうと
基準の点とは
「普通」や「スタート地点」というイメージ
数直線の「普通」や「スタート地点」が「基準の点」になる！
くまごろうさっきの数直線をもう一度見てみよう。
この数直線があらわしているのは「どのくらい算数が好き（嫌い）かどうか」だよね。
この時、真ん中ってどういう意味？
「好き」でも「嫌い」でもないということだよね。
・・・そうか、「普通」ということをあらわしているんだね！
ではこれはどうかな？
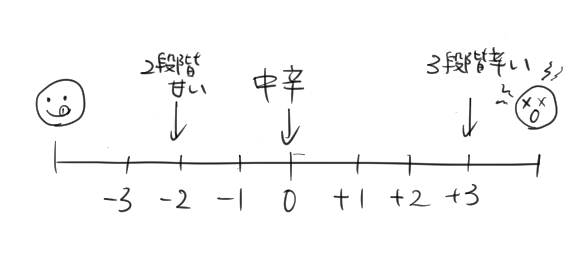
くまごろうこの数直線は、カレーがどのくらい辛いか（甘いか）をあらわしていて、基準の点は「辛くも、甘くもない普通の辛さ」だよね。
これの場合はどうだろう。
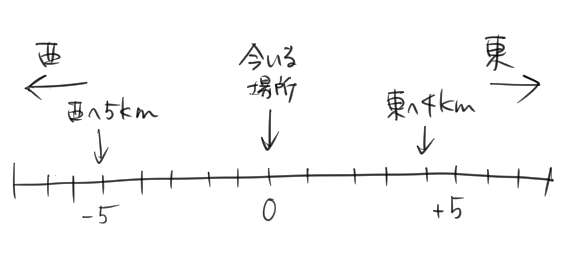
くまごろうこれは「スタート地点」である「今いる場所」が基準の点になっているんだね。
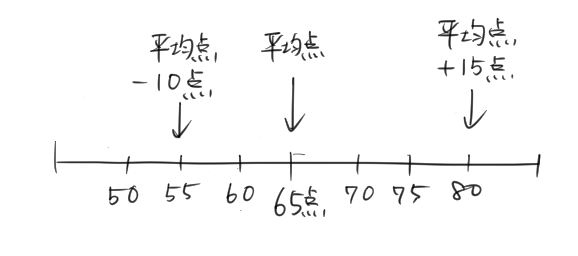
そうか。「平均点」はつまり「普通」ということだもんね。
だから平均点が基準の点になっているんだね。
数0を「対応させる」ってどういう意味なの？
ザックリいうと
対応させるとは、
「基準の点＝数0」とすること！
基準の点が決まったら、
そこを「数0」にする！
さっきの「平均点」の例で考えてみるよ。
くまごろう この数直線の「基準の点」である平均点は、65点なんだよね。
数直線では、この基準の点は実際の点数ではなくて、「数0」にしてしまう んだよ。
ちょっとまって。
そもそも、その「数0」ってどいういう意味？？
くまごろう「数0」というのは、単純に「数字の0」と考えてOKだよ。
「0」だけだと、アルファベットの「o（オー）」と区別するのが難しかったりするから、「数字の0だよ」とハッキリ伝えるために「数0」と言っているんだ。
基準の点を「数0」とすると、こうなるよ。
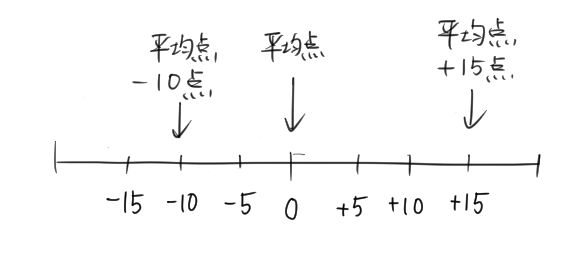
なるほど。
基準の点を「数0」にすると、それぞれの点が「基準（この場合、平均点）」に比べて、どのくらい良い点なのか、悪い点なのかがハッキリする ね。
原点とは
教科書くん数直線上で、数0に対応している点のことを「原点」と呼ぶ
また新しい言葉が出てきた！
くまごろうこれはカンタンな事を言っているよ。
さっきは「基準の点」を「数0」に対応させたよね。
だから「数0に対応している点」というのは、結局「基準の点」のことだよ。
つまり、「基準の点」＝「数0」＝「原点」というだけ。
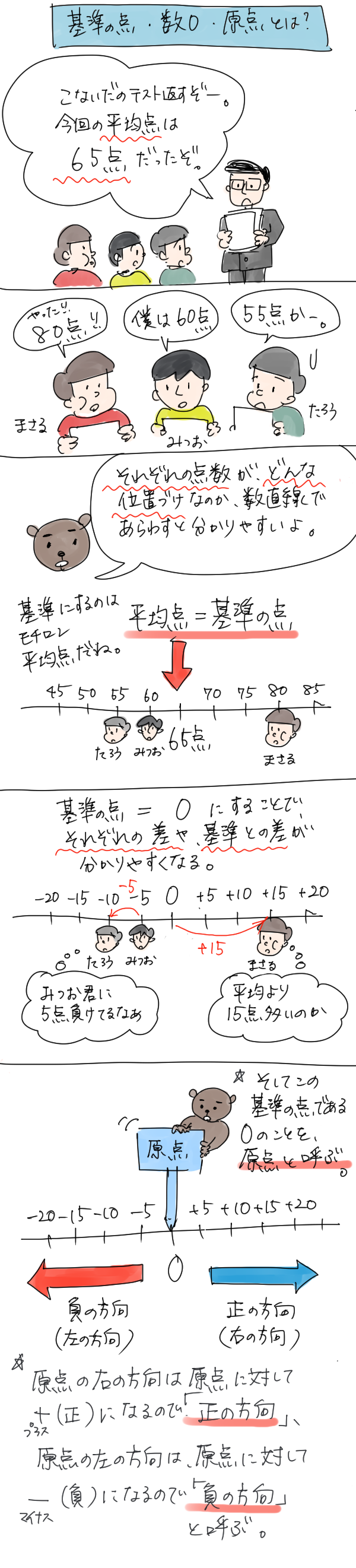
「正の方向」・「負の方向」について
この正の方向・負の方向だけれど、原点から考えたときだけではなく、「あるポイントから見て」どちらの方向か？という考え方もするよ。
例えば、同じ「負の数」同士の-5と-7で考えてみよう。
-5も-7も、原点から見たら「負の方向」にあるけれど、
-5は、-7から見たら「右の方向」にあるので、「-5は-7よりも正の方向にある」と言うんだ。
同じように、正の数同士の+4と+6で考えても、
+4は、+6から見たら「左の方向」にあるので、「負の方向」になるんだ。
こういう問題が出る！
yumineko実際の問題は、こういう風に出てくるよ
数直線の中の空欄（またはアルファベットなど）に入る数を答えるタイプ
次の数直線のA〜Dに当てはまる数を答えなさい
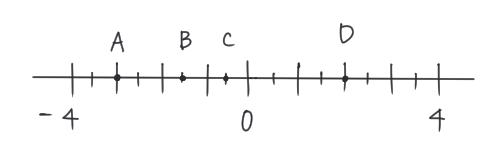
【考え方】
まずは ひとつの目盛りが、
「いくつをあらわしているのか」読み取ろう！
え？
目盛りって、必ず「1」ずつ増えたり減ったりするんじゃないの？
くまごろう この「ひとつの目盛りがいくつをあらわすか」は、数直線によって色々違う時があるんだ。
だから必ずチェックしないといけない。
1目盛りがいくつをあらわすのかをチェックする方法
①「分かっている」数字を探す。
くまごろうこの時みるポイントは、「数字が分かっているところ」。
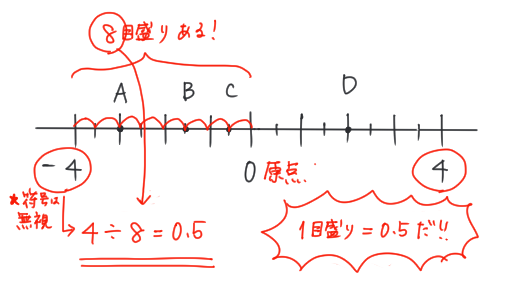
この問題の場合は、「−4」と「4」が分かっているよね。
②「見つけた数字」と、「原点」の間にいくつ目盛りがあるか数える
原点の0から「−4」まで※は、
8目盛りあるね。
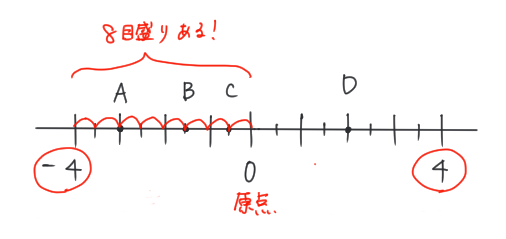
※もちろん、原点から「4」までを数えてもいいよ。
この場合も、目盛りは8つだよ。
③見つけた数字÷目盛りの数を計算する！
くまごろうこの時、見つけた数字の「符号」は無視してね。
例えば、見つけた数字が「−4」でも、符号は無視して「4÷8」で計算しよう。
こうして計算した結果が、「ひとつの目盛りが表す数」だよ。
この問題の場合は、「4÷8＝0.5」だから、ひと目盛りは「0.5」をあらわしているんだ。
くまごろうこれで答えをもとめるための準備はOK！
つぎは実際に、求める点が「いくつになるか」を計算するよ。
原点から求める点までの目盛り×目盛りがあらわす数を求める
①原点から求める点まで、何目盛りあるか数えよう！
くまごろうたとえば、Aの点を求めてみるよ。
原点からAまでは、6目盛りあるね。
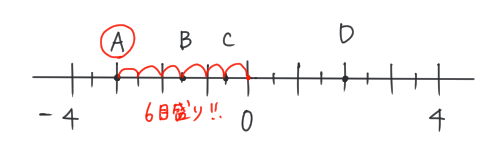
②ひと目盛りがあらわす数と、目盛りの数を「かける」
さっき求めた「ひと目盛りがあらわす数」は「0.5」だったね。
ということは、Aの点は「6×0.5＝3」だから、「3」だね！
くまごろう 答えの数字が出ても、まだ安心したらダメだよ。
「負の数」なのか、「正の数」なのか確認しよう！
求める点が原点よりも「負の方向」にあるなら「−」を、「正の方向」にあるなら「＋」をつける
くまごろう 求める点「A」は、原点よりも「負の方向」にあるね。
なので、求めた答えの「3」に「−」をつけて、「−3」が答えになるよ。
これでOK！
数直線の上に、対応する点を書き込むタイプ
次の数に対応する点を、数直線の上にしるしましょう。
-3.5
【考え方】
くまごろうこのタイプの問題でも、まずは「ひとつの目盛りがいくつをあらわすのか」を最初に考えるよ。
求めかたはさっきとおんなじ。
ひとつの目盛りは「0.5」をあらわすね。
「問題の数字」÷「ひとつの目盛りがあらわす数」をもとめる
問題の数字は「-3.5」だよね。
この「-3.5」を「0.5」で割るんだ。
「-3.5÷0.5＝-7」
計算の結果の「-7」から、「負の方向」に「7目盛り」進んだところが「対応する点」になるよ。
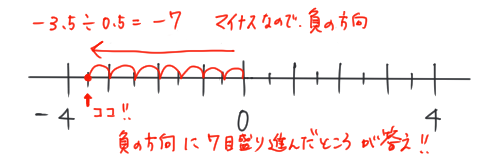
くまごろう計算の結果が「＋」だったら、「正の方向へ」、「−」だったら、「負の方向へ」進めばいいんだ。
中学数学ではココを押さえればOK！
数直線まとめ
- 「基準の点」とは、数直線の「普通」や「スタート地点」をあらわす点のこと。
- 「基準の点」＝数0で、この点を「原点」と呼ぶ。
- 原点の右の方向は「正の方向」と呼ぶ。
- 原点の左の方向は「負の方向」と呼ぶ。
- 【数直線の問題の解き方】
①分かっている数字を探し、原点からその数字まで何目盛りあるか数える。
②見つけた数字÷目盛りの数で、「ひと目盛りがいくつをあらわすのか」をもとめる。
※見つけた数字の符号は無視してOK数直線上の点に対応する数を求める場合
1：原点からの目盛りの数×②の答えをもとめる
2：点が負の方向にあるなら「−」、正の方向にあるなら「＋」をつけるある数が、数直線上のどの点に対応するか求める場合
1：その数÷②の答えをもとめる
2：1の答えが「−」なら負の方向に、「＋」なら正の方向に、答えの数だけ目盛りを勧める。
yumineko次は「数の大小」について解説するよ！
ここまで勉強したら、「正負の数」「数直線」「数の大小」についてのテスト対策問題のページに挑戦してみよう！
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
-
-
-
≪…「数直線」…≫は、人の形態空間（ニッチ）での時間軸的に眺望したい・・・
数直数には、1・2・3・4次元までの数の言葉ヒフミヨ（数体（次元））が、溶け込んでいる・・・数の言葉ヒフミヨ（1234）は、順序的構造・位相的構造・代数的構造 が自然数に内在（本性）しているようだ・・・
この風景は、3冊の絵本で・・・
絵本「哲学してみる」
絵本「わのくにのひふみよ」
絵本「もろはのつるぎ」 （有田川町ウエブライブラリー）
-
≪…「数直線」…≫は、人の形態空間（ニッチ）での時間軸的に眺望したい・・・
数直数には、1・2・3・4次元までの数の言葉ヒフミヨ（数体（次元））が、溶け込んでいる・・・数の言葉ヒフミヨ（1234）は、順序的構造・位相的構造・代数的構造 が自然数に内在（本性）しているようだ・・・
この風景は、3冊の絵本で・・・
絵本「哲学してみる」
絵本「わのくにのひふみよ」
絵本「もろはのつるぎ」 （有田川町ウエブライブラリー）
-
もろはのつるぎ（有田川町ウエブライブラリー）は、数の言葉ヒフミヨ（（1234）自然数）の『ＨＨＮＩ眺望』の眺めを、ＳＮＳの≪【インドの魔術師】ラマヌジャンの見つけたクールな式≫（検索）の［何かの機会に使う式］に『自然数製造機』（『自然比矩形』）を醸成していそうだ。
-
≪…真ん中ってどういう意味？「好き」でも「嫌い」でもないということだよね。
・・・そうか、「普通」ということをあらわしているんだね！…≫で、数学の基となる自然数（数の言葉ヒフミヨ（1234））を昭和歌謡の本歌取りで掴む・・・「愛のさざなみ」の本歌取り
[ i のさざなみ ］
この世にヒフミヨが本当にいるなら
〇に抱かれて△は点になる
ああ〇に△がただ一つ
ひとしくひとしくくちずけしてね
くり返すくり返すさざ波のように〇が△をきらいになったら
静かに静かに点になってほしい
ああ〇に△がただ一つ
別れを思うと曲線ができる
くり返すくり返すさざ波のようにどのように点が離れていても
点のふるさとは〇 一つなの
ああ〇に△がただ一つ
いつでもいつでもヒフミヨしてね
くり返すくり返すさざ波のように
さざ波のように［ヒフミヨ体上の離散関数の束は、［1］（連接）である。］
（複素多様体上の正則函数の層は、連接である。）数学の基となる自然数（数の言葉ヒフミヨ（1234））を大和言葉の【ひ・ふ・み・よ・い・む・な・や・こ・と】の平面・２次元からの送りモノとして眺めると、［岡潔の連接定理］の風景が、多くの歌手がカバーしている「愛のさざなみ」に隠されていてそっと岡潔数学体験館で、謳いタイ・・・
≪…数直線…≫の眺望を絵本で・・・
絵本「わのくにのひふみよ」