自然数と素数とは?素因数分解のやり方のコツとは「整数の性質」
「自然数と素数」とは?
「素因数分解」とは?
中学数学がはじまって、いきなり難しそうな言葉に、つい数学にニガテ意識をもってしまう子も多いんじゃないかな。
でも、数学はひとつひとつの単元をつみかさねていくことが大切な教科なんだ。
基本をきちんと理解していると、この先の単元もすんなり理解することができるようになるよ。
この記事では、自然数・素数・素因数分解についてわかりやすく解説して、定期テストを解くためのポイントを紹介するよ。
1とその数自身の積でしかあらわせない数を素数という。
ただし、1は素数ではない。
自然数を素数の積だけであらわすことを素因数分解という。
それでは、教科書の説明をわかりやすく解説していくよ!
自然数とは
1以上の整数を自然数という。
ここのポイントは、
・自然数は整数でなきゃいけない。つまり、小数や分数はダメなんだよね。
・1以上でないといけない。つまり、マイナスや「0」もダメなんだよね。
自然数を例でいうと
1、2、3、4、5、6、7、8、9、10・・・・。
要するにプラスの整数のことだね。
中学校の数学ではプラスのことを「正」というから、自然数とは「正の整数」と言い換えることもできるよ。
自然数の意味はそのまま、「自然な数」とイメージするといいよ。
物の個数を数えたり、順番を数えたりといった日常生活で、みんなが当たり前のように使う数だと思ってもらえたらオッケー。
そうすると、どうしてマイナスや「0」が含まれないかがわかるはず。
たとえば、リンゴをかぞえなきゃいけないときを想像してみて。
「リンゴがあるから」数えるんだよね。リンゴがないのに、わざわざ「リンゴが0コある」とは数えないよね。
ましてや、「リンゴがマイナス2コ」なんてことは、自然にはありえないことだよね。
とくに「自然数には0は入らない」というのは、テストでもひっかけ問題としてよく出てくるので、ここでしっかりおさえておこう!
自然数について、どうして「0」が含まれないのかを解説しているページもあるよ。
自然数と整数の違いは何?
自然数と整数はすごく似ていて、間違えやすいよね。
でも、自然数と整数の違いはすごくシンプル。
自然数は「正の整数」だけだったよね。
整数は、正の整数だけではなく、「0」や、0より小さい整数「マイナス」も入るよね。(マイナスの整数は「負の整数」と言い換えられるよ)
わかりやすくまとめると次のようなイメージ。
自然数 → 正の整数だけ
整数 → 負の整数 + 0 + 正の整数
素数とは
1とその数自身の積でしかあらわせない数を素数という。
ただし、1は素数ではない。
ここのポイントは、
・1は素数ではないこと!
「1とその数自身の積でしかあらわせない数」という言葉がむずかしいよね。
素数をわかりやすく簡単に言うと「1と、”自分自身の数”でしか割り切れない数」。
たとえば、「3」と「5」って、それぞれ「3」と「5」でしか割り切れないよね。
でも、「4」とか「6」はどう?
「4」は「2」でも割り切ることができるし、「6」も「3」で割り切ることができるよね。
「1」は、すべての数を割り切ることができるから、あたりまえのように登場しているよ。つまりスタメンみたいなものかな。
「1と、”自分自身の数”でしか割り切れない数」という条件で、素数かどうかを判定していくと、1~100までの素数は次の通り。
2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97
素数の覚え方
「えー!そんなに覚えられないよ・・・」という子がいっぱいいると思う。
ただ中学校の数学では「2、3、5、7、11」が素数であることを知っていれば解ける問題ばかりなので次のように覚えるのがおすすめだよ。
中学数学でよく出る素数の覚え方
兄さん(2、3)と午後(5、5)にセブンイレブン(7、11)に行く。
これだったら覚えられるね。
1は素数ではない!
さて、素数の大切なポイントのひとつは、「1は素数ではない」こと。
素数には、「約数が2つしかない数」という定義(ルール)があるんだよ。
約数というのは、「その数を割り切ることができる数」のこと。
さっきの「1と、その数自身でしか割り切ることができない」という言葉は、言い換えると「その数を割り切ることができるのは1とその数自身の2つ」。
つまり「約数は2つしかない」となるよね。
そうすると、「1」はどうかというと・・・
そう、「1」は約数が1つしかないよね。だって、「1」だけだから。
だから、「1」は素数の仲間入りはできないんだ。
でもなんでそんないじわるをするのかというと、「1」を素数にしてしまうと、「他の数がすべて素数ではなくなってしまう」からなんだ。
どうしてそんなことになってしまうかを説明するとすごく大変なのでここでは省略するけど、「1」って、どんな数でも割り切ることができるよね。
つまり、「スーパーチートアイテム」みたいなイメージ。
「1」を素数にしてしまうと、めちゃくちゃになってしまうので、「1」はナシね、となっているというわけだね。
素因数分解のやり方をマスターしよう!
素因数分解のやり方をマスターするために、まずは素因数分解とは何かを知ろう。
自然数を素数の積だけであらわすことを素因数分解という。
ある自然数のことを、「〇かける△」だよ、と素数のかけ算だけであらわすことを素因数分解というんだ。
例えば30という自然数で考えてみよう。
30は6×5と表すことができるよね。
ただ、これでは素因数分解したとはいえないんだよ。なぜなら6が素数ではないから。
だから6を分解して2×3にしたら、すべてが素数になるよね。
まとめると次のようになるね。
①30=6×5
→6が素数ではないから、素因数分解できていない。
②30=2×3×5
→2、3、5すべてが素数だから、素因数分解できている。
もう1問考えてみよう。
42という数を考えてみよう。①②どちらが素因数分解できているかわかるかな?
①42=2×3×7
②42=6×7
→もちろん答えは①だよ。2、3、7すべて素数だからね。一方②は6が素数ではないよね。
このように素因数分解っていうのは、自然数を素数の積(かけ算)で表すことをいうよ。
これは「料理」に例えてみると面白いよ。
たとえば、「ハンバーグ」があったとするよ。
ハンバーグを「できている材料で分解」してみよう。
牛ひき肉と、豚肉と、卵と、パン粉、玉ねぎと牛乳、ナツメグに塩コショウ・・
「パン粉」がまだ分解できるね。
牛ひき肉と、豚肉と、卵と、卵と、小麦粉と、さとう、イースト、バター・・・
こんなふうに、「もう分解できないよ」というところまで分解するイメージ。
「この自然数は、どんな数(素数)でできている数なのかな?」と分解してみるのが、素因数分解なんだね。
「因」っていう漢字は、「原因」とかでも使われるように、「もとになったこと」という意味だよね。
「素因数分解」は、「もとになっている素数で分解する」という意味の言葉なんだね。
素因数分解のひっ算
では最後に441を素因数分解してみよう。
「えー!!そんなおおきい数がどんな素数のかけ算になっているかなんて、さっぱりわからないよ!」ってなるよね。
そうだね、今のやり方で考えていては大変。
そこで、「素因数分解のひっ算」のやり方を覚える必要があるんだ。
ひっ算と言っても、これまでに使ってきた「足し算や引き算」の時とはちょっと違って、次のようなやり方をするよ。
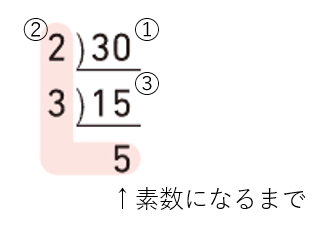
- 素因数分解したい数を書く。
- 右の数を割り切ることができる素数を書く。
- 商を書く。
※②と③を商が素数になるまで繰り返す。 - ④商が素数になったら、図で赤く示したところの積が答えになる。
さっき、「数が大くて無理!」と思った「441」を素因数分解してみると次のようになるよ。
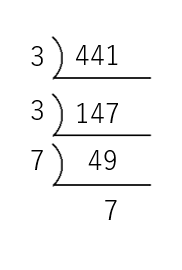
この結果から441=32×72
このひっ算を知っていれば簡単に素因数分解ができるよね。
素因数分解の裏ワザ・コツは?
素因数分解の裏ワザやコツを紹介するよ。素因数分解を早く解くには、割り切れる数を見つけるスピードが大事だよ。
1桁目が偶数だったら2で割り切れることは当たり前だよね。では、例えば、1113って何で割り切れるかわかるかな?
実は3で割り切れるんだよ。
そんないくつで割り切れるかを見つける裏ワザやコツを紹介するよ。マスターすることで素因数分解が速くなること間違いなし。
素数3で割り切れるか見分ける裏ワザ
素数3で割り切れるかどうかは、すべての桁の和が3の倍数になっているかどうかでわかるよ。
例えば、1113だったら、すべての桁の和は1+1+1+3=6で3の倍数になっている。だから3で割り切れるとわかるんだよ。
素数11で割り切れるか見分ける裏ワザ
3で割り切れるかを見つけるより複雑であまり使うことはないかもしれないけど、素数11で割り切れるか見分ける裏ワザもあるよ。
①同じ数字が偶数個ずつ並んでいる
(88、2288、224433など)
②奇数個の数字の繰り返しになっている
(345345、5614256142など)
③偶数桁の数字が、上から読んでも下から読んでも同じ数字になっている
(4554、65744756など)
素因数分解の問題に挑戦してみよう
素因数分解の問題に挑戦してみよう。
素因数分解の例題
24を素因数分解してみよう。
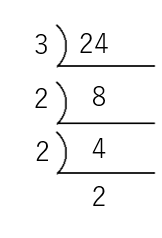
答え 24=23×3
素因数分解の問題(難しい)
243を素因数分解してみよう。
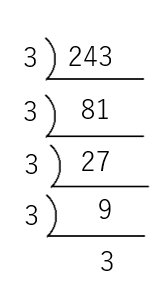
答え 243=35
素因数分解の問題(応用)
次の問題は素因数分解を利用した応用問題。まず素因数分解するところから始めてみよう。
問題:ある数を2乗すると1764になる。ある数を求めなさい。
【解説】
①1764を素因数分解すると次のようになるよね。
1764=22×32×72
②素因数分解の答えのかけ算の順番を変えてみるよ。
1764=22×32×72
=2×2×3×3×7×7
=2×3×7×2×3×7
=(2×3×7)×(2×3×7)
= 42 × 42
③42×42が1764になることがわかるかな?
なので答えは42になるんだ。
整数の性質まとめ
「自然数と素数」「素因数分解」についてわかったかな?
整数の中には自然数や素数という数字があって、素数を使うと素因数分解ができるんだよ。
中学数学がはじまって、いきなり難しそうな言葉に、つい数学にニガテ意識をもってしまう子も多いと思うので、整数の性質のまとめを下に乗せたよ。
整数の性質まとめ
- 整数はー3、ー2、ー1、0、1、2、3などで、0もマイナスも含まれる。
- 自然数は1、2、3などの正の整数で0やマイナスは含まない。
- 素数は1より大きい自然数で、1と自分自身でしか割り切れない数のこと。例:2、3、5、7、11・・・。
- 素因数分解とは素数の積で表すこと。例:30=2×3×5。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。





テスト練習問題とまとめ的なものを投稿していただきありがとうございます。
図やイラスト的なものを添えて解説してもらったおかげですごく分かりました。
全教科の復習の仕方詳しく載せたりしてもらえないでしょうか……。
学力テストで意外な点数をとってしまい絶望しました。
お願いです!!!!!!