ねじれの位置とは?簡単な見つけ方を紹介「直線や平面の位置関係」
中学1年生の数学で学習する「直線や平面の位置関係」について、「交線」とはどういうものか、「ねじれの位置」とはどういう位置関係のことなのかをわかりやすく説明しています。
「ねじれの位置」かどうかを簡単に判断する見つけ方を紹介するよ。
交線とは
「交線とは何か」の前に、「交点」について考えてみよう。交点っていうのは、線と線が交わったときにできる点のことをいうよ。
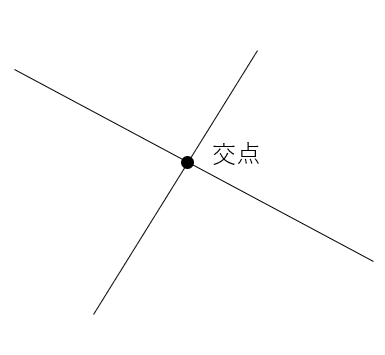
同じように考えると、「交線」というのは、面と面が交わったときにできる線のことだよ。
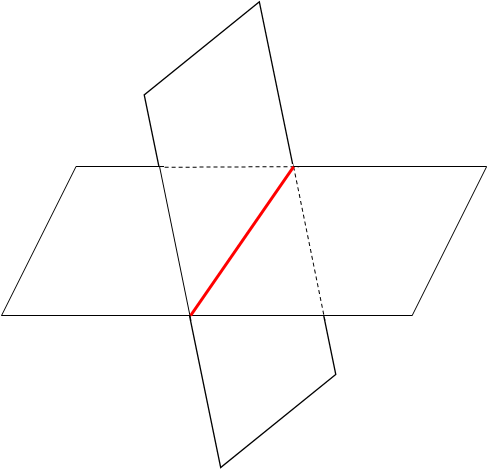
面と面が交わると、交わっているところは点ではなく、線になるよね。だから交線っていうんだね。
ねじれの位置とは
「ねじれの位置」なんて言われても、あんまりピンとこないかもしれないね。
だって、普段の生活で、「ねじれ」のことを意識することなんてあまりないよね。
でも1年生の図形の学習の中でも、「ねじれ」というのはすごく大事な言葉なんだ。
定期試験や入試問題にもよく出てくるところだからしっかり理解しよう。
2本の直線の関係を考えてみよう
ねじれの説明の前に、2本の直線の関係について確認しよう。
2本の直線があるとき、その2本の直線の関係は必ず、次のどれかにあてはまるんだよ。
①交わる ②平行 ③ねじれ
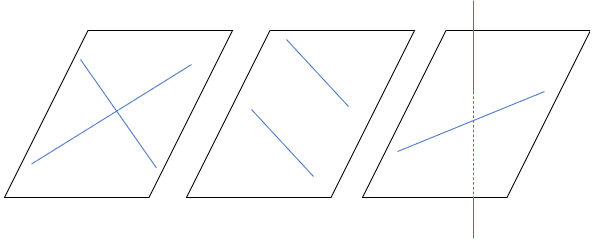
「①交わる」や「②平行」はイメージできるよね。
「③ねじれ」っていうのは、交わらないし、平行でもない関係のことをいうよ。
平面な図で説明すると、「交わる」と「ねじれ」の見た目の違いがあまりよくわからないかもしれないので、立体図で考えてみよう。
「直方体」のねじれの位置の問題
下の図形は直方体である。辺ABとねじれの辺を選びなさい。
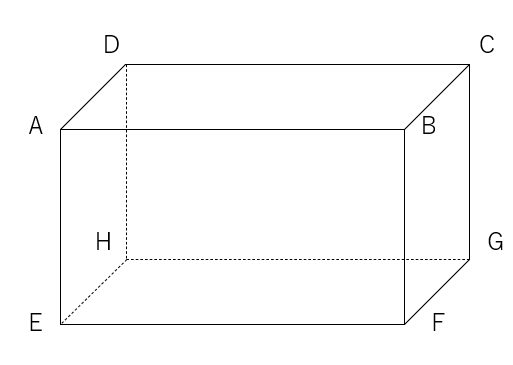
ねじれっていうのは、交わってもいないし、平行でないもののことだよね。
なので、「交わっている」ものと「平行」なものを候補から消していく「消去法」で考えよう。
そのためにまずは「交わっている辺」と「平行な辺」をそれぞれ見つけるよ。
①:交わっている辺を見つける
辺AB(赤線)と交わっている辺は青色の線で表したよ。
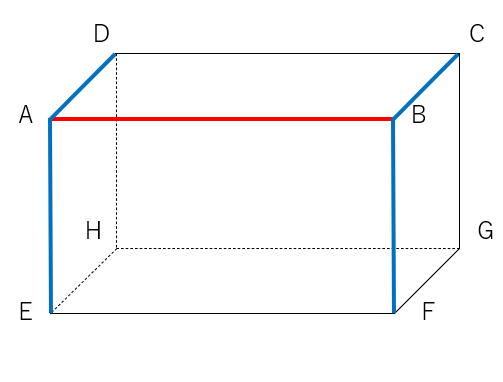
②:平行な辺を見つける
辺AB(赤線)と平行な辺は緑色の線で表したよ。
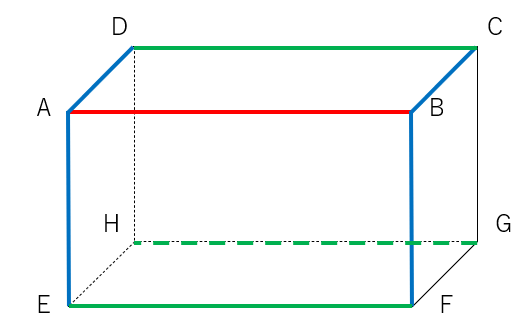
③:①②ではないものが「辺ABとねじれ」
交わってもいないし、平行でもないものが「ねじれ」なので、図でいうと、色のついていないところが「ねじれ」ということになるね。

だから、答えは、
辺DH、辺CG、辺EH、辺FG
だよ。
「三角柱」のねじれの位置の問題
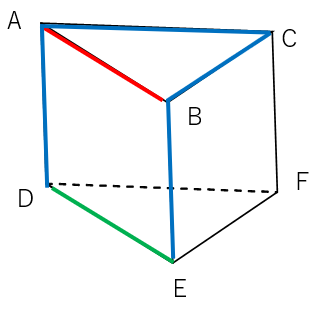
下の図形は三角柱である。辺ABとねじれの辺を選びなさい。
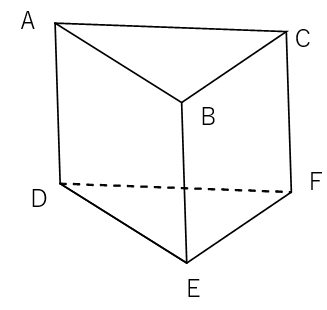
おなじく消去法で考えよう。
そのために「交わっている辺」と「平行な辺」をまず見つけるよ。
①:交わっている辺を見つける
辺AB(赤線)と交わっている辺は青色の線で表したよ。
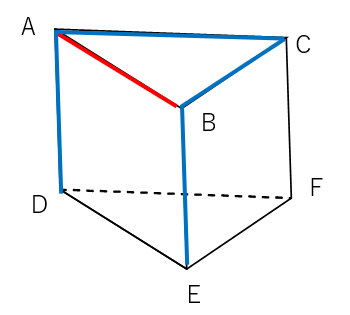
②:平行な辺を見つける
辺AB(赤線)と平行な辺は緑色の線で表したよ。
③:①②ではないものが「辺ABとねじれ」
交わってもいないし、平行でもないものが「ねじれ」なので、図でいうと、色のついていないところが「ねじれ」ということになるね。

だから、答えは、
辺CF、辺DF、辺EF
だよ。
ねじれの問題で間違えやすい「正五角柱のねじれの位置」
今までの問題をやってみて、「平行でもないし、交わってもいないものを探すだけなんて、簡単だよ」と思うかもしれないけれど、実は、間違えやすい問題があるんだよ。
下の正五角柱で、辺ABとねじれの位置にある辺を答えなさい。
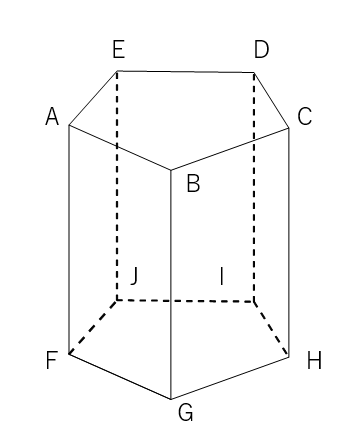
①:交わっている辺を見つける【要注意】
辺AB(赤線)と交わっている辺を青色の線で表したよ。
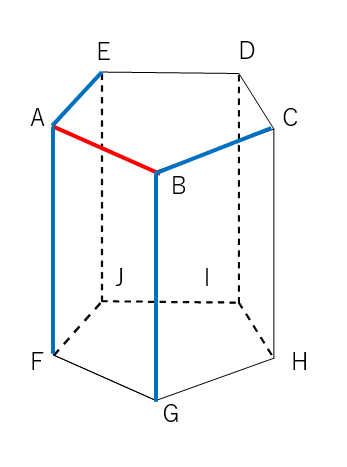
だけど、変ABと交わっている辺はこれだけじゃないんだよ。
「交わる」というのは、「2つの辺をずーっと伸ばした時に、交わる」のであれば、それも「交わる」というんだよ。
たとえば、辺DEをずーっと伸ばしてみて。
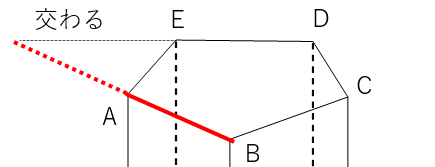
辺DEをずーっと伸ばしたら、辺ABをずーっと伸ばしたものと交わるね。
辺CDも、ずーっと伸ばしたらやっぱり辺ABをずーっと伸ばしたものと交わるよ。
なので、「辺DE」と「辺CD」も辺ABと交わるってことになるよ。
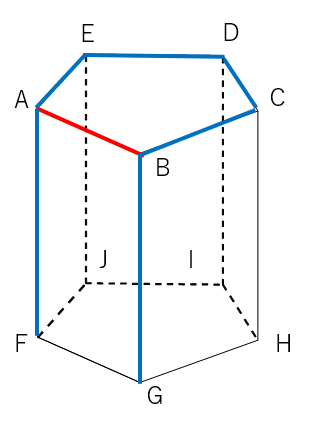
②:平行な辺を見つける
辺AB(赤線)と平行な辺は緑色の線で表したよ。
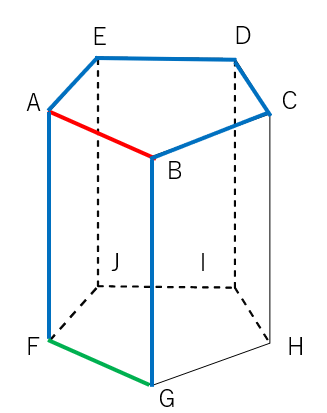
③:①②ではないものが「ABとねじれ」
交わってもいないし、平行でもないものが「ねじれ」なので、図でいうと、色のついていないところが「ねじれ」ということになるね。

だから、答えは、
辺FJ、辺GH、辺HI、辺IJ、辺CH、辺DI、辺EJ
だよ。
「交わる」辺を見つけるのが難しかったと思う。ずーっと延ばして交わるかを確認しなくちゃいけないってことだよ。
ちょっと頭を使うよね。でも、ねじれの性質を1つ知っておけば簡単にねじれを見つけられるので紹介するよ。
ねじれの性質
- 交わらないし、平行でもない
- 同じ平面上にない
「同じ平面上にない」とはどういうことかっていうと、下の図を見てみよう。
下の図は辺ABが含まれる平面を緑色で表しているよ。
2つの平面が当てはまるね。
「ねじれは、同じ平面上にない」ということは、つまり「緑色の平面上にある辺は絶対に、ねじれにはならない」ということだよ。
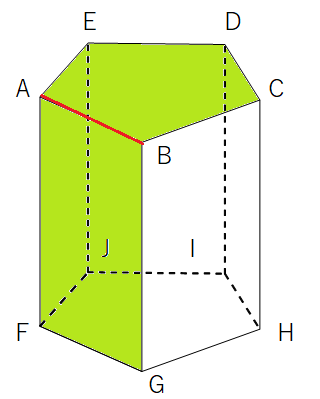
ねじれの位置を答える問題を解くときには、「同じ平面上にないかな?」と最終確認すると安心だね。
ここでひとつ疑問に思うかもしれない。
さっきの直方体の問題の場合、辺ABと同じ平面上にはないけれど、辺HGは「平行」だったよね。

実際にある平面だけに注目してしまうと、辺ABと辺HGは「同じ平面上にない」と思ってしまうよね。
でも、対角線上に平面があると想像してみて。
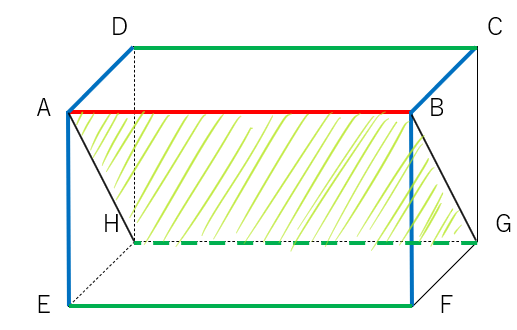
そう、実際にある平面以外にも、平面があると考えて「同じ平面上にあるか、ないか」を考えなくてはいけないんだね。
「ねじれの位置」の簡単な見つけ方
そんなの難しいよね。
でも、ちょっとオリジナルの方法を考えてみたよ。
こうやって「ねじれ」を見つけよう!「ローラー作戦」
辺ABを、AとBが長い棒を持って立っている二人組とイメージしてみよう。
そして、AとBが「いっせーのせ」とその棒を転がすんだ。
棒は、転がされた方向にそのままコロコロ転がって、方向を変えたりすることはないよ。
そのとき、「同じ平面上にあるのかないのか」を考えたい辺の上を、「その棒がすっかりきれいに辺すべての上を転がっていけるかどうか?」で考えてみて。
「辺にぶつかる」のではなくて、「辺の上をきれいにローラーするみたいに転がっていけるかどうか」だよ。方向転換してはいけないよ。
そうすると、きれいにローラーして転がっていけるのは、「交わる辺」か「平行の辺」だけのはず。
きれいにローラーしきれない辺は、「ねじれの位置にある」ということだよ。
三脚があって、四脚がない理由
カメラの三脚を見たことがあるかな?
足が3本あって、その上にカメラを設置し、安定して撮影できるようにする装置だよね。
三脚っていうのは文字通り、脚が3本あるんだけど、四脚というのはあまり見たことがないと思う。
なんとなく、四脚の方が安定しているように感じない?
だって、4本で支えているのだから。
けれど実際は三脚の方が安定しているんだよ。
四脚より三脚の方が安定している理由はなんでしょうか?
そこには数学的な理由があるんだ。
3点あれば、平面がただ1つに決まる
「一直線上にない3点があれば、平面がただ1つに決まる。」
たった3点を決めるだけで、平面が1つに決まるんだよ。わかりやすく表した図を見てみよう。
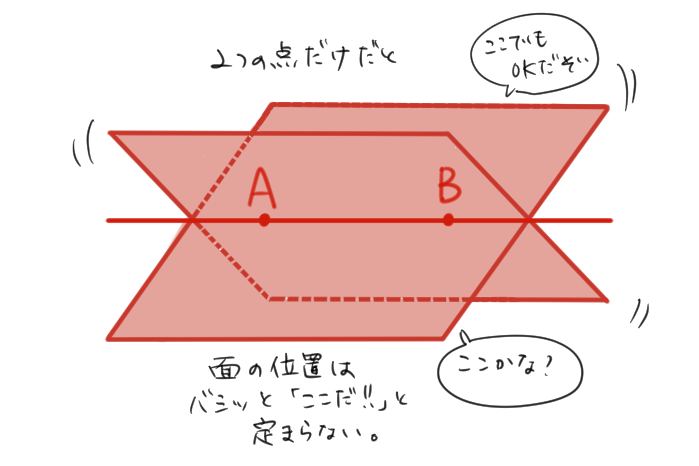
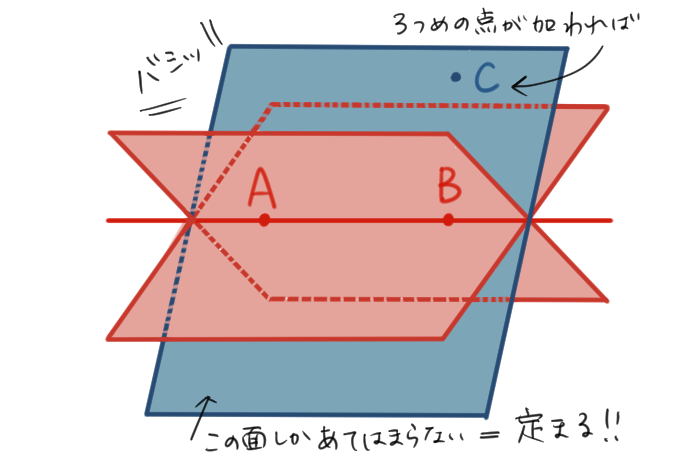
上の図では、AとBを通る平面はたくさん存在するけど3点AとBとCを通る平面はただ1つの平面(青色)だけだよね。
つまり、平面を1つに決めるには4つ目の点は必要ないってことになるんだ。
4点あると、不安定になることも
そうは言っても、どうせなら4点のほうがいいんじゃない?「大は小をかねる」って言うよね。と思うかもしれない。
実際には、4つ目の点があると逆に不安定になってしまうこともあるんだ。
三脚を使うところは基本的に外だよね。外ってことは地面が平面でないこともあるかもね。
三脚であれば、どこにおいても平面が一つに決まるんだけど、四脚だと、平面がいくつか存在して、「がたがた」揺れる状態になるんだよ。
下の図のような「でこぼこの地面」で使うとしようか。三脚の場合、必ず3本の脚が地面に接することになるよ。

倒れそうになったら1本の脚を調整するだけで、なんとかなるだけど、四脚はそうはいかない。
四脚だと1本が地面に接していない状態になって、「がたがた」揺れることになると思うよ。その理由は1本が短かったりすると平面が2つできあがってしまうから。

つまり、3点あれば平面がただ1つに決まり安定するということがイメージできるかな。
だから、世の中では、四脚より三脚の方が普及しているみたいだよ。
まとめ
- 平面と平面が交わったところにできる直線のことを「交線」という。
- 平行でなく、交わらない2つの直線を「ねじれの位置にある」という。
- 2つの直線の位置関係は、①交わる、②平行、③ねじれの位置の3つに必ず分類できる。
- 「交わる」「平行」の2つの直線は同じ平面上にある
- ねじれの位置の2つの直線は同じ平面上にない
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


