「おうぎ形の弧の長さと面積（平面図形）」をわかりやすく解説

中学数学「おうぎ形の孤の長さと面積」がどうしても理解できないという子にも分かるように、ひとつひとつのつまずきポイントを丁寧に解説していくよ！

「おうぎ形の弧の長さと面積（平面図形）」をわかりやすく解説のPDF（8枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

おうぎ形の弧の長さと面積
つまずきポイント

つまずきポイント

公式が複雑で、見ただけで挫折してしまう
公式が「どうしてそうなるのか」分からない
「おうぎ形」というだけで苦手意識がある

どんなに説明を受けても、とにかくピンとこないんだよ・・
どうせ難しそうと思って諦めちゃうんだ。

おうぎ形の弧の長さと面積を
身近な話に変えてみよう！

じゃあ、「おうぎ形」とか「弧」とかは一旦いったん忘れて、
身近な話で考えてみよう。

考えてみよう

太郎くんのクラスは、全部で40人の生徒がいるよ。

でも、インフルエンザでみんなお休みになって、２分の1の生徒だけが残ったんだ。

さて、何人の生徒が残っている？

そんなのカンタンだよ。
40人の半分の、20人でしょ。

計算で表すと、

40×\(\frac{1}{2}\)＝20

ということだね。

もちろん、これが2分の1でなくて、4分の1でも同じ考え方でいいよね。

これって、「円」と「おうぎ形」でも同じことなんだよ。

「全部で」というのが「円」のこと。
「残った生徒」が「おうぎ形」のことで考えてみて。

「円」＝「全部」

円というのは、「パーフェクトな状態」のことだよね。

ホールケーキとかピザで例えるなら、「食べる前」の状態。
つまり、全部揃った状態。満タン状態。

さっきのクラスの例えで言うと、「クラス全員の人数」。

「おうぎ形」＝「残ったもの」

おうぎ形というのは、パーフェクトだった円が欠けた状態。

※イメージしやすいように、このページでは　おうぎ形のことを「残った部分」という表現をするよ。

ケーキやピザでいうなら、何切れか食べられてしまった状態。
さっきの例えなら、「インフルエンザで何人かがお休みして、残った生徒」のことだね。

この、
「残ったもの」が実際どのくらいの量とか数があるのかは、「もとのパーフェクトな状態とくらべてどのくらいの割合残っているのか」でもとめられるよね。

クラスで考えた時のように、「もとの生徒の数」とくらべて「半分」残ったから、「残った生徒の数」は

40（全部）×　\(\frac{1}{2}\)（どのくらい残ったか）＝20（残った生徒の数）

になるんだよね。

おうぎ形も、

「円（全部）の時の円周」× 「残った割合」　＝　「おうぎ形（残った部分）」の円周」

というように求めることができるんだ。

説明だけだとピンとこないので、例題を解きながら説明していくよ。

おうぎ形の弧の長さと面積を
例題で考えてみよう

例題

次のおうぎ形の弧の長さと面積を求めなさい。

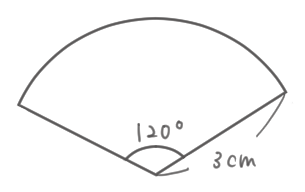
まずはもとの円（全部）の弧の長さと面積を求める。

クラスの生徒の例えだと、
「クラスの生徒は全部で40人」とあらかじめ分かっていたよね。

でも、このおうぎ形の「もともとの円の円周や面積はいくつなのか？」は
あらかじめ分かっていないね。

だから、まずは「もともとの円の弧の長さや面積はいくつなのか？」を求める必要があるんだ。

もともとの円が描いていないから、そんなの分からないよ。

くまごろう

ここで手がかりになるのが、おうぎ形にある「3㎝」という数字。
これって、実はもとの円の半径の部分なんだよね。

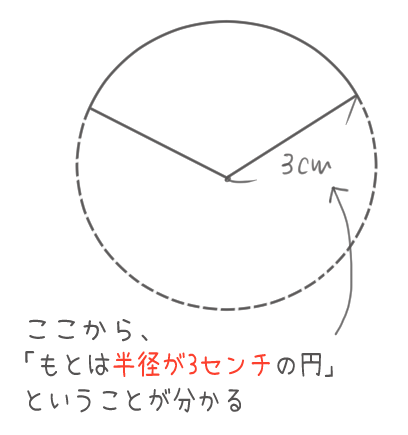
ということは、この半径を使えばもとの円の円周も面積も求めることができるね。

円周の求め方は　「直径（半径×2）×π」なので、

　3×2×π＝6πcm

つまり、もとの円だった時の円周は6πだね。

円の面積の求め方は　「半径×半径×π」なので、

　3×3×π＝9π㎠

ということになるね。

じゃあ、おうぎ形が、この円の半分だったとしたら？

円周も、面積も、もちろん半分になるよね。

だから円周なら6π㎝の半分の「3π㎝」になるし、
面積は「9π㎠の半分の「\(\frac{9}{2}\)π㎠」になるね。

4分の１だったら？
3分の2だったら？

とにかく、
もとの円の円周や面積を求めれば、
もとの円と比べておうぎ形がどのくらい残っているかによって、
おうぎ形の面積や円周も求めることができるんだね。

でも、おうぎ形が「もとの円」のどのくらい残っているのかは、どうやって分かるの？

それが分かるのがおうぎ形の「中心角」なんだ。

中心角を見れば
「おうぎ形がもとの円に対してどのくらい残っているか」が分かる！

おうぎ形が、もとの円にたいしてどのくらい残っているかの割合を求めるには、
円の中心核360度に対して、おうぎ形の中心角がどのくらいあるのかで求められるんだ。

例えば、ちょうど半分のおうぎ形の中心角は180度。

180度は、360度に対してどのくらいあるかの割合を求めると、

180÷360
＝\(\frac{180}{360}\)
＝\(\frac{1}{2}\)

90度の場合なら、
90÷360
＝\(\frac{90}{360}\)
＝\(\frac{1}{4}\)

こうやって、「おうぎ形の中心角」÷360をすれば、おうぎ形がどのくらい残っているのかの割合が求められるんだよ。

例題のおうぎ形の中心角は、120度だね。

そうすると、
120÷360
＝\(\frac{120}{360}\)
＝\(\frac{1}{3}\)

このおうぎ形は、もとの円に対して\(\frac{1}{3}\)残っているということだね。

求めた割合を、円周や面積にかける

そうしたら、あとは「もとの円だったときの円周や面積」に、求めた割合をかけてあげれば、おうぎ形の弧の長さや面積が求められるということだね。

もう一度、ひとつひとつ手順を表すと

①もとの円の円周や面積をもとめる

②おうぎ形が、もとの円に対して「どのくらい残っているか」をもとめる

③ ①に②をかける

例題で考えると、

①もとの円の円周は6π

②おうぎ形は、もとの円に対して\(\frac{1}{3}\)残っている。

③ ①に②をかけると、\(6π×\frac{1}{3}＝2π\)

というわけで、弧の長さは2π㎝だね。

くまごろう

同じように、おうぎ形の面積を求めると、3π㎠になるよ。

この作業をいっぺんに表したのが教科書の公式なんだよ。

弧の長さの公式：\(l＝2πr×\frac{a}{360}\)

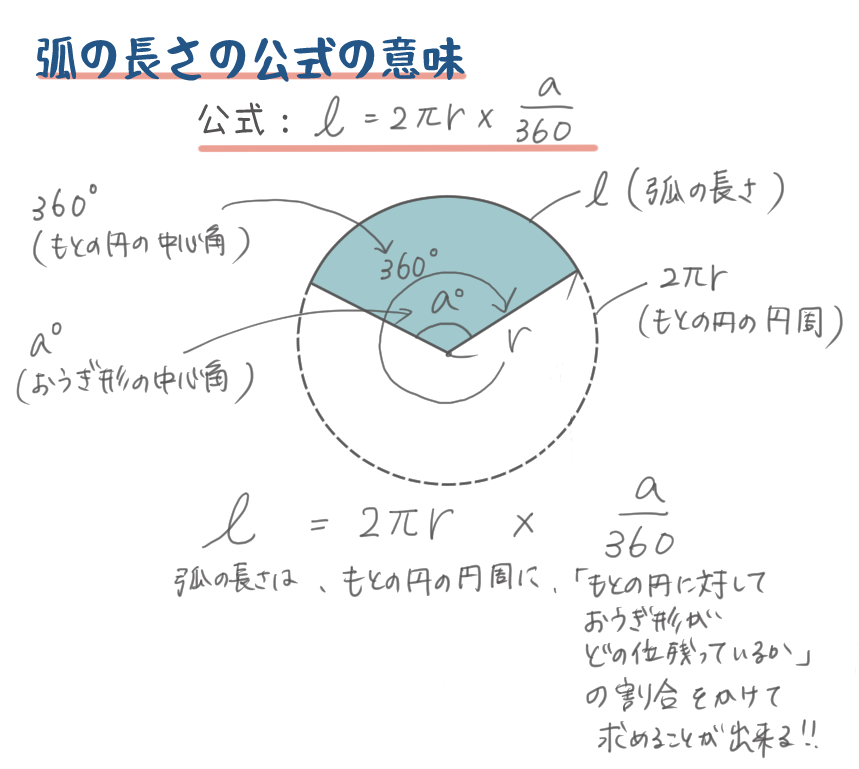
弧の長さの公式の意味のイラスト

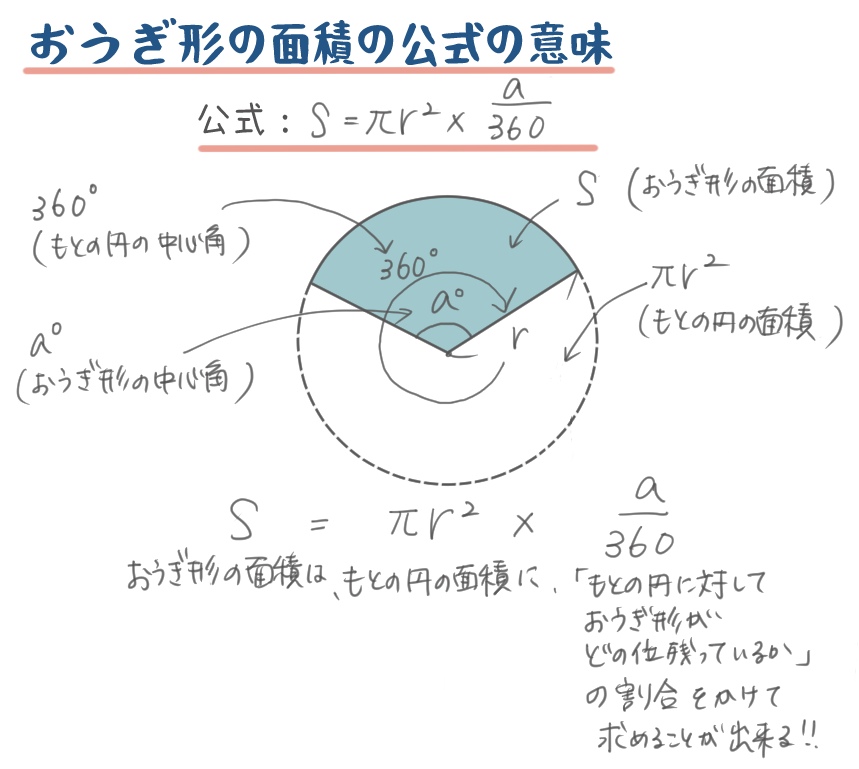
おうぎ形の面積の公式：\(s＝πr^2×\frac{a}{360}\)

おうぎ形の面積の公式の意味のイラスト

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。