垂線・垂直二等分線・角の二等分線の作図のやり方「基本の作図」
中学1年生の数学で学習する「基本の作図」。弧ABとは?弦とは?円の基本的な用語の説明と、垂線・垂直二等分線・角の二等分線の作図のやりかたをくわしく解説するよ。
円の基本的な用語を確認しよう!「弧」と「弦」とは?
コンパスを使って円を書いて、小学校で勉強した円の用語を確認しよう。
円の真ん中のことを「円の中心」、円の周りの長さのことを「円周」、円の中心と円周の1点を結んだ線を「半径」っていうんだったよね。
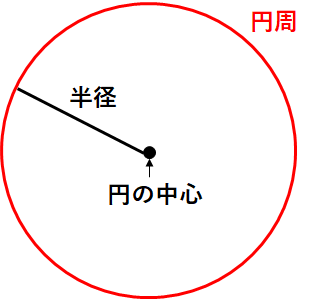
中学校では新しく2つの用語を覚えよう。次の図を見てみてね。
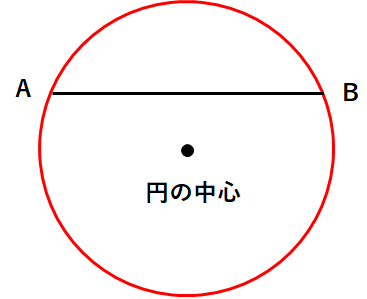
円周の上に、点Aと点Bをとって、2つの点を線分で結んだよ。
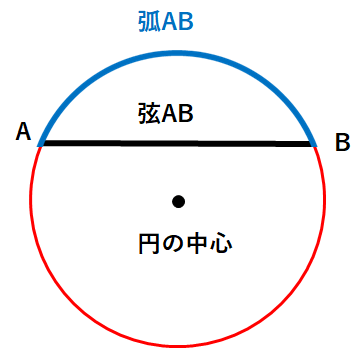
このとき、下の図で青い部分のことを「弧AB」、黒い部分のことを「弦AB」と呼ぶよ。弧ABのことを\( \overset{\frown}{AB} \)と表すよ。
※ちょっとややこしいけれど、赤い部分も「弧AB」だよ。
垂線の作図
垂線とは、ある直線に直角(90°)に交わる線のことだよ。垂線を作図する方法は2つあるから順番に紹介していくね。自分がやりやすい方法で作図しよう。
垂線の作図①
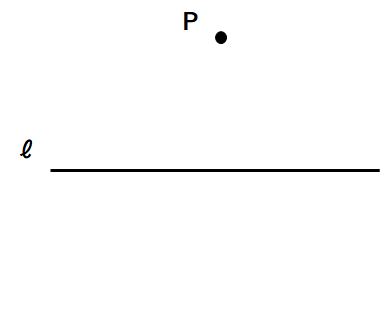
点Pを通る、ℓの垂線を作図しなさい。
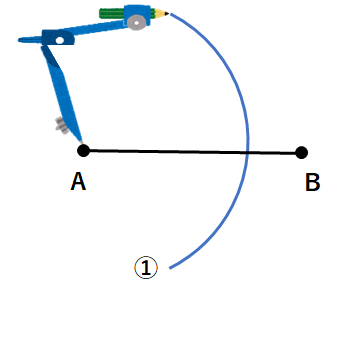
①点Pにコンパスの針をさして、適当に広げて、円を書き、ℓと交わる点ををA、Bとするよ。適当な半径の円でいいんだけど、ℓに2点で交わるようにコンパスを開いてね。
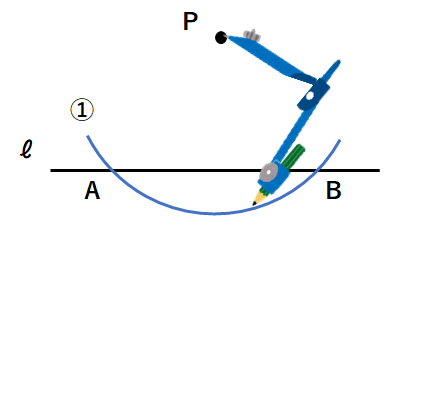
②点Aにコンパスの針をさして、①と同じ半径の円を書こう。
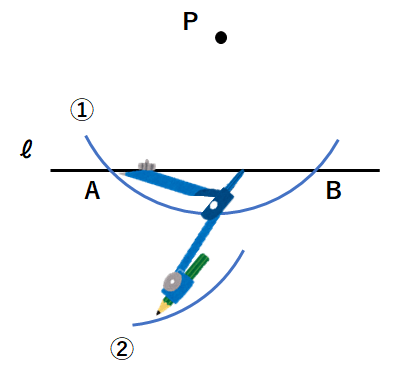
③点Bにコンパスの針をさして、①と同じ半径の円を書いて、②とその交わっているところをQとしよう。
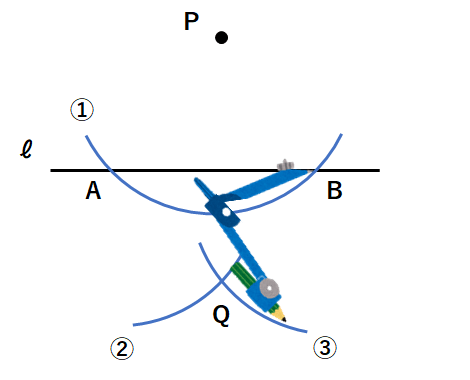
④点P、点Qを通る直線を引こう。下図の赤線が「点Pを通るℓの垂線」になるよ。当たり前だけどPQとℓは垂直になるから「PQ⊥ℓ」と表せるね。
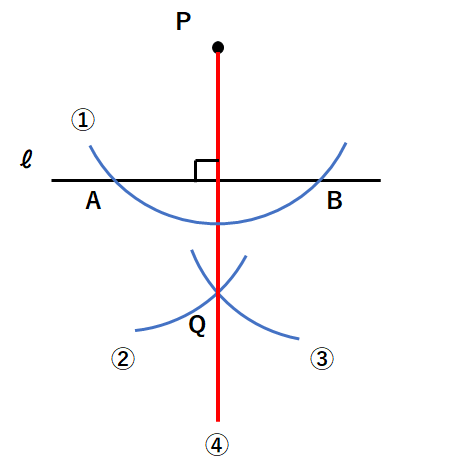
垂線の作図②
点Pを通る、ℓの垂線を作図しなさい。

①ℓ上に適当な2点A、Bをとって、点Aにコンパスの針をさして、点Pまで広げよう。下図のように円の一部を書こう。円は全部書かなくても大丈夫だよ。
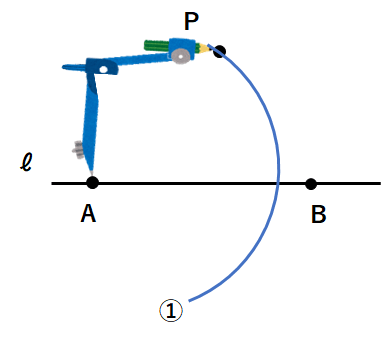
②点Bにコンパスの針をさして、点Pまで広げよう。下の図のように円の一部を書いて、①の円と交わっているところをQにしよう。
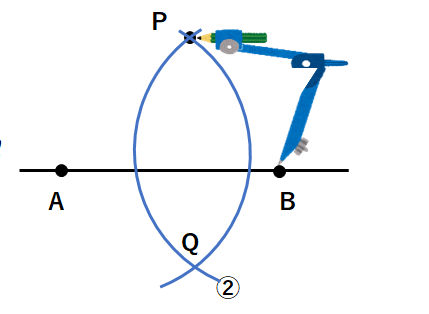
③点P、点Qを通る直線を引こう。下図の赤線が「点Pを通るℓの垂線」になるよ。
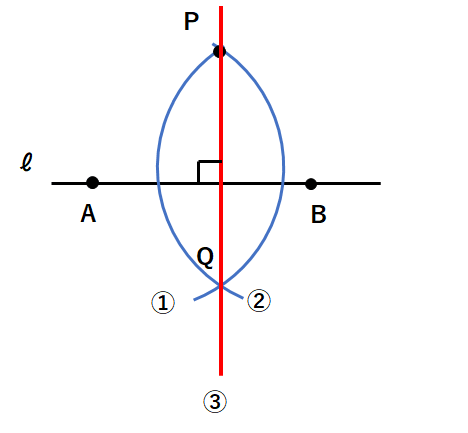
垂線の作図は2つのやり方があるけど、自分がやりやすい方を見つけてマスターしよう。
垂直二等分線の作図
垂直二等分線とは、ある線分を垂直に二等分する直線のことだよ。「垂線」と「二等分線」が合体した感じだね。
垂線の書き方の2つ目ができた人は余裕だと思うよ。
線分ABの垂直二等分線を作図しなさい。

①点Aにコンパスの針をさして、適当な半径の円を書こう。コンパスを広げる幅は適当でいいんだけど、線分ABの半分より長くしよう。
②点Bにコンパスの針をさして、①と同じ半径の円を書いて、①の円と交わる点をP、Qとしよう。コンパスの幅を変えちゃだめだよ。
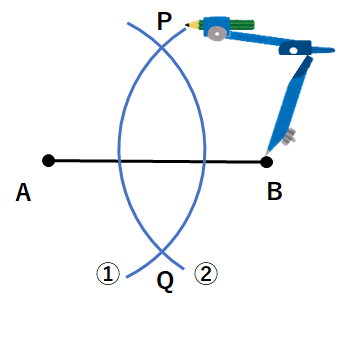
③2つの点P、点Qを通る直線を引こう。下の図で赤線が線分ABの垂直二等分線になっているよ。当たり前だけど、「AB⊥PQ」だね。
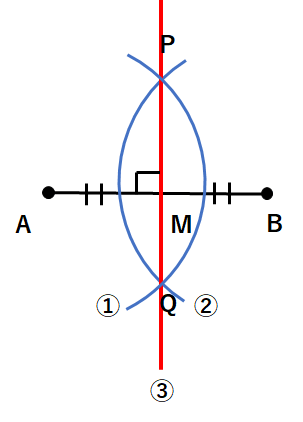
上図でPQとABが交わっている点をMとすると、AM=BMになっているよ。このとき点Mのことを線分ABの「中点」というよ。「真ん中の点」だから「中点」だね。
垂直二等分線の性質
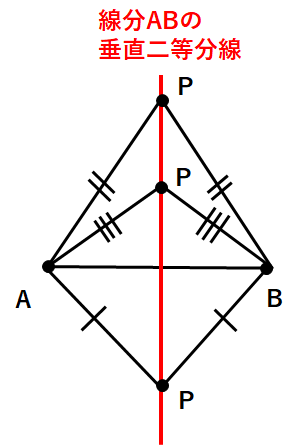
垂直二等分線にはすごく大切な性質があるんだよ。下図のように、垂直二等分線の上にある点と、点A、点Bとの距離は等しくなるよ。
もう少し簡単に言うと、垂直二等分線(赤線)の上であったら、必ずAP=BPになっているよ。
角の二等分線の作図
角の二等分線とは、ある角を二等分した線のことだよ。角の二等分線がかけるといろいろな角度を半分にすることができるんだ。
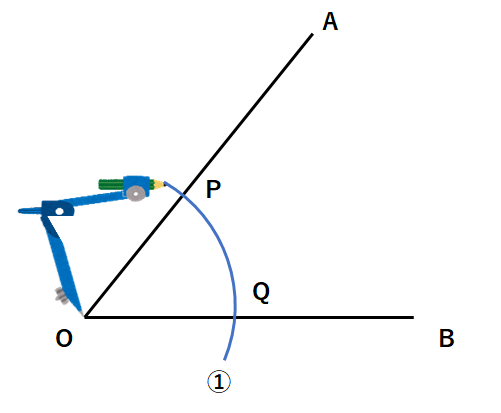
∠AOBの二等分線を作図しなさい。
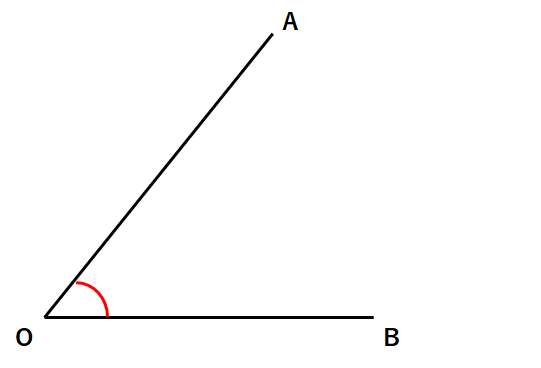
①点Oにコンパスの針をさして、適当な半径の円を書いて、OA、OBと交わる点をP、Qとしよう。
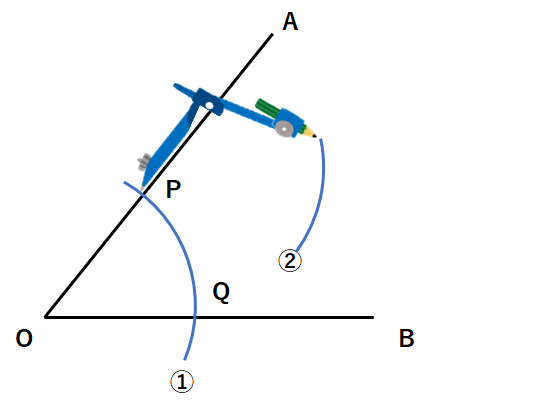
②点Pにコンパスの針をさして、①と同じ半径の円を書こう。
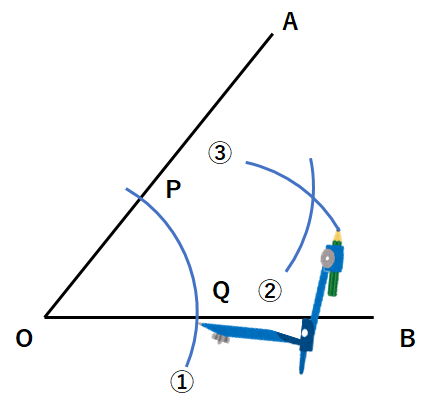
③点Qにコンパスの針をさして、①と同じ半径の円を書いて、②と交わる点をRとしよう。
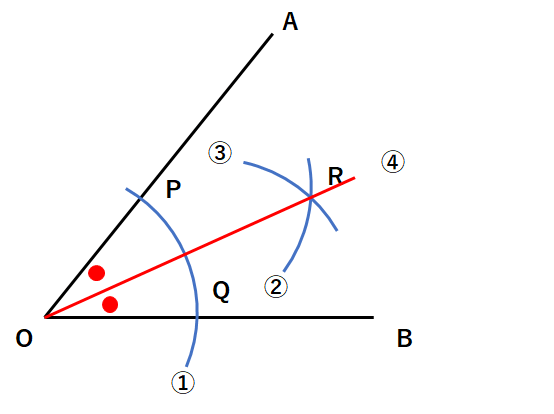
④半直線ORを引こう。下の図で赤線が∠AOBの二等分線だよ。角の二等分線だから、赤丸の角度の大きさは等しくなっているよ。
∠AOR=∠BORと表されるね。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


