一次方程式の効率的な解き方は?移項のやり方をわかりやすく解説!
方程式の効率の良い解き方
一次方程式の効率のよい解き方を紹介するね。この解き方をマスターすると、速く解を求めることができるよ。
効率の良い解き方をする理由
効率の良い解き方をすると、難しい方程式で効果を発揮するよ。
そもそも方程式を解くってどういうことだったかおさらいをしよう。
方程式を解くとは、等式を成り立たせるxの値を求めるってことだったよね。
例えば、
x+2=5という方程式だったら、xにいくつを代入したら成り立つかを考えていくと、x=3になるよね。
この程度の方程式であれば、簡単にxを求めることができるけど、次の方程式だったらどうだろう?
2x+3=x+4
この方程式を成り立たせるxを求めるのは大変だよね?
効率の良い解き方を知っていたら、簡単に解を求めることができるよ。
等式の性質を使って効率のよい解き方をする
一次方程式を効率的に解くためには、式の形をちょっと変える必要があるんだよ、
そして、式の形を変えるには、「等式の性質」を使えないといけないんだ。
なぜなら、式の形を変えるときに、変なことをすると「式が壊れちゃう」んだよ。
そうすると、間違った答えしか見つけられなくなっちゃうんだ。
「等式の性質」は、いわゆる「式を変えるときのルール」のようなもの。
「等式の性質」を理解していれば、式を壊さずに変えることができるんだよ。
では、等式の性質をもう一度確認してみよう。
等式の性質
等式は左辺・右辺の両方に同じ数を「たしても・ひいても・かけても・わっても」、等式は成り立ったまま。
なるほど、つまり式の形を変えるのに、左辺・右辺の両方に同じ数を「たす・ひく・かける・わる」をするのはOKということだね。
等式の性質を使って、効率的に方程式を解くためのステップを紹介するね。
そもそも方程式の最終的なゴールは「x=~~」という形になるってことは覚えておこう。
「x=~~」の形にするために、等式の性質を駆使して、式の形を変えていくよ。
イメージは、「文字は左辺に持っていく、数字は右辺に持っていく」こと。
つまり、文字と数字が混ざってしまっている式を、きれいに「文字は左側」「数字は右側」に整理してあげるんだ。
そのときに、等式の性質のルールを守りながら整理しようね、ということだね。
(例1)次の方程式3x+5=x-1を効率的に解きましょう。
ステップ1:項に下線を引く。文字の項を赤で、数字だけの項を青で引いたよ。(文字は左へ、数字は右へ整理するために、見分けやすいように色分けしたよ。)

ステップ2:左辺を文字の項だけにするために、両辺足したり、引いたりする
今回は、左辺に「+5」という項があるので、「+5」を消すために、両辺から5を引いたよ。
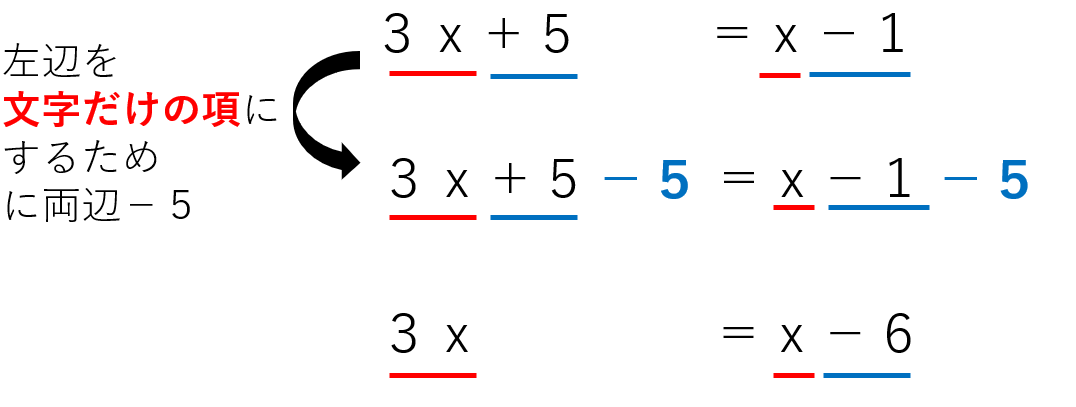
ステップ3:右辺を数字だけの項にするために、両辺足したり、引いたりする
今回は、右辺に「x」という項があるので、「x」を消すために、両辺からxを引いたよ。
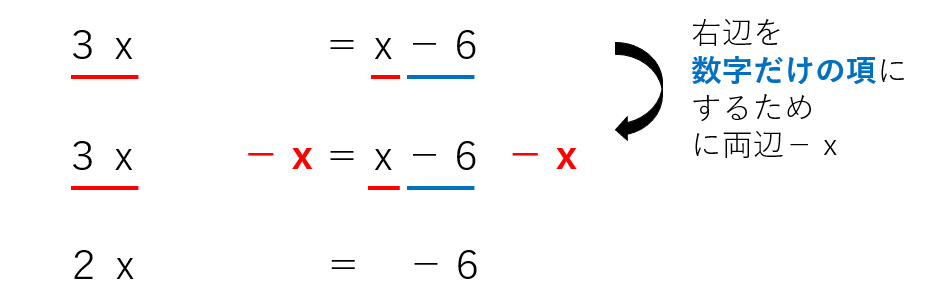
ステップ4:ここまでで「△x=・・・」のような形になっているはず。「x=~~」の形にするために、両辺かけたり、割ったりする。
「2x=-6」から「x=~~」にするには、両辺を2で割ったらいいね。
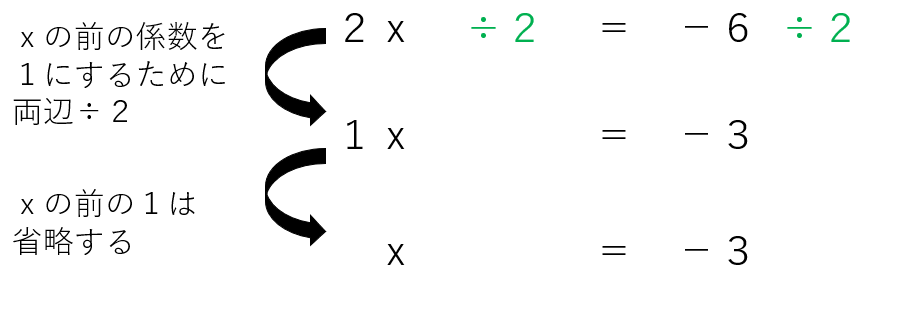
(例2)次の方程式2x-3=-x+3を効率的に解きましょう。
ステップ1:項に下線を引く。文字の項を赤で、数字だけの項を青で引いたよ。

ステップ2:左辺を文字の項だけにするために、両辺足したり、引いたりする
今回は、左辺に「-3」という項があるので、「-3」を消すために、両辺に3を足したよ。
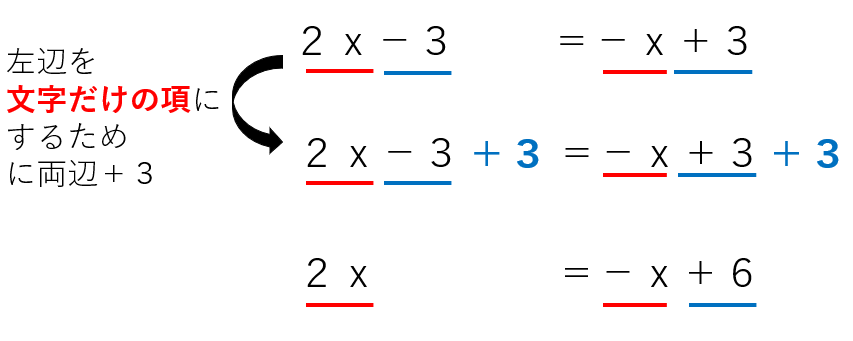
ステップ3:右辺を数字だけの項にするために、両辺足したり、引いたりする
今回は、右辺に「-x」という項があるので、「-x」を消すために、両辺にxを足したよ。
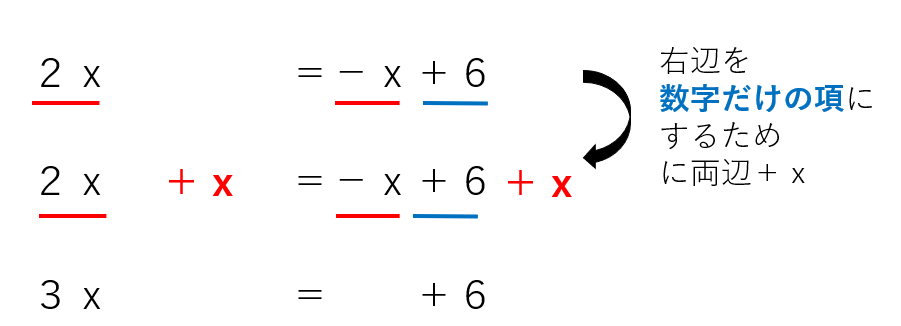
ステップ4:ここまでで「△x=・・・」のような形になっているはず。「x=~~」の形にするために、両辺かけたり、割ったりする。
「3x=+6」から「x=~~」にするには、両辺を3で割ったらいいね。
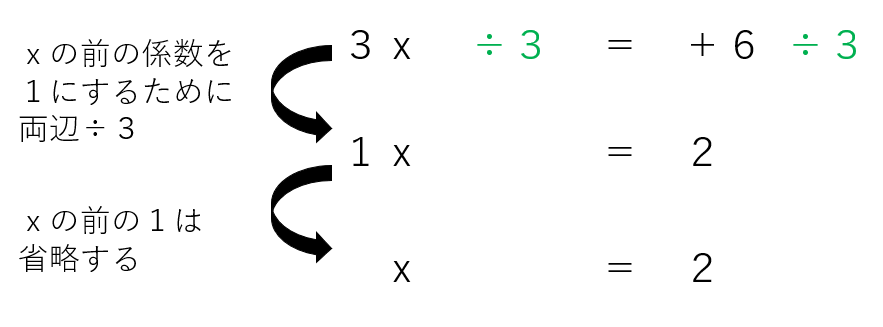
方程式を効率的に解くために、等式の性質のルールを守りながら式の形を変えて整理する方法はわかったかな?
とはいえ、両方の辺に数を足したりひいたり・・まだまだ大変だよね。
そこで、さらにスピードアップするチート技が「移項」なんだ。
移項とは
一次方程式をもっと効率的に解くための武器が「移項」。
「移項」を使うと、さっきのステップ2とステップ3を高速でできるようになるよ。
移項っていうのは、「左辺(または右辺)の項を、符号(+・-)を変えて、右辺(または左辺)へ移すこと」。
「項」を「移す」から、「移項」だね。
移項の練習
①方程式x+4=8 の「4」を左から右に移項すると、x=8-4になるよ。
②方程式3x-2=7の「-2」を左から右に移項すると、3x=7+2になるよ。
③方程式4=-2x+3の「-2x」を右から左に移項すると、4+2x=3になるよ。
移項して符号が変わる理由
でも、式を変えるとき、変なことをすると壊れちゃうって説明したよね。
項を勝手にもう片方の辺へ移動なんてさせて大丈夫なのか心配になるよね。
しかも、どうして符号も変わるのか、「??」という子も多いんじゃないかな。
ではなぜ、移項をしても大丈夫なのか、そして移項したら符号(+・-)が変わるのかを説明するね。
x+5=8という方程式を解いてみるよ。
xを求めるために、まず両辺から5を引くよね。
x+5 =8 ・・・①
x+5-5=8-5
x =8-5 ・・・②
x =3
解は求まったけど、ここで①と②の式を見比べてみよう。
x+5=8 ・・・①
x =8-5 ・・・②
両辺からおなじ「5」を引いた結果、結局のところ見た目的には左辺の「+5」が右辺に来て「-5」になっていることがわかるよね。
まるで項(+5)が左辺から右辺へ移動したみたいだよね。
これが移項のカラクリ。
だから「移項すると符号が変わる」という考え方をするよ。
つまり、移項は「両方の辺に足したり・引いたり」という部分をショートカットしているんだね。
移項でよくある間違い
移項でよくある間違いはこんな感じ
2x=6 で「2」を移項して、x=6-2みたいにすること。
移項っていうのは、項を移動させること。この方程式では、2xで固まり(項)になっているから、2だけ移項するなんてことはできないよ。
移項を使って方程式を解こう。
(例1)次の方程式3x+5=x-1を移項を使って解いてみよう。
ステップ1:項に下線を引く。文字の項を赤で、数字だけの項を青で引いたよ。

ステップ2、3:文字の項(赤線)は左辺に、数字の項(青線)は右辺に移項する。
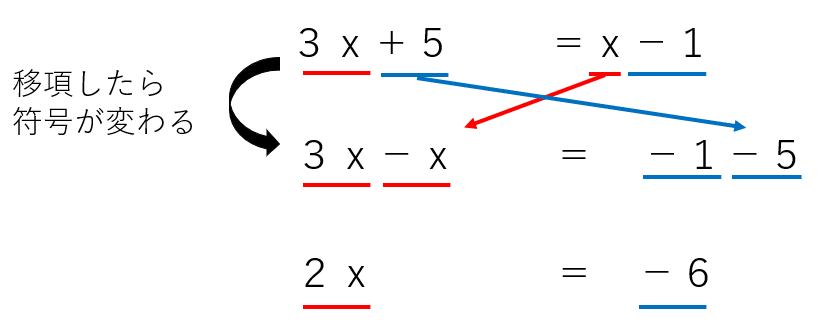
ステップ4:ここまでで「△x=・・・」のような形になっているはず。「x=~~」の形にするために、両辺かけたり、割ったりする。
「2x=-6」から「x=~~」にするには、両辺を2で割ったらいいね。
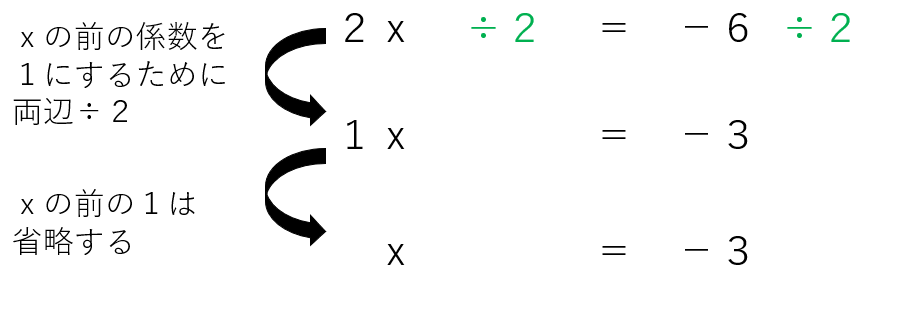
(例2)次の方程式2x-3=-x+3を移項を使って解きましょう。
ステップ1:項に下線を引く。文字の項を赤で、数字だけの項を青で引いたよ。

ステップ2、3:文字の項(赤線)は左辺に、数字の項(青線)は右辺に移項する。
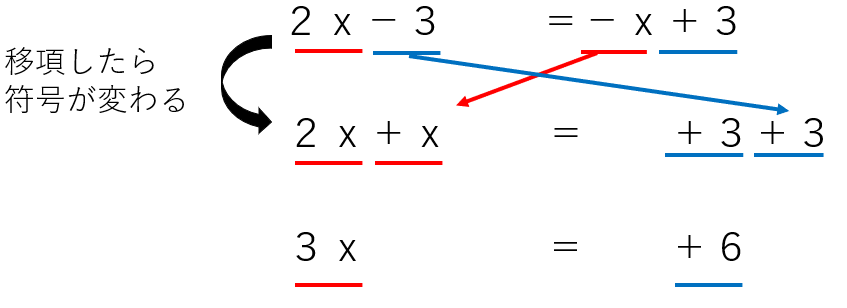
ステップ4:ここまでで「△x=・・・」のような形になっているはず。「x=~~」の形にするために、両辺かけたり、割ったりする。
「3x=+6」から「x=~~」にするには、両辺を3で割ったらいいね。
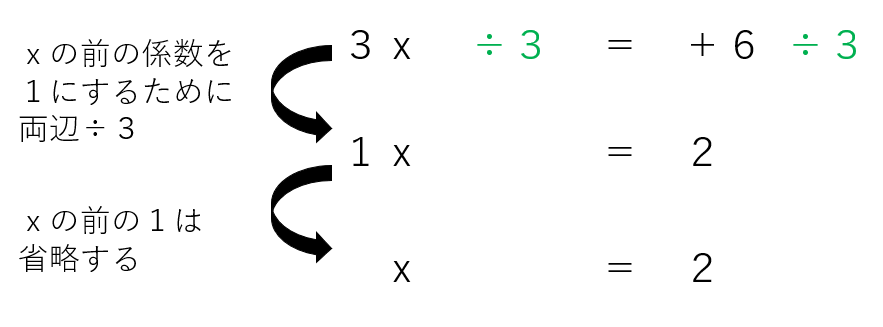
方程式を解く練習
方程式を移項や等式の性質を使って解いてみよう。
(1)x+3=9 (2)x-6=3
x =9-3 x =3+6
x =6 x =9
(3)3x-2=x+2
3x-x= +2+2 ←左辺は左辺同士、右辺は右辺同士で計算。
2x = 4
2x÷2 = 4÷2 ←「x=~~」にするために両辺を÷2
x = 2
(4)6x+1 =-2x+5
6x+2x= +5-1
8x = 4
8x÷8 = 4÷8 ←「x=~~」にするために両辺を÷8
x = \(\frac{4}{8}\) = \(\frac{1}{2}\)
まとめ
等式の性質を使って一次方程式を効率よく解く方法が分かったかな?
一次方程式を効率よく解くには、等式の性質と移項の知識が欠かせないから、しっかりできるようにしておこう。
今回学習したこと
- 等式の性質と移項を使うことで、一次方程式を効率よく解ける。
- 移項をすると符号が変わる。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



