「球の体積の求め方」球の体積の公式と覚え方をわかりやすく解説

中学数学で学習する「球の体積の求め方」について、球の体積はどのように求められるのか、球の体積の公式の考え方と語呂合わせなどの覚え方をわかりやすく解説するよ。

「球の体積の求め方」球の体積の公式と覚え方をわかりやすく解説のPDF（10枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

球の体積を調べてみよう

球の体積って、どうやったら求めることができるのかな。
体積といえば「底面×高さ」だけれど、球は全部が丸くて、底面といえるようなものはないし、高さなんていったら、それこそ「どこからどこ」なのか、想像もつかないよね。

この単元では、球の体積の求め方を考えるよ。
球の体積も、ちゃんと「球の体積を求める公式」というのがあって、それさえ覚えてしまえばこっちのもの。ある程度の問題は解けるようになるから安心してね。

ただ、そのまま「球の体積の公式」を丸暗記するのではなくて、「なんでその公式が成り立つのか？」を考えることで、少し発展的な問題も解けるようになるし、納得して公式を覚えることができると思うんだ。
なので、「球の体積を求める方法」を根本的なところから説明していくよ。

まず、球の体積を調べるために、「半径３cmの球がちょうど入る円柱」と「半径３cmの球の半球」について考えよう。

円柱の高さは、「球がちょうど入る円柱」なんだから、球の直径と同じ６cmだよ。

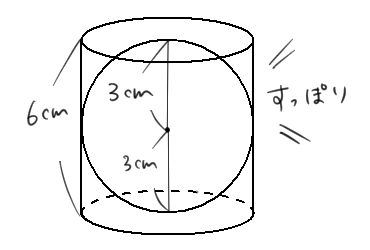
半球に水を入れて、円柱に移してみよう。何杯で円柱はいっぱいになるかな？

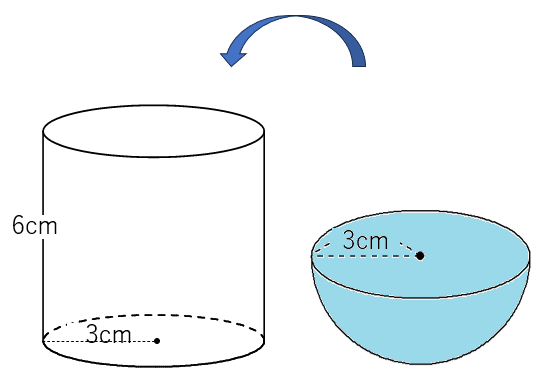
実際にやってみると、半球３杯でちょうど円柱１杯分になるんだよ。

たろう

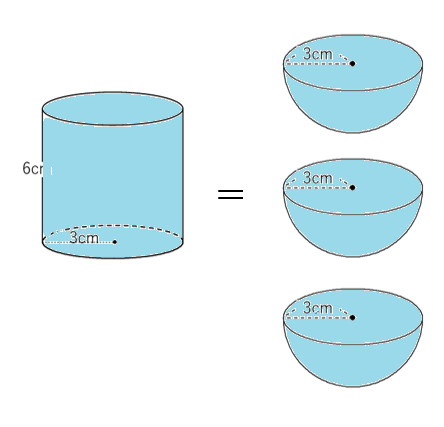
半球３つ分の体積が、円柱の体積とちょうどおなじなんだね！

球の体積と円柱の体積の関係

半球３つ分の体積と、その球がちょうど入る円柱の体積が同じという関係であることがわかったね。
では、その関係から、「球の体積」と「円柱の体積」の関係を考えてみよう。

まず「球の体積」は、「半球を２つ合体」させればいいよね。

円柱に入っている水の量は、半球が３つ分だったね。ということは、「半球が２つ分」の「球の体積」は、円柱に入っている水の「\(\frac{２}{３}\)」になるよね。

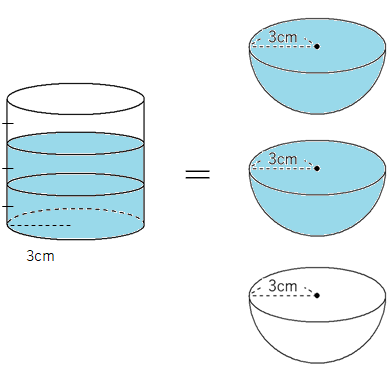
つまり、「球の体積」は「円柱の体積の\(\frac{２}{３}\)」になるんだね。

球の体積と円柱の体積の関係

球の体積は、その球がちょうど入る円柱の体積の\(\frac{２}{３}\)である。

球の体積の求め方（球の体積の公式）

さっきわかった「球の体積と円柱の体積の関係」を使って球の体積の公式を求めてみよう。

さっきは「半径は３cm」として考えていたけれど、公式を考えるために、半径は「ｒ」とするよ。

まず、円柱の体積を求めて、それを\(\frac{２}{３}\)倍して球の体積を計算しよう。

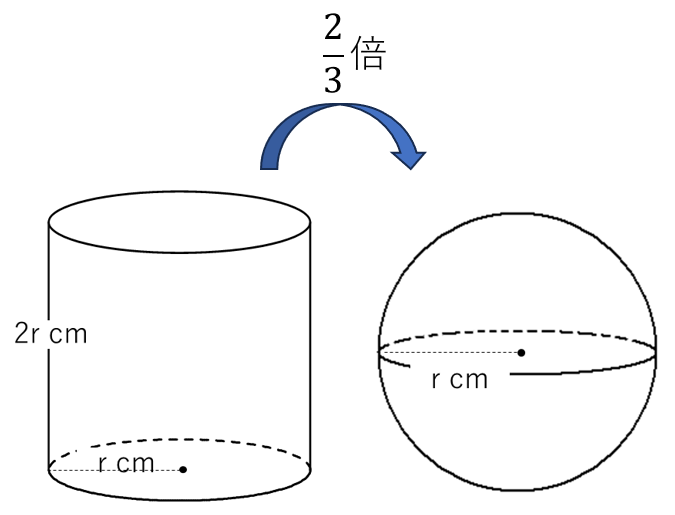
「半径ｒcmの球がちょうど入る円柱」の底面の半径はｒcmで、高さは２ｒcmになるね。
なので、円柱の体積は

（底面積）×（高さ）　←円柱の体積を求める公式

＝（ｒ×ｒ×π）×（２ｒ）

＝２πｒ^３

円柱の体積は２πｒ^３ (cm³)と求めることができたね。

さて、球の体積はさっきわかったとおり、次のような性質があるので、円柱の体積を\(\frac{２}{３}\)倍するよ。

球の体積は、その球がちょうど入る円柱の体積の\(\frac{２}{３}\)である。

（円柱の体積）×\(\frac{２}{３}\)

＝２πｒ^３×\(\frac{２}{３}\)

＝\(\frac{４πr^3}{３}\)

球の体積が\(\frac{４πr^3}{３}\) (cm³)と求めることができたね。

この「\(\frac{４πr^3}{３}\)」が球の体積の公式なんだ。

球の体積の公式

\(\frac{４πr^3}{３}\)

この公式さえ知っておけば、だいたいの球の体積を求める問題は解けると思うよ。
さっそくチャレンジしてみよう。

球の体積を求める問題

次の球の体積を求めなさい。

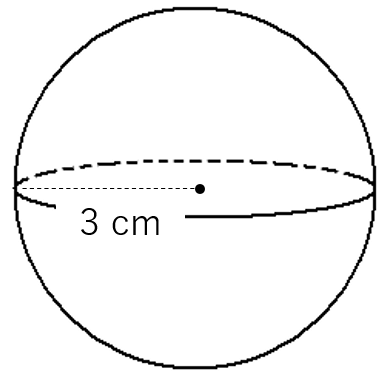
球の体積を求める公式は\(\frac{４πr^3}{３}\)だったよね。今回の問題では、半径ｒ＝３なので、次のようになるよ。

\(\frac{４πr^3}{３}\)

＝\(\frac{４π}{３}\)×ｒ^３　　　←ｒ＝３を代入

＝\(\frac{４π}{３}\)×３^３　　　←３^３を計算する

＝\(\frac{４π}{３}\)×２７

＝３６π

球の体積は３６π (cm³)と求めることができたね。

球の体積はなぜ３分の４なの？

球の体積の公式の「３分の４」という数字について、次のようにも説明することができるんだ。
ただ、かなり複雑で、教科書でいうと「発展」のところに載っているレベルなので、「こんな考え方もあるんだな」という感じで読んでみてね。

たとえば、球の表面を細かい三角形に分けたとしてみよう。
そうすると、その三角形ひとつひとつは、「底面が三角形で高さｒcm（球の半径）」の「三角錐」が集まって球ができあがることがわかるかな？

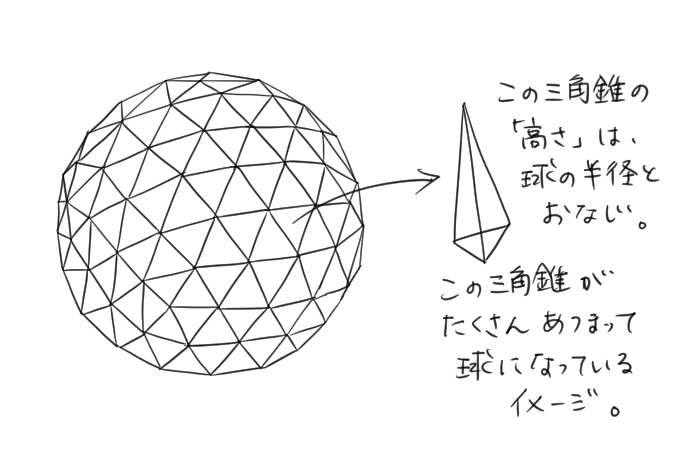
ここで、１つの三角錐の底面積をS₁、高さをｒとすると、１つの三角錐の体積は

（底面積）×（高さ）×\(\frac{１}{３}\)　　←三角錐の体積の公式

＝S₁×ｒ×\(\frac{１}{３}\)　

＝\(\frac{１}{３}\)S₁ｒ

三角錐がいくつも集まって球が出来上がっているから、球の体積「V」は、これら全部の三角錐の体積が合わさったものと同じだよね。
それは、こんな感じで表すことができるよ。

V＝\(\frac{１}{３}\)S₁ｒ＋\(\frac{１}{３}\)S₂ｒ＋\(\frac{１}{３}\)S₃ｒ＋・・・

たとえば、球の表面を１００個の三角形に分けたとしたら、「ｓ_１」から「ｓ_１００」までの三角錐の体積をたしたものと同じになるということだね。

表面全部の三角錐の底面を合計したものって、実は「球の表面積」と同じだよね。だって、三角錐の底面はもともと「球の表面を三角形に分けた」んだから。

ということは、上の式はつぎのように言い換えることができるね。

＝\(\frac{１}{３}\)Sｒ　　　　←「S」は球の表面積

球の表面積は次の単元で学習するんだけれど、「S＝４πｒ^２」で求めることができるんだ。
なので、

V＝\(\frac{１}{３}\)Sｒ

＝\(\frac{１}{３}\)×４πｒ^２×ｒ

＝\(\frac{４πr^3}{３}\)

これで、球の体積が\(\frac{４πr^3}{３}\)と表されることが確認できたね。
三角錐の体積の\(\frac{１}{３}\)と球の表面積の「４」πｒ^２が合体して、３分の４になっているということがわかったかな。

球の体積の覚え方（語呂合わせ）

球の体積の公式「\(\frac{４πr^3}{３}\)」だけれど、少しややこしいよね。
実は語呂合わせで覚えることができるので、紹介するよ。

球の体積の公式の語呂合わせ

みのうえに　しんぱい　あーるさんじょう
　（３）　　　（４π）　　　（ｒ^３）
みのうえに　しんぱい　あーるさ
　（３）　　　（４π）　　（ｒ^３）

くまごろう

「急な退席をする同級生の身の上を心配する」というイメージなんかどうかな

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。