「比例のグラフ」の書き方をわかりやすく解説(x軸・y軸とは)
中学1年生の数学で学習する「比例のグラフの書き方」をわかりやすく解説するよ。
グラフを書くのに必要な「x軸・y軸」とはなにか、「原点」とはなにか、比例の表からのグラフの書き方、比例の式からのグラフの書き方をくわしく説明するよ。
比例のグラフの書き方を確認しよう
どうして比例のグラフの書き方を学習するの?
これまでたくさん比例の学習をしてきて、比例って、xとyがどういう関係のことをいうのかが分かってきたね。
今度は、「比例のグラフ」の書き方を学習するよ。
グラフは、関数(xとyという2つの数がどういう関係か)を「見てすぐに分かりやすいように」したもの。
みんなも、たとえばアンケートの結果を確認するときに、ただ数字で「〇〇70%で、✖✖は30%でした」って言われるより、円グラフとかで描いてあるほうがぱっと見て「〇〇のほうが✖✖より明らかに多い!」って分かりやすくなったりするよね。
比例の関係も、「xがこれだけ増えると、yもこれだけ増える」というのがグラフになっているともっと分かりやすくなるんだ。
より分かりやすく伝えるために、そしてグラフからよりたくさんのことを読み取れるようになるために、「比例のグラフ」の書き方を勉強するんだね。
比例のグラフを書けるようになるには、まず「x軸・y軸・原点・座標」という言葉の意味を知らないとなので、言葉の説明をしてから、実際にグラフを書く練習をしていこう。
x軸・y軸(座標軸)とは
グラフを書くときに絶対に知らなくてはいけないのが、x軸とy軸。
今までは数直線といったら、次のような横軸だけだったけど、比例のグラフでは縦軸も混ざってくるよ。

なぜなら、そう。比例は、「xとyの2つの数の関係」だからだね。
数直線がひとつだけだと、2つの数の関係は表せないんだ。
比例のグラフでは、「xの数字がいくつかを表す直線(横向き)」と、「yの数字がいくつかを表す直線(縦向き)」の2つの数直線を使うんだよ。
この「xを表す横軸(横向き)の数直線」のことを「x軸」、
「yを表す縦軸(縦向き)の数直線」のことを「y軸」というよ。
そして、x軸とy軸のことを合わせて「座標軸」と呼ぶよ。
※「座標」という言葉は、あとでまたくわしく説明するので安心してね。
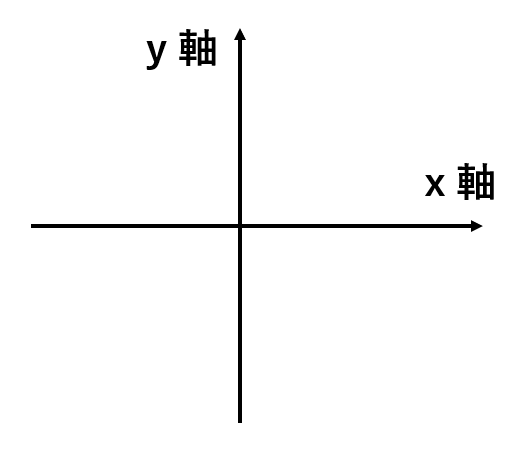
数直線の学習でもやったと思うけど、横の数直線(x軸)では、右に行けばいくほど、数字が大きくなったね。
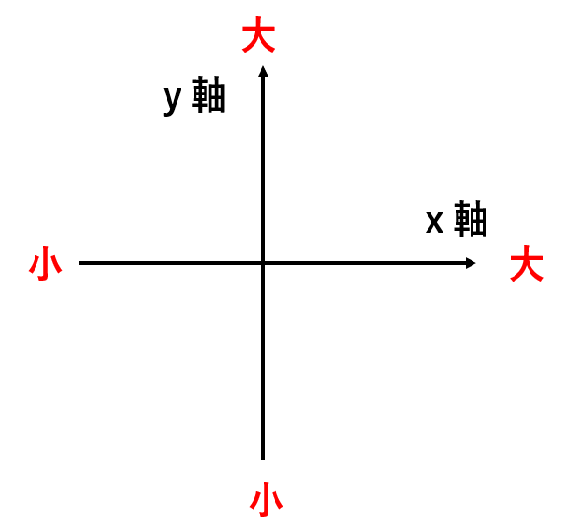
同じように縦の数直線(y軸)は、上に行けばいくほど、数字が大きくなるよ。
イメージにすると次のような感じ。
原点とは
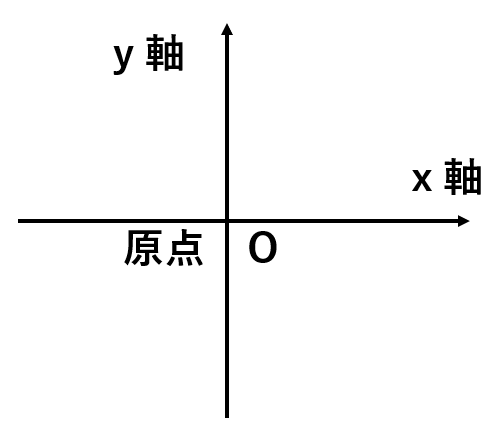
「原点」とは、「x軸」と「y軸」が交わるところのことだよ。
原点はいわば「スタート地点」。
x軸なら原点から右側が正の数、左側が負の数になっているよ。
y軸なら原点から上側が正の数、下側が負の数になっているよ。
原点はアルファベットを使って「O(オー)」で表すよ。
「0(ゼロ)」ではないので、覚えておこうね。
英語の「オリジン(origin)」の頭文字なんだ。
「比例のグラフ」ポイント
- 横の数直線のことを「x軸」といい、右に行けばいくほど数値は「大きく」なる
- 横の数直線のことを「x軸」といい、右に行けばいくほど数値は「大きく」なる
- x軸とy軸両方合わせて「座標軸」と呼ぶ
- x軸とy軸が交わるところを「原点」と呼ぶ
- x軸は原点から右が正の数、左が負の数
- y軸は原点から上が正の数、下が負の数
x座標・y座標とは
「x座標」と「y座標」とは何かというと、簡単に言ってしまうと住所みたいイメージ。
比例のグラフでは、xとyの数値が決まると、それをグラフ上に点で表すんだけれど、その点の住所をはっきりさせるのが「座標」なんだ。
例えば、下の点を考えてみよう。この点の場所を説明するとき、ルールがないと、「ちょっと右らへん」とか「上から3こ目で右から2こ目」と言った感じで、人によってみんな違う説明になっちゃうよね。
では、「座標」はどういう仕組みなのか説明するよ。
座標の仕組みと、読み取る練習①
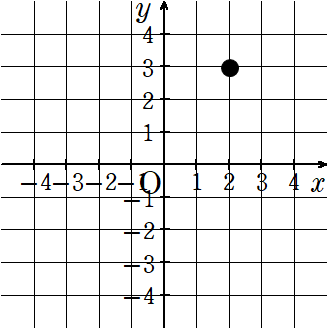
この点の座標(住所)はどうやって表すのかな?
下の①~③の順番で座標を求めるよ。
①横の数直線(x軸)の目盛りを見ると「2」
→x座標が「2」
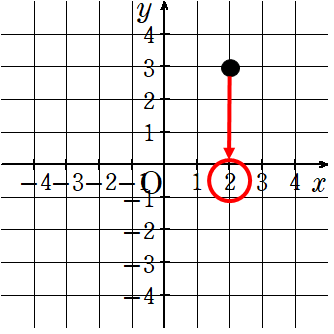
②縦の数直線(y軸)の目盛りを見ると「3」
→y座標が「3」
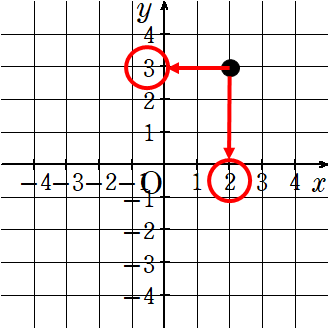
③座標は( xの座標,yの座標 )というように表すので、
x座標が2で、y座標が3の場合は(2,3)と表す。
座標を読み取る練習②
同じやり方で下の点の座標を求めてみよう。
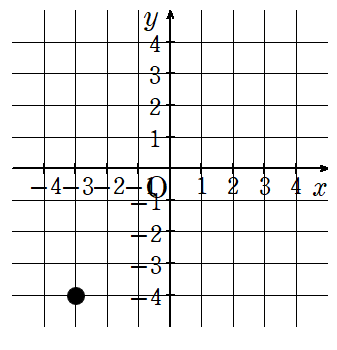
下の①~③の順番で座標を求めるよ。
①横の数直線(x軸)の目盛りを見ると「-3」
→x座標が「-3」
②縦の数直線(y軸)の目盛りを見ると「-4」
→y座標が「-4」
③座標は(-3,-4)と表す
座標を読み取る練習③
次のA~Eの座標を読み取りましょう。
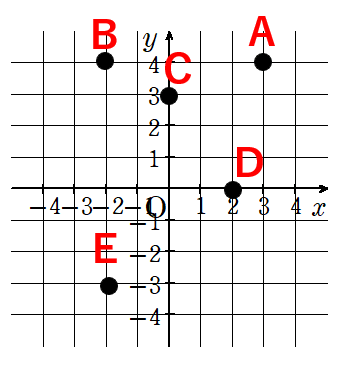
A(3,4)
B(-2,4)
C(0,3)
D(2,0)
E(-2,-3)
座標や軸などの言葉の意味はわかったかな?
ではここから今回の本題、グラフの書き方を説明するよ。
表から比例のグラフを書くときに一番大切なことは座標を理解できているかだから、わからなかったら前にもどって復習をしよう。
表から比例のグラフを書いてみよう
次の表はxとyが比例の関係であることを表しているよ。
だってxが2倍、3倍になると、yも2倍、3倍になっているからね。
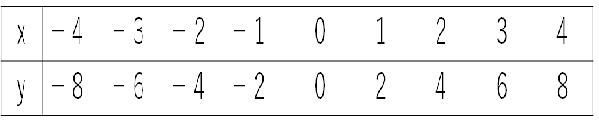
では、この表から比例のグラフを書いてみよう。
表からグラフを書くときは、表を「縦のかたまり」で見ていくよ。
たとえば、「xが1のとき、yは2」になっているね。
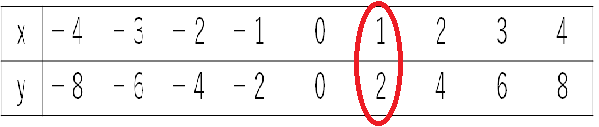
ということは、この比例をグラフにすると、xが1のとき、yは2の場所に点がくるということなんだ。
座標(住所)で表すと、(1,2)になるね。
こうやって、表にあるxとyの数字を、縦のかたまりごとに全部座標で表してみるよ。
x=1のとき、y=2
→座標で表したら(1,2)
x=2のとき、y=4
→座標で表したら(2,4)
x=3のとき、y=6
→座標で表したら(3,6)
x=4のとき、y=8
→座標で表したら(4,8)
x=-1のとき、y=-2
→座標で表したら(-1,-2)
x=-2のとき、y=-4
→座標で表したら(-2,-4)
x=-3のとき、y=-6
→座標で表したら(-3,-6)
x=-4のとき、y=-8
→座標で表したら(-4,-8)
このことからグラフは次の点を通ることがわかるね。
(1,2)(2,4)(3,6)(4,8)(-1,-2)(-2,-4)(-3,-6)(-4,-8)
これらの点をグラフ上にとってみると次のようになるよ。
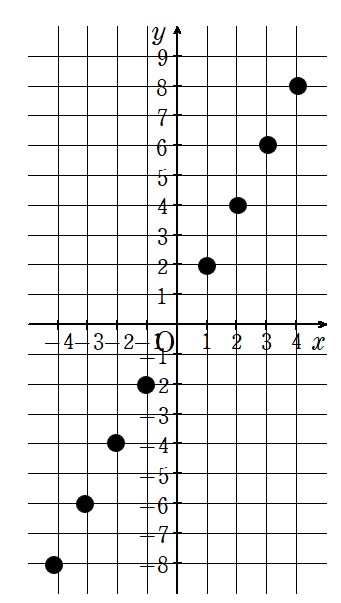
これらの点を定規で結ぼう。
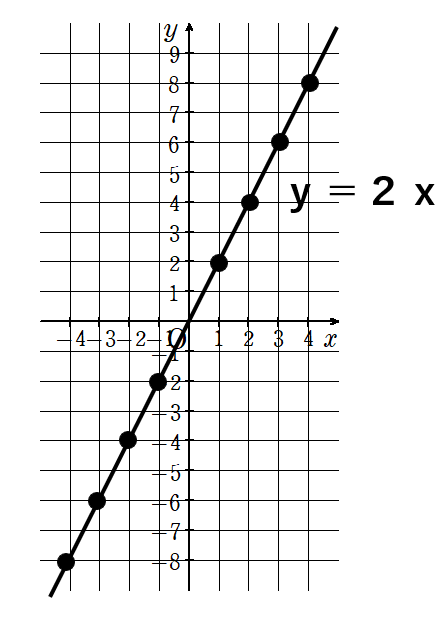
これで、表から比例のグラフを書くことができたね。
すべての点をつなげると、直線になったね。
そう、比例のグラフは、「直線」になるんだ。
そしてその直線は、かならず「原点」を通るんだ。
この2つは、比例のグラフの特徴なので、覚えておいてね。
ところで、表から比例のグラフを書くのに、今回みたいに全部の点を座標にひとつひとつ書きこむのは、さすがに大変だよね。
そんな時、じつはこの「比例のグラフの特徴」が役に立つんだ。
比例のグラフはかならず「直線」になって、かならず「原点」を通るということは、ひとつだけ点を座標に書きこめば、あとはその点と原点をつなぐ直線を定規で引けば、グラフが書けてしまうんだよ。
表から比例のグラフを書く手順
- 表を縦にみて、xとyの値を読み取る。
例:x=1のときy=2 - 読み取ったxとyの値をもとに座標に点を書きこむ。
例:(1,2)に点を書きこむ - 書きこんだ点と、原点を通る直線を定規で引く。
例:(1,2)と原点(0,0)を通る直線を定規で引く
式から比例のグラフを書いてみよう
それでは、今度は「比例の式」から比例のグラフを書く方法を説明するよ。
式から比例のグラフを書く方法
式から比例のグラフを書くには、「比例定数a」に注目しよう。
比例定数ってなんだっけ?
比例定数っていうのは、比例の式y=axの「a」のことだよ。
比例のグラフでは、ある点から右に1増えたら、上に比例定数だけ増えるという特徴があるよ。
「右に1増えたら、上に比例定数の分だけ増える」とは
「右に1増える」というのは、横軸はx軸だから、「xの値が1増える」ということになるよね。
そして「上に増える」というのは、縦軸の「yの値が増える」ということだよね。
比例の式はy=axだから、xが1増えるたびに、yがa増える計算になるのも分かるかな?
なぜなら、x=1のとき、yはaだよね。
x=2のとき、yは2a(xが1増えると、yはa増える)
x=3のとき、yは3a(xが1増えると、yはa増える)
だから、「右(x軸)に1増えると、上(y軸)に比例定数の分だけ増える」というわけだよ。
この特徴を使うと、グラフがとてもかんたんに書けるんだ。
でも、どこからスタートすればいいだろう。
だって、まだどんな形のグラフかが分からないんだから、どこの位置を通るかなんてわからないよね。
だけど、「比例の式」が必ず通る場所が1つだけあったのを思い出してみて。
そう、「原点」だよ。
なので、書くスタート位置は原点にするんだ。
y=3xのグラフを書いてみよう
①比例定数を確認しよう。比例定数は「3」だよね。
②比例定数が3だから、「右に1増えたら、上に「3」だけ増える」ことになる。
③原点をスタートにして、右に1、上に「3」行ったところに点を打つ。
④③でとった点から、さらに右に1、上に「3」行ったところに点を打つ。
⑤同じような感じで点を打っていく。
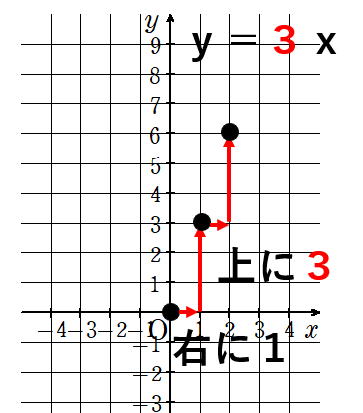
あとはこの点をつなげばいいんだね。
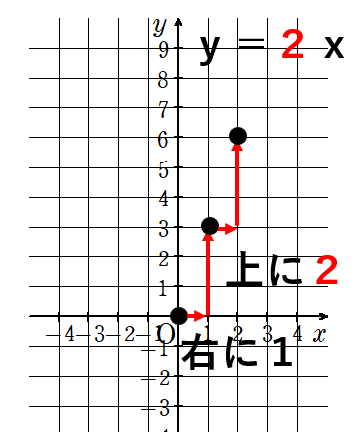
y=2xのグラフを書いてみよう
①比例定数は「2」だよね。
②右に1つ増えたら、上に「2」だけ増えるよね。
③原点スタートで、右に1、上に「2」行ったところに点を打つ。
④③でとった点から、右に1、上に「2」行ったところに点を打つ。
⑤同じような感じで点を打っていく。
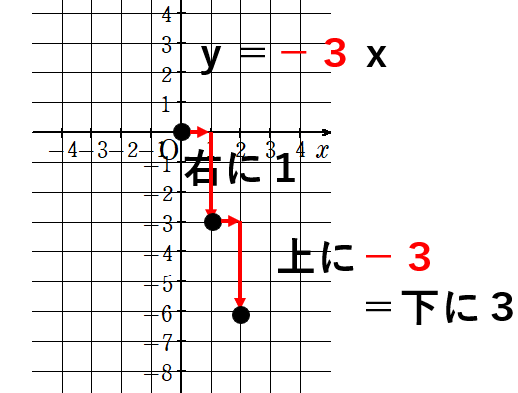
y=-3xのグラフを書いてみよう
①比例定数は「-3」だよね。
②右に1つ増えたら、上に「-3」だけ増える。
③原点スタートで、右に1、上に「-3」行ったところに点を打つ。
上に-3ということは、下に3行くという意味になるよ。
④③でとった点から、右に1、上に「-3」行ったところに点を打つ。
⑤同じような感じで点を打っていく。
式から比例のグラフを書くポイント
- 比例定数に注目する
- 原点から、右に1行ったとき、上に比例定数だけ行ったところに点を打つ。
比例の性質を確認しよう
比例の性質を確認する前に、比例のグラフを4つ書いてみよう。どんなことに気づくかな。
(問)次のグラフを書きなさい。
(1)y=4x (2)y=6x (3)y=-4x (4)y=-6x
答えは次の通りだよ。できたかな。
(1)y=4x(下の左側のグラフ)
(2)y=6x(下の右側のグラフ)
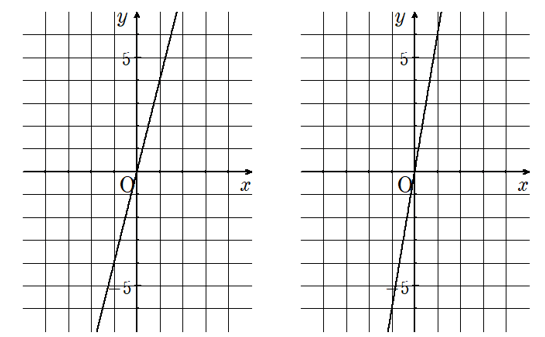
(3)y=-4x(下の左側のグラフ)
(4)y=-6x(下の右側のグラフ)
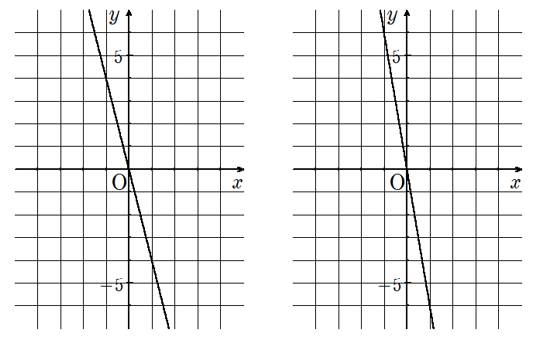
これらの4つのグラフを見て、比例のグラフのどんな性質に気が付くかな?
1つ目は必ず原点を通ること。これはもう説明したね。
2つ目は「比例定数の正負」で、グラフの形(向き)が変わってくること。
(1)(2)は比例定数が正になっていて、グラフの形は「右上がり」だね。
一方(3)(4)は比例定数が負になっていて、グラフの形は「右下がり」だね。
この性質も、かならず覚えておいてね。
比例定数が分数の式のグラフの書き方
y=2xやy=-3xのようなグラフは書けるようになったね。
では、y=\(\frac{1}{3}\)xのグラフはどう書けばいいかかわかるかな?
さっきと同じように考えると、
比例定数は\(\frac{1}{3}\)だから、原点から右に1、上に\(\frac{1}{3}\)行ったところに点を打てばいいことになるよね。
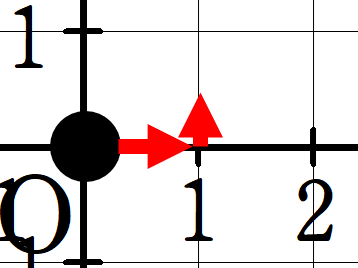
でも上に\(\frac{1}{3}\)といっても、目盛りがないから点が打てないよ。
比例定数が分数の時は次のやり方でやるといいよ。
比例定数が分数の場合は、分母の分、右に動いて、分子の分、上に動く
右に1だと、上に\(\frac{1}{3}\)になる(打てない)
右に2だったら、上に\(\frac{1}{3}\)×2=\(\frac{2}{3}\)になる(打てない)
右に3だったら、上に\(\frac{1}{3}\)×3=1(これなら打てる!)
原点から右に3、上に1行ったところに点を打っていけばいいね。
では、比例定数が分数の問題に挑戦してみよう。
y=\(\frac{3}{4}\)xのグラフを書こう
比例定数は\(\frac{3}{4}\)だから、右に1、上に\(\frac{3}{4}\)だけれど、目盛りがないから点が打てないね。
右に1、上に\(\frac{3}{4}\)(打てない)
右に2だったら、上に\(\frac{3}{4}\)×2=\(\frac{3}{2}\)(打てない)
右に3だったら、上に\(\frac{3}{4}\)×3=\(\frac{9}{4}\)(打てない)
右に4だったら、上に\(\frac{3}{4}\)×4=3(これなら打てる!)
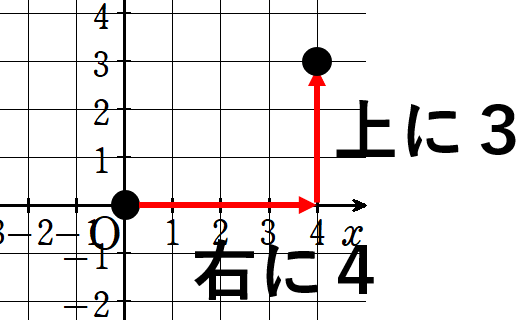
y=-\(\frac{3}{4}\)xのグラフを書こう
右に1、上に-\(\frac{3}{4}\)(打てない)
右に2だったら、上に-\(\frac{3}{4}\)×2=-\(\frac{3}{2}\)(打てない)
右に3だったら、上に-\(\frac{3}{4}\)×3=-\(\frac{9}{4}\)(打てない)
右に4だったら、上に-\(\frac{3}{4}\)×4=-3(これなら打てる!)
原点から右に4、上に-3行ったところに点を打っていけばいいね。上に-3ということは、下に3行くってことだね。
やっぱり、比例定数が分数の時は、「右に分母の数行って、上に分子の数行けばいい」んだね。
【裏ワザ】比例定数が分数のとき、グラフを速く書く方法まとめ
- 比例定数の分母の数の分だけ、「右」に行って点を打つ。
- 比例定数の分子の数の分だけ、「上」に行って点を打つ。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。





分かりやすかった