角柱と円柱・角錐と円錐の体積の求め方と公式を解説「立体の体積」
角柱と円柱・角錐と円錐の体積の求め方と公式を解説「立体の体積」のPDF （12枚） がダウンロードできます。
PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。
PDF教材をよく使う方は、有料プランで広告なし・透かしなしPDFを使い放題で利用できます。
中学数学で学習する「立体の体積」について、角柱と円柱の体積の求め方と公式、角錐と円錐の体積の求め方と公式をわかりやすく説明するよ。
テスト対策に覚えるべきポイントを確認しよう！
角柱の体積の求め方
角柱って、三角柱や四角柱や五角柱などをひとまとめにしたものだったよね。
角柱の体積は次の式で求められるよ。
底面積×高さ
小学校でもやったことがあると思うけど、実際に問題をやってみよう。
次の三角柱の体積を求めなさい。
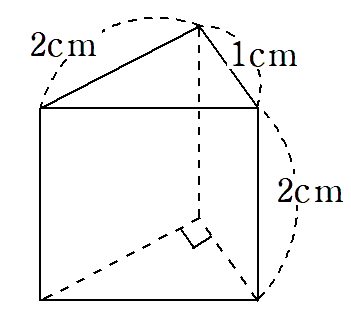
STEP１ 底面積を求めよう。
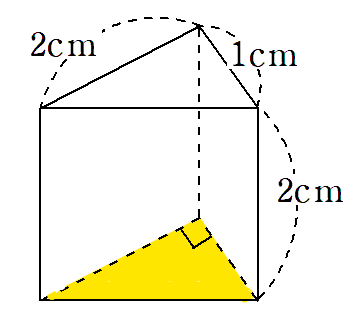
底面積っていうのは、底面の面積のことだったよね。上の三角柱の底面は、底辺が１cm、高さが２cmの三角形だから、底面積は
（底辺）×（高さ）÷２ ←三角形の面積を求める公式
＝１×２÷２
＝１cm2
STEP2 体積を求めよう。
底面積が１cm2とわかったから、体積は
（底面積）×（高さ） ←角柱の体積を求める公式
＝１×２
＝２cm3
と求めることができるね。
円柱の体積の求め方
円柱の体積も角柱と同じように求めることができるよ。
底面積×高さ
実際に問題を見てみよう。
次の円柱の体積を求めなさい。
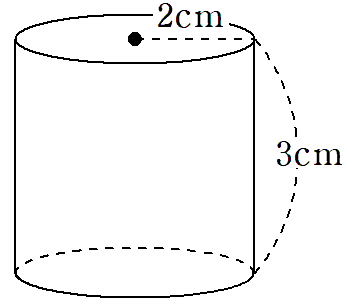
STEP１ 底面積を求めよう。
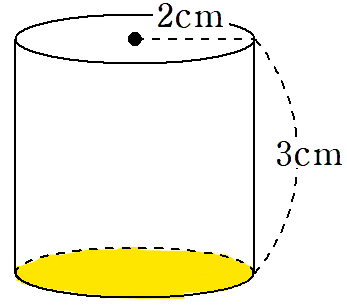
底面は、半径２cmの円だから、底面積は
（半径）×（半径）×（円周率） ←円の面積を求める公式
＝２×２×π
＝４π cm2
小学校では「円周率」を3.14で計算したと思うけど、中学生では「π（パイ）」を使うよ。
STEP2 体積を求めよう。
底面積が４πcm2とわかったから、体積は
（底面積）×（高さ） ←円柱の体積を求める公式
＝４π×３
＝１２π cm3
と求めることができるね。よく「π（パイ）」をつけ忘れることが多いから気をつけよう。
角柱・円柱の体積の公式
角柱も円柱も同じ体積の公式が使えるよ、「○○柱はこういう公式だ」と覚えてしまってもいいかもね。
角柱・円柱の体積の公式
（底面積）×（高さ）
底面の形によって、（底面積）の求め方が変わってくるよ。例えば次の通りだよ。
面積を求める公式
長方形の面積：たて×よこ
三角形の面積：底辺×高さ÷２
円の面積：半径×半径×π
台形の面積：（上底＋下底）×高さ÷２
角錐の体積の求め方
角錐って、三角錐や四角錐や五角錐などをひとまとめにしたものだったよね。
角錐の体積は次の式で求められるよ。
底面積×高さ×\(\frac{１}{３}\)
なんで\(\frac{１}{３}\)倍するのかは後で説明するね。
実際に問題をやってみよう。
次の正四角錐の体積を求めなさい。
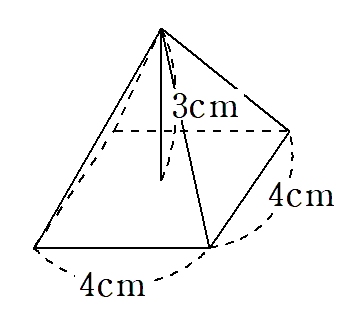
STEP１ 底面積を求めよう。
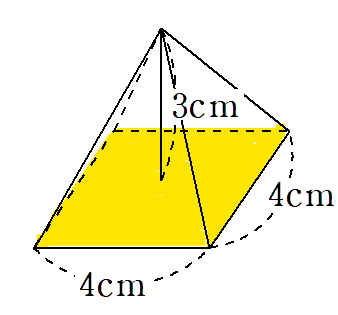
底面は、１辺が４ｃｍの正方形だから、底面積は
（１辺）×（１辺） ←正方形の面積を求める公式
＝４×４
＝１６ cm2
STEP2 体積を求めよう。
底面積が１６cm2とわかったから、体積は
（底面積）×（高さ）×\(\frac{１}{３}\) ←角錐の体積を求める公式
＝１６×３×\(\frac{１}{３}\)
＝１６ cm3
と求めることができるね。
円錐の体積の求め方
円錐の体積も次のような式で求めることができるよ。
底面積×高さ×\(\frac{１}{３}\)
実際に問題をやってみよう。
次の円錐の体積を求めなさい。
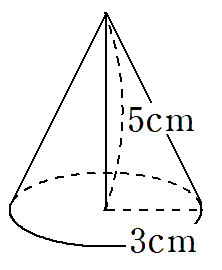
STEP１ 底面積を求めよう。
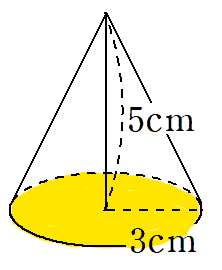
底面は、半径３cmの円だから、底面積は
（半径）×（半径）×（円周率） ←円の面積を求める公式
＝３×３×π
＝９π cm2
STEP2 体積を求めよう。
底面積が９πcm2とわかったから、体積は
（底面積）×（高さ）×\(\frac{１}{３}\)
＝９π×５×\(\frac{１}{３}\)
＝１５πcm3
と求めることができるね。
角錐・円錐の体積の公式
角錐も円錐も同じ体積の公式が使えるよ、「○○錐はこういう公式だ」と覚えてしまってもいいかもね。
とにかく「○○錐」は\(\frac{１}{３}\)がポイントだよ。
角錐・円錐の体積の公式
（底面積）×（高さ）×\(\frac{１}{３}\)
錐の体積が柱の\(\frac{１}{３}\)倍になっている
○○錐の体積は○○柱の\(\frac{１}{３}\)倍になるんだよ。
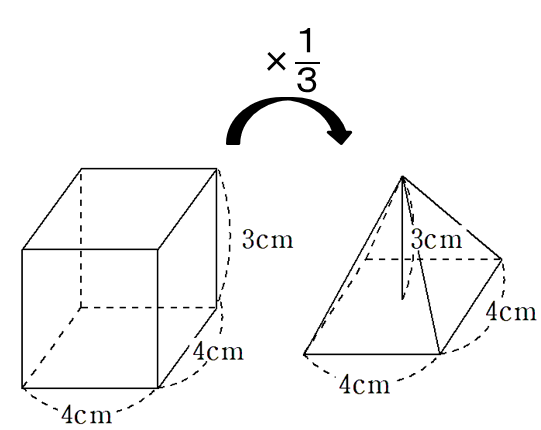
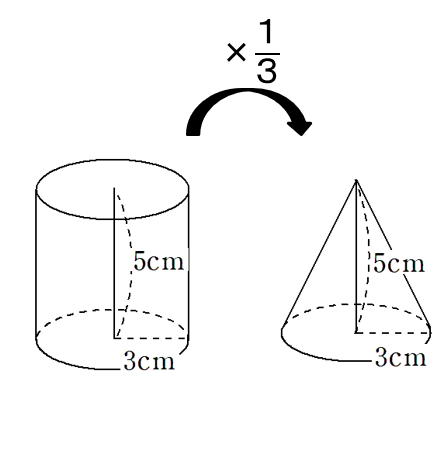
錐の体積が柱の\(\frac{１}{３}\)倍になる理由
○○錐の体積は○○柱の\(\frac{１}{３}\)倍になる理由を紹介するね。ここでは、四角錐が四角柱の\(\frac{１}{３}\)倍になることを取り上げるよ。
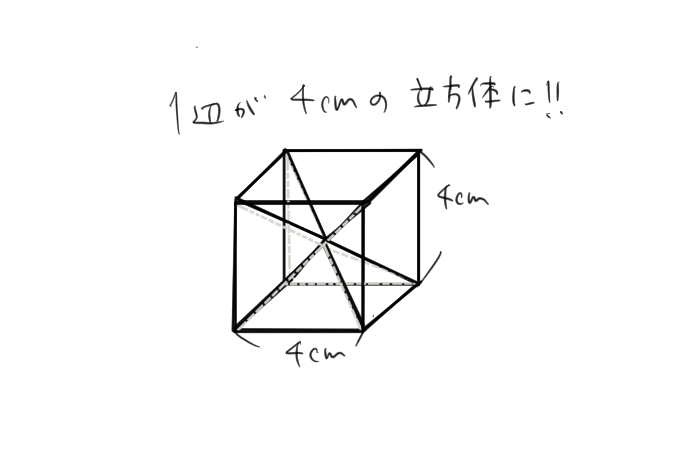
次のような正四角錐を考えよう。
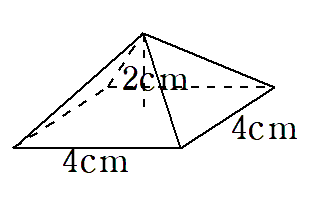
この正四角錐を６つ組み合わせると下のような１辺が４ｃｍの立方体になるよね。
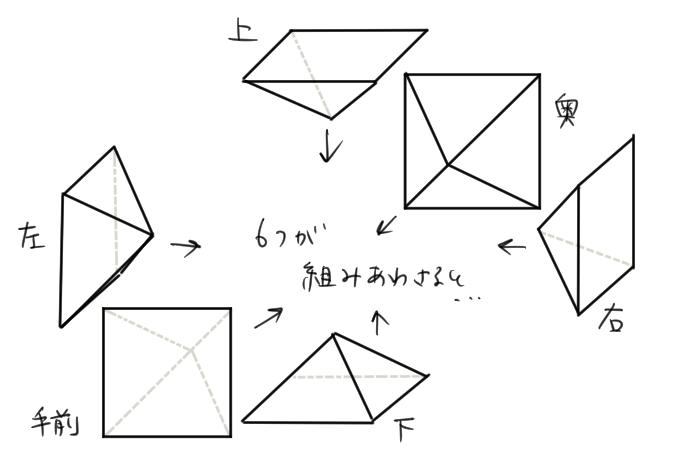
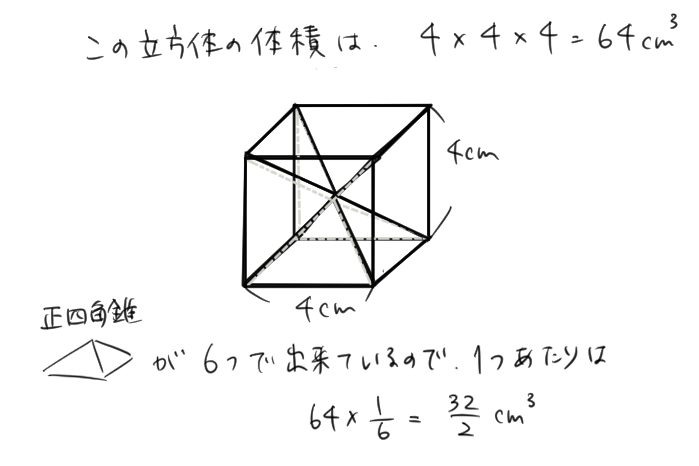
この立方体の体積は
（１辺）×（１辺）×（１辺）
＝４×４×４
＝６４cm
だね。
じゃあ、正四角錐１つ分の体積は立方体の\(\frac{１}{６}\)になるから
６４×\(\frac{１}{６}\)
＝\(\frac{３２}{３}\) cm3
と求まるね。
正四角錐の体積が\(\frac{３２}{３}\) cm3ということがわかったよ。
もし、
下の正四角錐の体積が
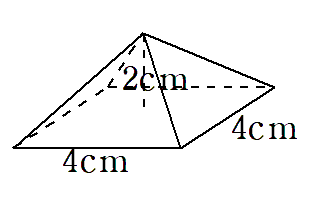
（底面積）×（高さ）だったとすると
＝４×４×２
＝３２cm3
になっちゃうね。ただ、実際の体積は\(\frac{３２}{３}\) cm3なので
（底面積）×（高さ）×\(\frac{１}{３}\)
になるってことだよ。
柱の体積の\(\frac{１}{３}\)が錐の体積になることがわかったかな。
この教材をもっと活用したい方へ
PDFを印刷して復習したい方は、無料ダウンロードページから教材を確認できます。
先生としてドリルを配布したい方は、無料会員登録でクラス配布・自動採点機能を使えます。
運営者情報
yumineko
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。
-
-
もっちゃんさん
ポイントは、底面全体で高さの変化が均一かどうかです。
平行四辺形の場合、向かい合う辺が平行で形がそろっているため、底面上で高さが比較的均一に変化しやすく、
「底面積 × 平均高さ」
で体積を求めやすくなります。一方、台形の場合は、底面の形が左右で均一ではないため、場所によって高さの分布の重みが変わります。
そのため、単純に4頂点の高さの平均を使うだけでは、底面全体の体積を正確に表せないことがあります。なので、三角形に分けてそれぞれの断頭三角柱として計算すると、より正確に求めやすくなります。
つまり、
・平行四辺形 → 高さ分布が均一なので平均高さが使いやすい
・台形 → 高さ分布に偏りがあるため、そのままでは使いにくいという違いです。
少し発展的な内容ですが、「高さの平均にも形によって使いやすさが変わる」と考えると整理しやすいですね。
-
ご回答いただきありがとうございます。どうもこういう数学は苦手で高校以降だんだん話が抽象的になっていくのかと思うと憂鬱です。
高さの分布の重みが変わるとはこういう事ですか？
柱体下側の台形の底面を構成する点の集合と斜めに切断されて出来る台形上の対応する点を結びそれを個々の高さとしたときに仮にｘ軸方向に左から右に移動させていったとき、この高さの集まり方が左から右に向かっときに均一に変化せずに位置によって変わるというニュアンスなんですか？
平行四辺形と台形との違いがイメージしにくいです。-
そもそも、断頭四角柱の体積を求めるときに、平均の高さを出して求めるというのは、どういうことかというと
イメージとしては、「でこぼこに盛られた砂をならして、全体を同じ高さにする」感じですよね。詳しくいうと、
高いところの分を、低いところへならす
↓
全体が同じ高さになったと考える
↓
底面積 × ならした高さで体積を出すということです。
ただし、ここで大事なのは、
どんな形でも単純に角の高さを平均すればいいわけではない、ということです。平行四辺形のように、形の広がり方がバランスよい場合は、角の高さの平均が全体の平均として使いやすいです。
でも台形のように、広い部分と狭い部分がある形では、
高いところが広いのか、低いところが広いのか
によって、全体の平均高さが変わります。たとえば、
高い部分が広い → 高さは高めになる
低い部分が広い → 平均高さは低めになるので、ただ4つの角の高さを足して4で割るだけでは、正確な「全体の平均高さ」にならないことがあるんです。
そのため、もっちゃんさんが最初に書いていただいた通り、「平行四辺形ならそのまま平均高さが使えるけれど、台形では三角形に分けて、それぞれで平均高さを出す必要がある」ということになります。
台形では「ならした高さ」を出すのが単純ではない、ということになるのですが、この考え方ならどうでしょうか？
-
ありがとうございます。切断された台形の各頂点の単純平均がならしたときの高さと平均高さは一致しないから使えないという理屈はわかります。単純に考えるのであれば平行四辺形の対角線の交点は対角線の中点で交わるので平均高さは一致するが、台形はそうならないので高さの平均は一致しないというふうに考えてもよいんですかね？
-
はい、その考え方はイメージとしてかなりわかりやすいと思います！
平行四辺形は、対角線が互いの中点で交わるように、図形全体の形がバランスよく整っているため、高さの平均も比較的一致しやすいです。
一方、台形はそのような対称性が弱く、広い部分と狭い部分があるため、単純に頂点の高さを平均しただけでは、底面全体をならしたときの平均高さとズレやすくなります。
つまり、
・平行四辺形 → バランスがよく平均しやすい・台形 → 広さに偏りがあり単純平均しにくい
という理解で大丈夫です。
-
ありがとうございます。切断された台形の各頂点の単純平均がならしたときの高さと平均高さは一致しないから使えないという理屈はわかります。単純に考えるのであれば平行四辺形の対角線の交点は対角線の中点で交わるので平均高さは一致するが、台形はそうならないので高さの平均は一致しないというふうに考えてもよいんですか？
-
-
-
-
また教えてください。断頭四角柱の体積を求めるとき底面積ｘ平均高さを利用する場合についてです。この場合、底面の四角形は平行四辺形の仲間に限られ、台形の場合はそのまま平均の高さを使うことができず三角形に二分してそれぞれの断頭三角柱の平均高さからの体積の和を計算することになります。なぜ底面が台形であれば、なぜそのまま平均高さが使えないのかすっきりした答えが見つかりません。 よろしくお願いいたします。