「反比例のグラフ」の書き方をわかりやすく解説(双曲線とは)
中学1年生の数学で学習する「反比例」について、反比例の関係を表す表と、式からグラフを書く方法をわかりやすく解説しているよ。
表から反比例のグラフを書いてみよう
表から反比例のグラフを書くときに一番大切なことは座標を理解できているかだから、わからなかったらグラフの座標について説明しているページにもどって復習をしよう。
比例でも座標が大事だったけど、反比例でも大事なんだよ。
次の表はxとyが反比例の関係であることを表しているよ。
だってxが2倍、3倍になると、yは\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍になっているからね。

では、この表から反比例のグラフを書いてみよう。
表からグラフを書くときは、表を「縦のかたまり」で見ていくよ。
たとえば、「xが1のとき、yは4」になっているね。

ということは、この反比例をグラフにすると、xが1のとき、yは4の場所に点がくるということなんだ。
座標(住所)で表すと、(1,4)になるね。
こうやって、表にあるxとyの数字を、縦のかたまりごとに全部座標で表してみるよ。
x=1のとき、y=4
→座標で表したら(1,4)
x=2のとき、y=2
→座標で表したら(2,2)
x=3のとき、y=\(\frac{4}{3}\)
→座標で表したら(3,\(\frac{4}{3}\))
x=4のとき、y=1
→座標で表したら(4,1)
x=-1のとき、y=-4
→座標で表したら(-1,-4)
x=-2のとき、y=-2
→座標で表したら(-2,-2)
x=-3のとき、y=-\(\frac{4}{3}\)
→座標で表したら(-3,-\(\frac{4}{3}\))
x=-4のとき、y=-1
→座標で表したら(-4,-1)
このことからグラフは次の点を通ることがわかるね。
(1,4)(2,2)(3,\(\frac{4}{3}\))(4,1)(-1,-4)(-2,-2)(-3,-\(\frac{4}{3}\))(-4,-8)
これらの点をグラフ上にとってみると次のようになるよ。ちなみに(3,\(\frac{4}{3}\))はおよその場所に点をとったよ。
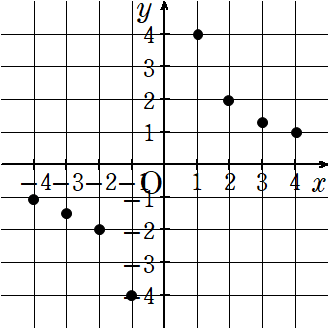
点をとったら線を結べばいいんだけど、どうやって結ぶかというと、反比例のグラフは曲がった線(曲線)になるよ。だから定規を使って書くのはダメなんだ!
反比例のグラフの特徴は、2つの「曲線」になるんだ。2つの曲線は原点に対して点対称になっているね。そして比例とは違って、「原点」は通らないんだよ。
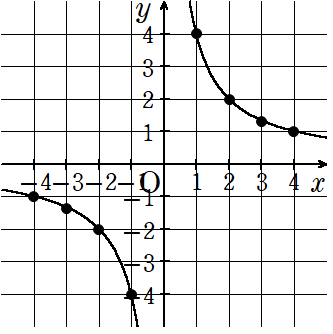
よくある間違いはこんな感じで、y軸の右側の点と左側の点を結んでしまうこと。反比例のグラフはx軸やy軸をまたがないと覚えておこう。
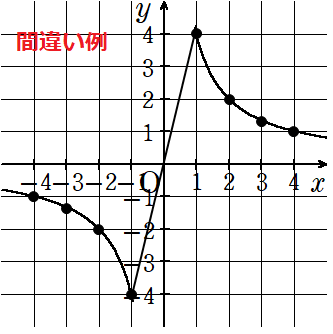
表から反比例のグラフを書く手順
- 表を縦にみて、xとyの値を読み取る。
例:x=1のときy=4 - 読み取ったxとyの値をもとに座標に点を書きこむ。
例:(1,4)に点を書きこむ - 書きこんだ点を曲線で結ぶ。
※y軸の右側の点、左側の点でそれぞれ結ぶ
反比例の表で0の下が×(ばつ)の理由
反比例のグラフがx軸やy軸をまたがないことにも関係しているんだけど、反比例の表では、x=0のときのyの値は計算ができないから「×(ばつ)」になっているよ。
反比例ってy=\(\frac{a}{x}\)っていう形だったよね。x=0だったら、y=\(\frac{a}{0}\)=a÷0になって計算ができないよ。だから「×」を書くんだ!
a÷0が計算できない理由
a÷0って計算できないから「×(ばつ)」を書くんだったよね。実は割り算には「0(ゼロ)」で割ってはいけないというルールがあるんだ。なんで割ってはいけないかを説明するね。
① 8÷4=2
② 8÷8=1
③ 8÷0=?
この計算ってこういう見方もできるよね。
① 8っていうのは、4×2
② 8っていうのは、8×1
つまり
○÷★=△という式があったとき、★と△をかけたら○になるってことだよね。同じように考えると③は
③ 8っていうのは、?×0
「?」がいくつか考えればいいんだけど、「?」がいくつであっても「0(ぜろ)」をかけたら0になってしまう。(8にならない)
だから、8÷0という計算はできないから、0で割っていけないんだよ。
式から反比例のグラフを書いてみよう
それでは、今度は「反比例の式」から反比例のグラフを書く方法を説明するよ。
比例みたいに比例定数に注目して、xが1増えたら、yは○○増えるみたいな必殺技はないんだ。
だから、反比例のグラフは比例とは違って地道に座標を取っていくんだよ。
実際に例題を見てみよう。
y=\(\frac{6}{x}\)のグラフ
式から反比例のグラフを書くために、xに数字を代入していくよ。ただ、適当な数字を入れるのではなく、\(\frac{6}{x}\)が整数になるようなxを代入しよう。
●まずは正の数を考えよう。
x=1のとき y=\(\frac{6}{x}\)=\(\frac{6}{1}\)=6
x=2のとき y=\(\frac{6}{x}\)=\(\frac{6}{2}\)=3
x=3のとき y=\(\frac{6}{x}\)=\(\frac{6}{3}\)=2
x=4とx=5を代入してもいいけど、答えは分数になって、座標をとれないよね。
x=6のとき y=\(\frac{6}{x}\)=\(\frac{6}{6}\)=1
x=7以上の数を代入しても\(\frac{6}{x}\)は分数になっちゃうからやらないよ。
●次に負の数を考えよう。
x=-1のとき y=\(\frac{6}{x}\)=\(\frac{6}{-1}\)=-6
x=-2のとき y=\(\frac{6}{x}\)=\(\frac{6}{-2}\)=-3
x=-3のとき y=\(\frac{6}{x}\)=\(\frac{6}{-3}\)=-2
x=-4とx=-5を代入してもいいけど、答えは分数になって、座標をとれないよね。
x=-6のとき y=\(\frac{6}{x}\)=\(\frac{6}{-6}\)=-1
x=-7以下の数を代入しても\(\frac{6}{x}\)は分数になっちゃうからやらないよ。
この計算から、(1,6)(2,3)(3、2)(6,1)(-1,-6)(-2,-3)(-3、-2)(-6,-1)を通ることがわかるよね。
だからy=\(\frac{6}{x}\)のグラフは下のようになるよ。
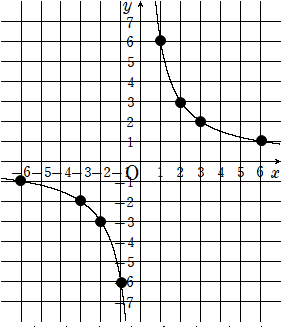
y=-\(\frac{4}{x}\)のグラフ
式から反比例のグラフを書くために、xに数字を代入していくよ。ただ、適当な数字を入れるのではなく、-\(\frac{4}{x}\)が整数になるようなxを代入しよう。
●まずは正の数を考えよう。
x=1のとき y=-\(\frac{4}{x}\)=-\(\frac{4}{1}\)=-4
x=2のとき y=-\(\frac{4}{x}\)=-\(\frac{4}{2}\)=-2
x=3を代入してもいいけど、答えは分数になって、座標をとれないよね。
x=4のとき y=-\(\frac{4}{x}\)=-\(\frac{4}{4}\)=-1
x=5以上の数を代入しても-\(\frac{4}{x}\)は分数になっちゃうからやらないよ。
●次に負の数を考えよう。
x=-1のとき y=-\(\frac{4}{x}\)=-\(\frac{4}{-1}\)=4
x=-2のとき y=-\(\frac{4}{x}\)=-\(\frac{4}{-2}\)=2
x=-3を代入してもいいけど、答えは分数になって、座標をとれないよね。
x=-4のとき y=-\(\frac{4}{x}\)=-\(\frac{4}{-4}\)=1
x=-5以下の数を代入しても-\(\frac{4}{x}\)は分数になっちゃうからやらないよ。
この計算から、(1,-4)(2,-2)(4、-1)(-1,4)(-2,2)(-4、1)を通ることがわかるよね。
だからy=-\(\frac{4}{x}\)のグラフは下のようになるよ。今までのグラフは右上と左下にできていたけど、y=-\(\frac{4}{x}\)は右下と左上にあるね。
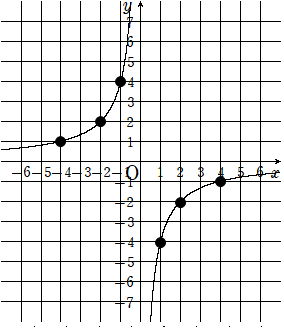
反比例のグラフでよくある間違いはこんな感じ。
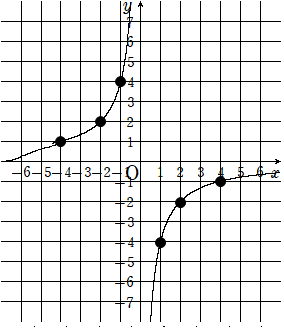
左上にあるグラフがx軸に交わっていることがわかるかな?反比例のグラフは絶対にx軸やy軸に交わらないんだよ。
グラフの端っこまで集中してね。
x軸、y軸に交わらない理由
反比例のグラフがx軸、y軸に交わらない理由だけど、ちゃんと習うのは、高校3年生の「極限」という単元になるんだ。
ただ、ここではx軸に交わらない理由についてざっくりと説明するね。
x軸に交わるってことはy=0になることだよね。y=-\(\frac{4}{x}\)はxがどんなに小さくなってもyは0にならないよ。
代入して確かめてみよう
x=-1000のときy=-\(\frac{4}{-1000}\)=0.004
x=-10000のときy=-\(\frac{4}{-10000}\)=0.0004
x=-100000のときy=-\(\frac{4}{-100000}\)=0.00004
xの値がどんなに小さくなってもyは0にならないから、反比例のグラフはx軸に交わらないことがわかるね。
双曲線とは
さっきまで書いていた反比例のグラフは「双曲線」と呼ばれているよ。「双」は「双子」という言葉があるように、「2つ」という意味。「曲線」は曲がった線。だから「双曲線」とは、2つの曲がった線のことだね。
反比例のグラフは必ず2つ曲線ができるんだ。
y=\(\frac{a}{x}\)の比例定数aによって、どこにグラフができるかが決まるよ。
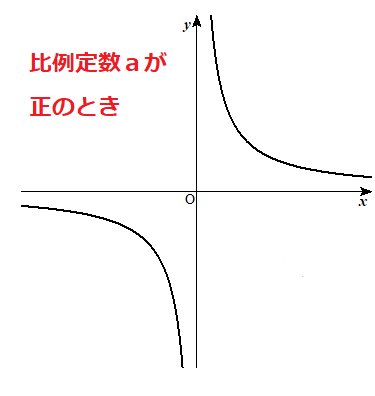
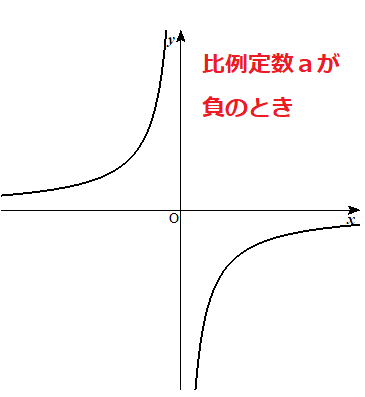
反比例のグラフの特徴
反比例のグラフの特徴をまとめると次の通り。
反比例のグラフの特徴
- 双曲線(2つの曲がった線)になる。
- 原点に対して点対称。
- 原点やx軸やy軸は通らない。
- y=\(\frac{a}{x}\)の比例定数aによって、どこにグラフができるかが決まる。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



分からないところが無くなりました!