「一次方程式の利用」道のり・時間・割合などの問題の解き方を解説
中学1年生の数学で学習する「一次方程式」を使って、道のりや時間、割合についての問題を解く方法をわかりやすく解説するよ。
文章題のどこをヒントにして、文字にすればいいのか、式を作ればいいのか、ひとつひとつくわしく説明するよ。
一次方程式の利用「個数の問題」
一次方程式を利用して「個数の問題」を解いてみよう。一次方程式の利用の中でも簡単な問題だと思うから、がんばろう!
問
1個240円のケーキ4個と1個90円のプリンを何個か買ったところ、代金の合計が1500円になりました。プリンを何個買ったでしょうか。
ステップ1:図でイメージする。
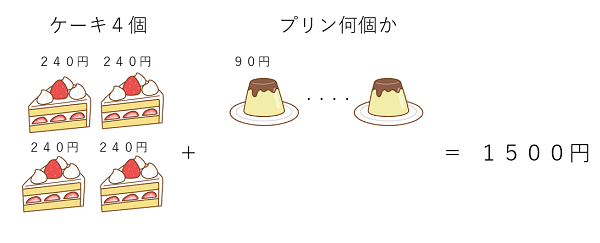
感のいい人はプリン何個買ったかわかるんじゃない?
ステップ2:求めたいものを確認する。
問題をもう一度見てみよう。
問
1個240円のケーキ4個と1個90円のプリンを何個か買ったところ、代金の合計が1500円になりました。プリンを何個買ったでしょうか。
赤字のところが今回求めたいものだよね。一次方程式では、求めたいものを「x」と置くので、今回は
プリンをx個買った
としよう。
ステップ3:表にまとめる
今回求めたいのはプリンの個数だよね。だからプリンをx個買ったとして、表にまとめてみたよ。(今回の問題で必要ないところは「・・・・」にしたよ)
| ケーキ | プリン | 合計 | |
| 1個の値段 | 240 | 90 | ・・・・ |
| 買った個数 | 4 | x | ・・・・ |
| 代金 | ① | ② | 1500 |
表の①②をうめよう。
①1個240円のケーキ4個だから、ケーキだけで240×4=960円だね。
②1個90円のケーキx個だから、プリンだけで90×=90x円だね。
もう一度表を確認するとこんな感じになるよ。
| ケーキ | プリン | 合計 | |
| 1個の値段 | 240 | 90 | ・・・・ |
| 個数 | 4 | x | ・・・・ |
| 代金 | 960 | 90x | 1500 |
ステップ3:方程式をたてよう。
表の一番下に注目しよう。
| ケーキ | プリン | 合計 | |
| 代金 | 960 | 90x | 1500 |
(ケーキの代金)+(プリンの代金)=1500円になるから、
960 +90x =1500
という方程式がたつよね。
ステップ4:方程式を解こう。
960 +90x =1500
+90x =1500-960
+90x =540
x =6
プリンの個数をx個としたから、プリンを6個買ったということがわかるね。
一次方程式の利用「値段の問題」
一次方程式を利用して「値段の問題」を解いてみよう。「個数の問題」ができたら100%、この問題もできると思うよ。
問
1個240円のケーキ4個とプリン6個を買ったところ、代金の合計が1500円になりました。プリン1個の値段を求めなさい。
ステップ1:図でイメージする。
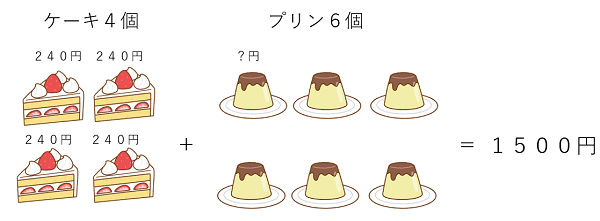
感のいい人はプリンの値段がわかるんじゃない?
ステップ2:求めたいものを確認する。
問題をもう一度見てみよう。
問
1個240円のケーキ4個とプリン6個を買ったところ、代金の合計が1500円になりました。プリン1個の値段を求めなさい。
赤字のところが今回求めたいものだよね。一次方程式では、求めたいものを「x」と置くので、今回は
プリンを1個の値段をx円
とします。
ステップ3:表にまとめる
今回求めたいのはプリンの値段だよね。だからプリン1個x円だとして、表にまとめてみたよ。(今回の問題で必要ないところは「・・・・」にしたよ)
| ケーキ | プリン | 合計 | |
| 1個の値段 | 240 | x | ・・・・ |
| 買った個数 | 4 | 6 | ・・・・ |
| 代金 | ① | ② | 1500 |
①②に入るものを考えよう。
①1個240円のケーキ4個だから、ケーキだけで240×4=960円だね。
②1個x円のケーキ6個だから、プリンだけで6×=6x円だね。
もう一度表を確認するとこんな感じになるよ。
| ケーキ | プリン | 合計 | |
| 1個の値段 | 240 | x | ・・・・ |
| 個数 | 4 | 6 | ・・・・ |
| 代金 | 960 | 6x | 1500 |
ステップ4:方程式をたてよう。
表の一番下に注目しよう。
| ケーキ | プリン | 合計 | |
| 代金 | 960 | 6x | 1500 |
(ケーキの代金)+(プリンの代金)=1500円になるから、
960 +6x =1500
という方程式がたつよね。
ステップ5:方程式を解こう。
方程式をたてられたら、後は楽勝だね!
960 +6x =1500
+6x =1500-960
+6x =540
x =90
プリン1個x円としたから、プリン1個90円だということがわかるね。
一次方程式の利用「道のりの問題」
一次方程式を利用して「道のりの問題」を考えてみよう。中学校の「道のりの問題」を解く前に小学校の復習をしよう。
小学校の復習
小学校で、速さ、時間、道のりを学習したよね?こんなやつ覚えなかった?
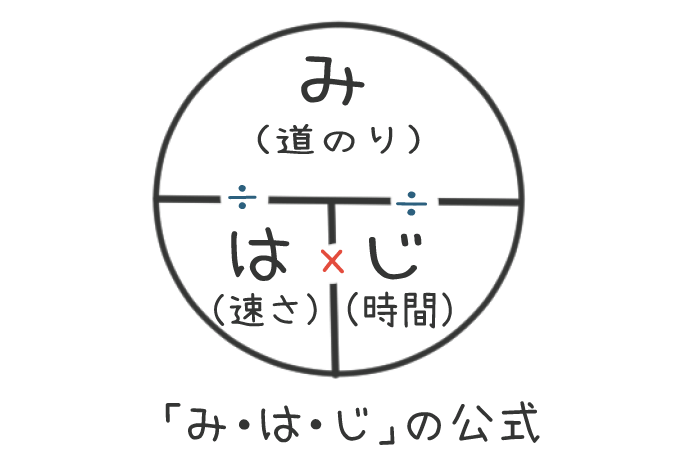
この図からわかることは、次の通りだよ。
①み(道のり)=は(速さ)×じ(時間)
②は(速さ)=み(道のり)÷じ(時間)
③じ(時間)=み(道のり)÷は(速さ)←「道のりの問題」ではこの関係を使うよ!
一次方程式を利用して「道のりの問題」を解く
「道のりの問題」は次の通りだよ。
問
家から1500mのところにある学校に向かいました。分速50mで歩いていましたが、途中から分速100mで走りました。合計で20分で着きました。歩いた道のりは何mだったしょうか。
ステップ1:図でイメージする。
どういう状況かを図で確認しよう。
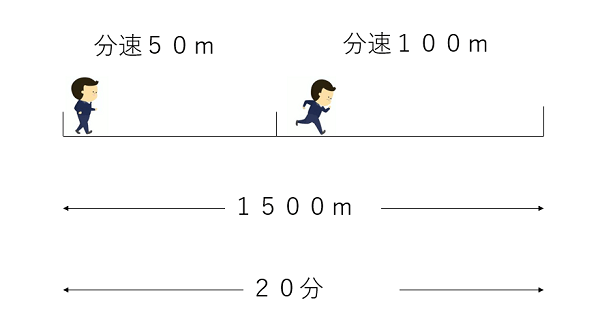
のんびり歩いていて、途中で何かに気づいて猛ダッシュしたことって経験ないかな?
ステップ2:求めたいものを確認する。
問題をもう一度見てみよう。
(問)
家から1500mのところにある学校に向かいました。分速50mで歩いていましたが、途中から分速100mで走りました。合計で20分で着きました。歩いた道のりは何mだったしょうか。
赤字のところが今回求めたいものだよね。一次方程式では、求めたいものを「x」と置くので、今回は
歩いた道のりをxm
とします。
ステップ3:表にまとめる
速さ、時間、道のりを表にまとめよう。今回は「歩き」と「走り」と「合計の時間や距離」もあるから次のような表になるよ。(今回の問題で必要ないところは「・・・・」にしたよ)
| 歩き | 走り | 合計 | |
| 速さ(m/分) | 50 | 100 | ・・・・ |
| 時間(分) | ③ | ④ | 20 |
| 道のり(m) | ① | ② | 1500 |
①②に入るものを考えよう。
①歩いた道のりをxmとしたので、①には「x」が入るよ。
②走った道のりを考えよう。
歩いた道のりと走った道のりを足したら1500mになるということは、
(歩いた道のり)+(走った道のり)=1500
x +(走った道のり)=1500
だから、
(走った道のり)は1500-x(m)になるよね。
今の段階で表は次のようになっているよ。残るは③と④だね。
| 歩き | 走り | 合計 | |
| 速さ(m/分) | 50 | 100 | ・・・・ |
| 時間(分) | ③ | ④ | 20 |
| 道のり(m) | x | 1500-x | 1500 |
③④に入るものを考えよう。
速さ、時間、道のりの関係を使おう。
時間=道のり÷速さなので
③歩いた時間=x÷50=\(\frac{x}{50}\)
④走った時間=(1500-x)÷100=\(\frac{1500-x}{100}\)
表をもう一度確認しよう。
| 歩き | 走り | 合計 | |
| 速さ(m/分) | 50 | 100 | ・・・・ |
| 時間(分) | \(\frac{x}{50}\) | \(\frac{1500-x}{100}\) | 20 |
| 道のり(m) | x | 1500-x | 1500 |
ステップ4:方程式をたてる
次のことはわかるかな?
方程式をたてるポイント
・(歩きの時間)+(走りの時間)=(全部の時間)
\(\frac{x}{50}\)+\(\frac{1500-x}{100}\)=20
という方程式がたつよ。
ステップ5:方程式を解く。
最後に分数をふくむ方程式を解いてみよう。
\(\frac{x}{50}\)+\(\frac{1500-x}{100}\)=20
分数の方程式は分母を払う必要があるんだったよね。払うために両辺に「50」と「100」の最小公倍数「100」をかけよう。
\(\frac{x}{50}\)×100+\(\frac{1500-x}{100}\)×100=20×100
2x+1500-x=2000
x =2000-1500
x =500
解はx=500だね。歩いた道のりが「x」だったから、500m歩いたということがわかるね。
一次方程式の利用「時間の問題」
一次方程式を利用して「時間の問題」を考えてみよう。
中学1年生でよく出てくる「時間の問題」は、「1人がもう1人に追いつくまでの時間を求める問題」が多いよ。
(問)
弟は家を出発して学校に向かいました。その4分後に、兄は家を出発して弟を追いかけました。弟は分速50m、兄は分速70mで歩くとすると、兄は家を出発してから何分後に追いつきますか?
ステップ1:図でイメージする。
どういう状況かを図で確認しよう。
0分のとき 弟も兄も家にいるよね。
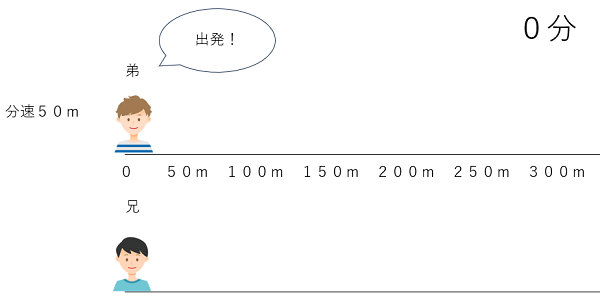
1分のとき 弟は50m進んでいるよ。
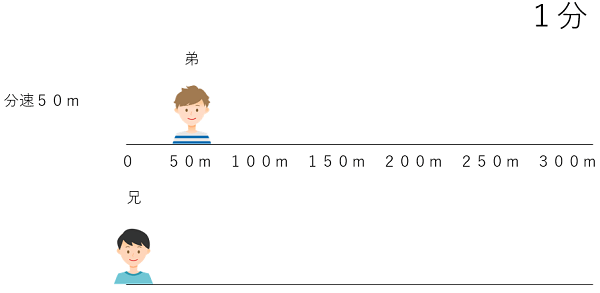
4分のとき 弟は200m進んでいるよ。兄が出発するよ。
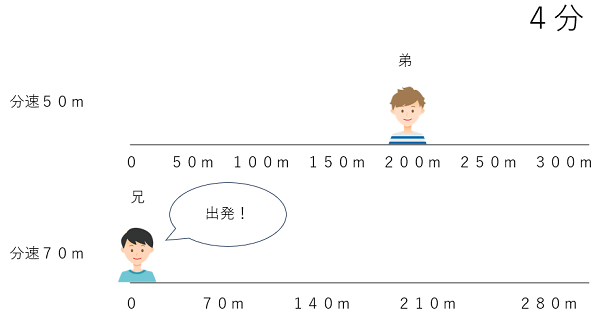
5分のとき 弟は250m進んでいるよ。兄は70m進んでいるよ。
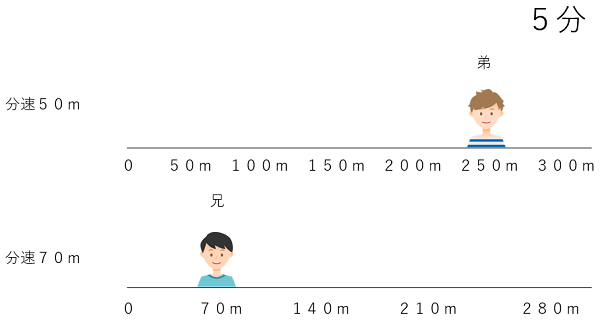
兄の方が速いので、いつか追いつくよね。この問題は何分後に追いつくかを求めたいんだったね。
この図の続きを書いていったら、何分後に追いつくかわかりそうだね。
確かに求めることができるけど、一次方程式を利用したやり方をできるようにしよう。
ステップ2:求めたいものを確認する。
問題をもう一度見てみよう。
(問)
弟は家を出発して学校に向かいました。その4分後に、兄は家を出発して弟を追いかけました。弟は分速50m、兄は分速70mで歩くとすると、兄は家を出発してから何分後に追いつきますか?
赤字のところが今回求めたいものだよね。一次方程式では、求めたいものを「x」と置くので、今回は
兄は家を出発してからx分後に追いつく
とします。
図にすると下のようになるよ。兄が出発してから追いつくまでの時間がxになるよ。
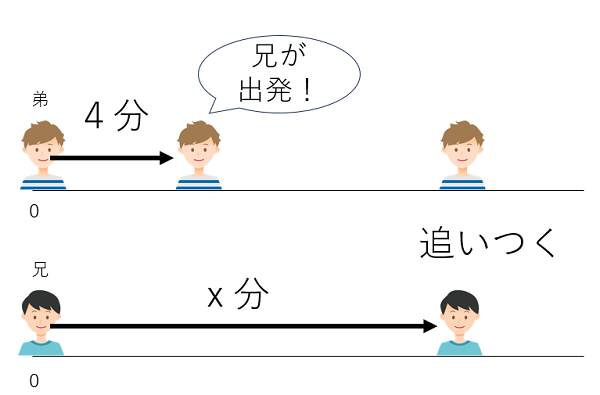
ステップ3:表にまとめる
速さ、時間、道のりを表にまとめよう。今回の登場人物は2人なので次のような表になるよ。また、2人の速さは始めからわかっているね。
| 弟 | 兄 | |
| 速さ(m/分) | 50 | 70 |
| 時間(分) | ② | ① |
| 道のり(m) | ③ | ④ |
①②に入るものを考えよう。
①兄が追い付くまでに歩いた時間をx分としたので、①には「x」が入るよ。
②弟が追い付かれるまでに歩いた時間はどうなるかな?
下の図で赤矢印にかかった時間は同じだよね。
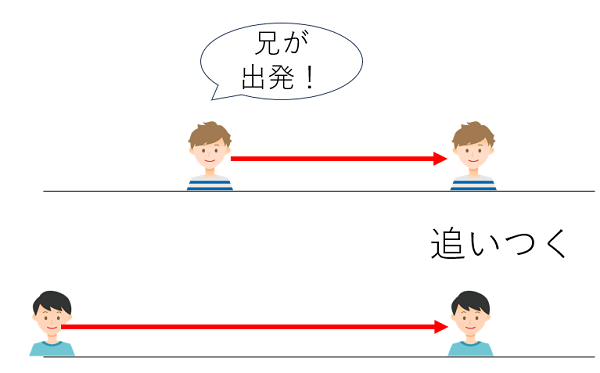
だから下のようになるよ。
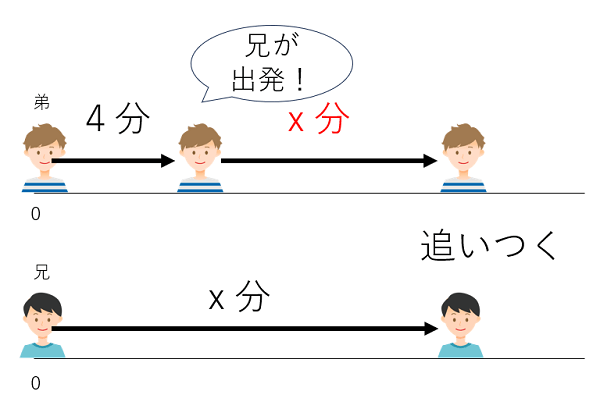
弟からしてみたら、追いつかれるまでに歩いた時間は4+x(分)になるので、②には「4+x」が入る。
今の段階で表は次のようになっているよ。残るは③と④だね。
| 弟 | 兄 | |
| 速さ(m/分) | 50 | 70 |
| 時間(分) | 4+x | x |
| 道のり(m) | ③ | ④ |
③④に入るものを考えよう。
③④を求めるには、速さ、時間、道のりの関係を使おう。
道のり=速さ×時間で求まるから、次のようになるよ。
③弟の歩いた道のり=50×(4+x)=50(x+4)
④兄の歩いた道のり=70×x=70x
表をもう一度確認しよう。
| 弟 | 兄 | |
| 速さ(m/分) | 50 | 70 |
| 時間(分) | 4+x | x |
| 道のり(m) | 50(4+x) | 70x |
ステップ4:方程式をたてる。
追いつくってことはさ、歩いた道のりが等しくなるってことだよね。
例えば、弟が1000m歩いたのに、兄が800mしか歩いていなかったら追いつくはずがないよね。
追いつくってことは2人の道のりは等しくなるので
50(x+4)=70x
という方程式がたてられるよ。
ステップ5:方程式を解く
最後にかっこ( )をふくむ方程式を解いてみよう。
50(x+4)=70x
50x+200=70x
50x-70x=-200
-20x =-200
x =10
解はx=10だね。xって兄が家を出発してから弟に追いつくまでの時間だったら、10分が答えになるよ。
一次方程式の利用「割合の問題」
一次方程式を利用して「割合の問題」を考えてみよう。方程式をやる前に少し割合の復習をしよう。
割合の復習
次の問題を考えてみよう。
①100円の30%は何円ですか?
100×0.3=30円
②x円の30%は何円ですか?
x×0.3=0.3x円
30%を0.3という小数にして計算しているけど、分数\(\frac{3}{10}\)をかけてもいいよ。
一次方程式を利用して「割合の問題」を解こう
問
あるクラスの生徒数は36人です。男子の40%と女子の25%は眼鏡をかけていて、その合計は12人です。クラスの男子の人数は何人ですか。
ステップ1:図でイメージする。
どういう状況かを図で確認しよう。

ステップ2:求めたいものを確認する。
問題をもう一度見てみよう。
(問)
あるクラスの生徒数は36人です。男子の40%と女子の25%は眼鏡をかけていて、その合計は12人です。クラスの男子の人数は何人ですか。
赤字のところが今回求めたいものだよね。一次方程式では、求めたいものを「x」と置くので、今回は
クラスの男子の人数をx人
とします。
ステップ3:表にまとめる
男子や女子の人数を表にまとめよう。今回は「男子」と「女子」と「合計」もあるから次のような表になるよ。(今回の問題で必要ないところは「・・・・」にしたよ)
| 男子 | 女子 | 合計 | |
| 人数(人) | ① | ② | 36 |
| 眼鏡の人の割合(%) | 40% | 25% | ・・・・ |
| 眼鏡の人の人数(人) | ③ | ④ | 12 |
①②に入るものを考えよう。
①クラスの男子の人数をxとしたので、①には「x」が入るよ。
②女子の人数を考えよう。
男子と女子の人数を合わせたら36人になるから、
女子の人数は36-x(人)と表されるね。
今の段階で表は次のようになっているよ。残るは③と④だね。
| 男子 | 女子 | 合計 | |
| 人数(人) | x | 36-x | 36 |
| 眼鏡の人の割合(%) | 40% | 25% | ・・・・ |
| 眼鏡の人の人数(人) | ③ | ④ | 12 |
③④に入るものを考えよう。
③④を求めるには、割合の考え方が必要になってくるよ。
③男子x人の40%が眼鏡をかけているので、その人数は
x×0.4=0.4x人
④女子(36-x)人の25%が眼鏡をかけているので、その人数は
(36-x)×0.25 ←分配法則を使ってかっこを外すよ。
=36×0.25-x×0.25
=9-0.25x
表をもう一度確認してみよう。
| 男子 | 女子 | 合計 | |
| 人数(人) | x | 36-x | 36 |
| 眼鏡の人の割合(%) | 40% | 25% | ・・・・ |
| 眼鏡の人の人数(人) | 0.4x | 9-0.25x | 12 |
ステップ4:方程式をたてる
男子で眼鏡をかけている人数と女子で眼鏡をかけている人数を足したら12人になるということは方程式は次のようになるよ。
0.4x+9-0.25x=12
ステップ5:方程式を解こう
小数をふくむ方程式を解いていこう。
0.4x+9-0.25x=12
小数を分数にするために、両辺を100倍しよう。
0.4x×100+9×100-0.25x×100=12×100
40x+900-25x=1200
40x -25x=1200-900
15x =300
x =20
解はx=20だね。xって男子の人数だったら、20人が答えになるよ。
まとめ
「一次方程式を利用した問題」はどうだったかな?
方程式をたてることが難しかったと思うよ。
方程式をたてて、答えを求めるための手順を下にまとめてみたよ。
①図でイメージする
②求めたいものを確認する
③表にまとめる
④方程式をたてる
⑤方程式を解く
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。




