①まだわかっていない数を表す文字
目次【本記事の内容】
「まだわかっていない数を表す文字」
教科書の説明をかんたんに解説
教科書の説明
場面や数量の関係を式に表すときに、□や○、△などの記号のかわりにχやα、bなどの文字を使うことがある。
まだわかっていない数をχなどの文字を使って式に表して、答えを求めることがある。
なんだかピンとこないね。
ひとつずつ「わかりやすい言葉」に通訳しながら解説するよ。
教科書場面や数量の関係を式に表すとき
「場面」とは？？
「場面」なんてピンとこない言い方だけど、
「あるシーン」と考えたらどうかな？
たとえば・・・
「太郎くんが八百屋にお使いにいって、トマトとじゃがいもを買った」
なんてシーンがあったりするよね。
「数量」とは？？
「数量」とは、あるものの数とか量のこと。
たとえば、
「1個125gのトマトが5個入った袋の重さ（袋の重さは抜く）」
とか
「1000円で買えるトマトの数」
とか・・
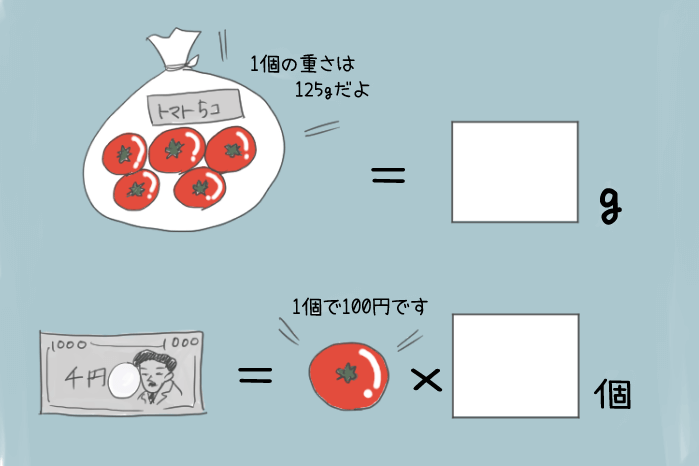
「場面や数量の関係を式に表すとき」というのは、こういう「シーン」とか「あるものの数や量」を、算数の「式」で表すとき
ということを言っているんだね。
続けるよ。
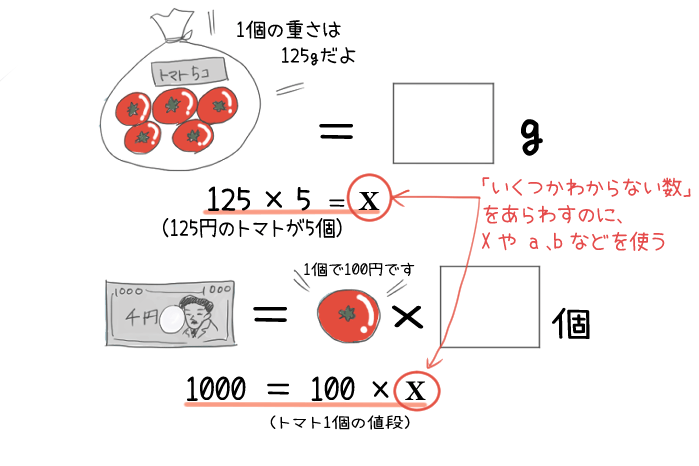
教科書□や○、△などの記号のかわりにχやα、bなどの文字を使うことがある。
くまごろうさっき言った「シーン」とか「あるものの数とか量」を、算数の式であらわすとき、その中に「χ」とか「α」とか「ｂ」のような「文字」を使うよ、ということだね。
たろう「□とか○とか△の代わり」ってどういうこと？
くまごろう実は「あるシーン」とか「あるものの数とか量」を算数の式であらわすという学習は小学3年生の算数でもすでにやっているんだ。
その時、式の中で「いくつなのかわからない数字」をあらわすために「□とか○、△」を使っていたんだよ。
たろうじゃあ3年生のときに使っていた「□とか○、△」の代わりに新しく「χ」とか「α」、「ｂ」という「文字」を使うよ 、というだけのことなんだね。
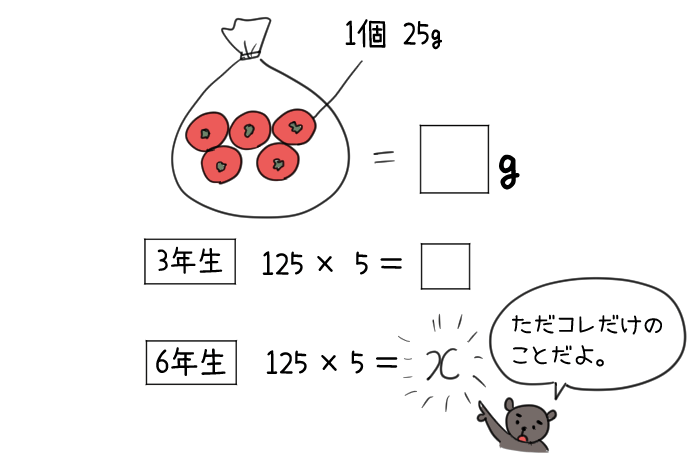
続けるよ。
教科書まだわかっていない数をχなどの文字を使って式に表して、答えを求めることがある。
くまごろうたとえばさっきの「シーン」、「太郎くんがお使いにいってトマトとじゃがいもを買った」と言ったけど、「トマトとじゃがいも、それぞれいくつ買ったのか」はナゾだよね。
ほかにも、「合計いくらだったのか」もナゾだね。
こういう、「まだわかっていない数」というのがあったとき、それはとりあえず「χ」とかの文字で表して計算して、答えを求めちゃおう、ということ を言っているんだよ。
たとえば、トマトがひとつ100円、じゃがいもはひとつ50円で10個買ったとして、お買いものの合計が1000円だったとするよね。
このとき、「トマトはいくつ買ったのか？」という答えを求めるとき、
「トマトを買った数」は「まだわかっていない数」だよね。
ということは、「トマトを買った数」を表すために「χ」を使う んだよ。
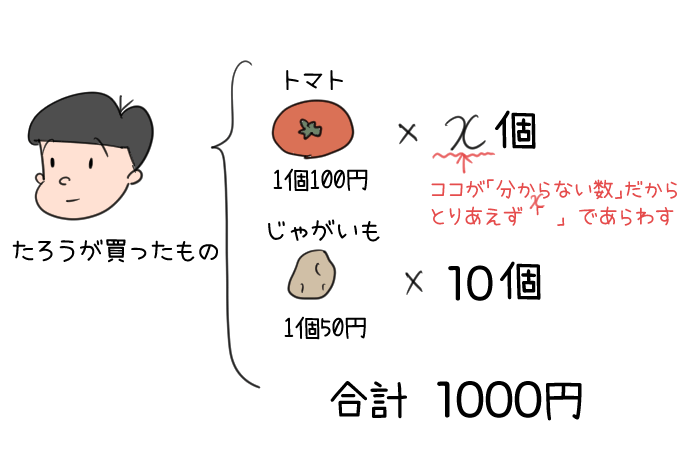
それでは実際に計算をして「χ」に当てはまる数字、つまり答えを求めてみよう！
たろううーんと、
トマトはひとつ100円だから、トマトを買った金額は「100円×トマトを買った数」だから「100×χ」だね！
じゃがいもの金額は「50円×10個」だから、「50×10」で「500」だね。
式にすると・・・
100χ＋500＝1000
（トマトの金額＋じゃがいもの金額＝1000円）
100χ＝1000一500
（トマトの金額は1000円一じゃがいもの金額）
100χ＝500
（トマトの金額は500円）
つまり、（1個100円のトマトをχ個買うと500円）
χ＝5
（トマトを買った数は5個）
「まだわかっていない数を表す文字」
どうして文字にするの？？
たろうでもさ、どうしていちいち文字にするの？そのままでも良さそうだし、もし置きかえるのでも□とか○じゃダメなの？
そのままで式にすると・・
くまごろう式がとっても長くなって大変だね。
いちいち書くのも面倒だよね。
「トマトを買った数」という言葉を「χ」という1文字で表すことができるなんてとっても便利だよね！
しかも、「まだわかっていない数」ならなんだっていいんだ。
もし「じゃがいもを買った数」が分からない場合でも使えるし、「合計金額」が分からない場合でも使える。
たろうなるほど。物を整理するときに、とりあえずなんでも入れておける便利なカゴみたいなイメージだね。
「まだわかっていない数を表す文字」
どうして「X」を使うの？？
□や○、△でも「まだわかっていない数」を表すことはできていたね
。
でも、3年生くらいの算数の問題ならそれで間に合ったけれど、6年生や中学、さらに高校となると、とても複雑な式を作ることになったりするんだ。
□や○、△を全部使ってしまって、まだ必要だったらどうする？
☆とか♡とか・・◎とか？
でも、手で式を描くのに、複雑な図形を描くのはそれだけで大変だね。
それよりも、アルファベットの「文字」で表したほうが、種類も26文字あるし、ハッキリ区別できるよね。
たろうでも、なんで「χ」なの？
くまごろうもちろん、「χ」じゃなくてもいいんだけど、キホン的には「まだわかっていない数」は「χ」を使うようになっているよ。
これには、色々説があるんだけど、一番正しいんじゃないか？と言われている説を紹介するね。
※余裕があったら読んでみよう！
どうして「χ」を使うのか？
フランスの数学者の「デカルト」という人は、「すでにわかっている数字」を文字で表すのに、アルファベットの最初から順番に「α」「ｂ」「ｃ」・・と表した。
逆に「まだわかっていない数」を文字で表すためにはアルファベットの最後から順番に「ｚ」「ｙ」「χ」・・と表すことにした。
デカルトの時代では、印刷するときに「活版印刷（かっぱんいんさつ）」という方法が使われていて、「活字（かつじ）」と呼ばれる文字ひとつひとつの版を並べて印刷していたんだ。
その時、「χ」はあまり使われる機会がなくて（つまり、χが入っている言葉がもともと少ない）、たくさん版が余っていたので、
「じゃあたくさん余っている「χ」を優先して使おうか」
ということで「χ」が使われるようになったという説があるよ。
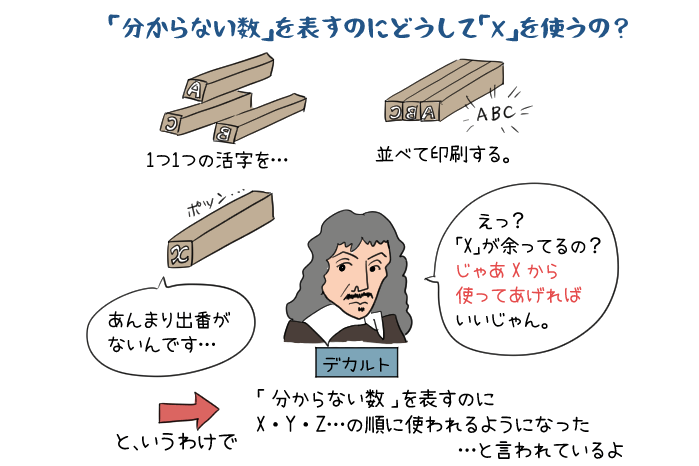
たろうということは、χが使われるようになった理由は「いっぱい余っていたから」なんだね…
くまごろうちなみに、 レントゲンで使われる「x線」ってあるよね。
この「x線」、発見したレントゲンが「未知のものを発見した！！」という意味を込めて「まだわからない＝x」ということで、「x線」と名付けたんだよ。
「まだわかっていない数を表す文字」では
どんな問題が出るのかチェックしよう！
ひとつ40円のチョコを4つと、ジュースを1本買った。
代金の合計は320円だった。
ジュース1本の金額はいくらか、「ジュース1本の金額」を「χ 」として式で表し、答えをもとめなさい。
くまごろう文字を使った式の答えかた、ポイントは「文章を式に変身させる」ことだよ。
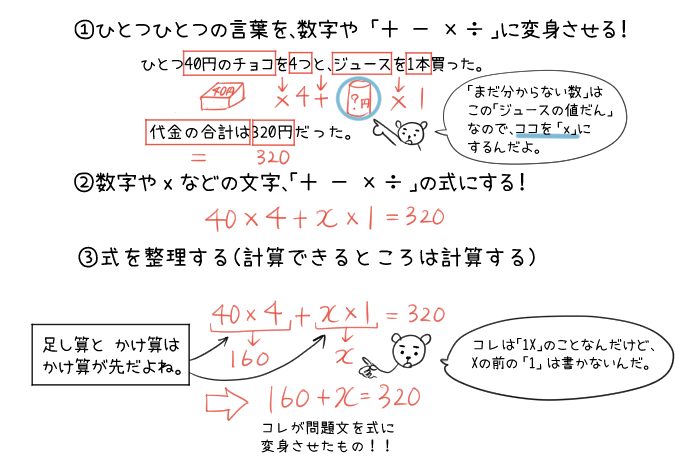
これで問題文から
160＋χ＝320
という式が出来たね。
あとはこの式のχをもとめればいいんだ。
χ＝320−160
χ＝160
答え：ジュース1本の値段は160円
6年生はココを押さえればOK！
「まだわかっていない数を表す文字」まとめ
ザックリいうと
「まだわかっていない数」が登場する問題では、これまでは□とか△なんかを使っていたけど、これからは「まだわかっていない数」を「χ」とか「α」、「ｂ」などの文字であらわすよ！ということ。
※赤いキーワードは必ず覚えよう！
- あるシーンや、ものの数や量の関係を表すときに、アルファベットの「χ」や「α」「ｂ」などの文字を使うことがある
- 「まだわかっていない数」を「χ」などの文字を使って式に表して答えを求めることがある。
yumineko次は「数量の関係を表す文字」について解説するよ！
コメント