「角柱の体積の求め方」公式と問題の解き方をわかりやすく解説
小学校6年生の算数で学習する「角柱の体積の求め方」について、角柱の体積を求める公式と、なぜそのように求めることができるのかをわかりやすく解説するよ。
角柱の体積の求め方を、公式を使って問題を解く方法をくわしく紹介するよ。
底面積とは
「底面積」とは、漢字の意味からもわかるとおり、「底面」の「面積」のことだよ。
底面とは、立体の「底」になる面のこと。
もう少しわかりやすく言うと
地面に接している面のことだよ。
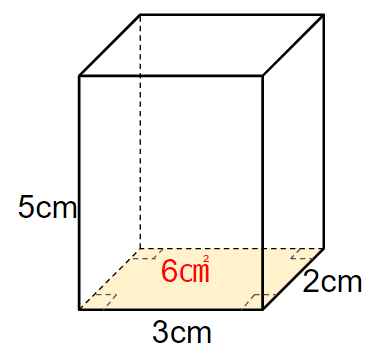
下の3つの立体だったら、黄色のところが底面になるよ。
※正確には立体の上面も「底面」と呼ばれるけれど、小学校6年生の算数では逆にわかりにくくなてしまうので、下の面だけを「底面」として考えるよ。
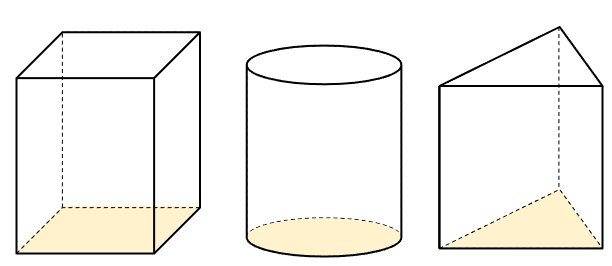
「底面積」とは、「底面の面積」のことだったね。
だから、上の図だと黄色の部分の面積のことを底面積というよ。
「底面積」は、体積を求めるときに絶対に必要になる知識だから、
どこが「底面積」になるのかをしっかり覚えておこうね。
角柱の体積の求め方の公式
「角柱」とは、三角柱や四角柱や五角柱など、「〇角柱」と呼ばれる立体をまとめた呼び方だよ。
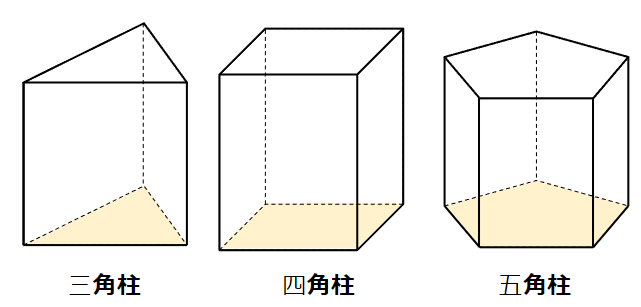
それでは角柱の体積の求め方の公式を考えてみよう。
「体積」とは、「その立体にどのくらい水が入るかを表したもの」だとイメージするとわかりやすいよ。
角柱の体積は、さっき確認した「底面積」に、その角柱の高さをかけることで求めることができるんだ。
角柱の体積の求め方の公式
- 底面積×高さ
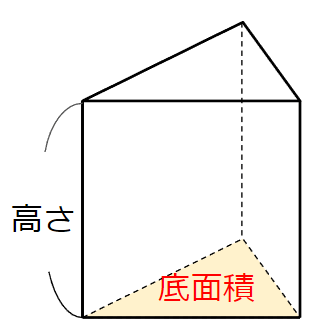
でも、なんで角柱の体積は「底面積×高さ」で求めることができるのかな?
角柱の体積の求め方の公式が成り立つ理由
100万円の札束を思い出してみて。
1枚1枚はとても薄い1万円札でも、100枚積み重なることで、立体になるよね。
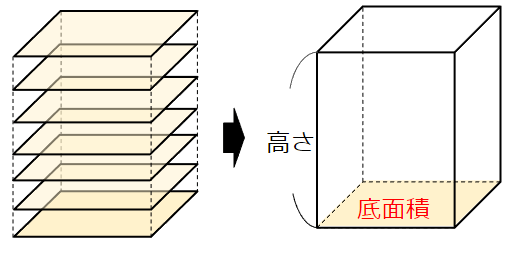
角柱も、同じ考え方をするんだ。
底面が、何枚も何枚も積み重なって、立体である角柱になっていると考えるんだよ。
たとえば下の三角柱を見てみよう。
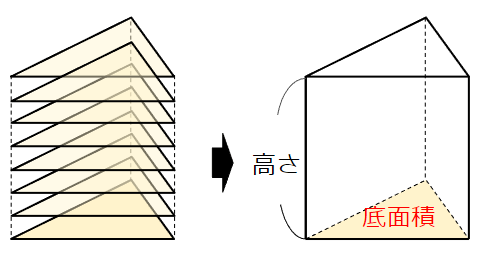
三角柱って、底面は三角形だよね。
その三角形が何枚も何枚も、角柱の高さ分積み重なって、三角柱が出来上がっているんだ。
底面の三角形が高さ分積み重なることで三角柱ができているのだから、
体積は「底面積×高さ」で求めることができるというわけだね。
他の角柱も同じ考えで、「底面積×高さ」の公式が成り立つよ。
- 四角形が高さ分積み重なって、四角柱が出来上がる
→体積は「底面積×高さ」で求められる。
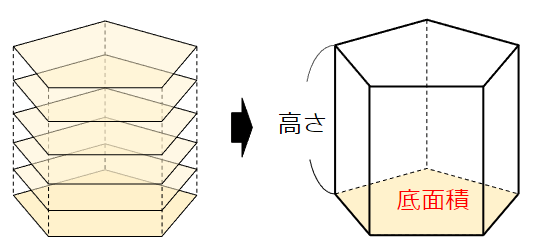
- 五角形が高さ分積み重なって、五角柱が出来上がる
→体積は「底面積×高さ」で求められる。
角柱の体積を求める問題
角柱の体積の求め方の公式「底面積×高さ」がわかったから、実際に公式を使って問題にチャレンジして慣れていこう。
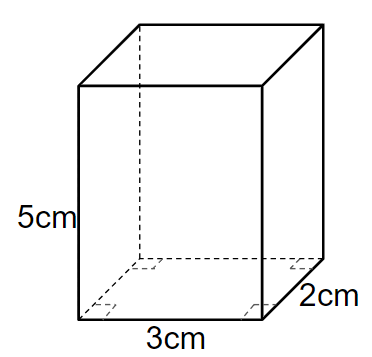
下の四角柱の体積を求めなさい。
〇角柱の体積は「底面積×高さ」だから、まずは底面積を考えよう。
STEP1 底面積を考えよう
四角柱の底面積は黄色のところだよね。
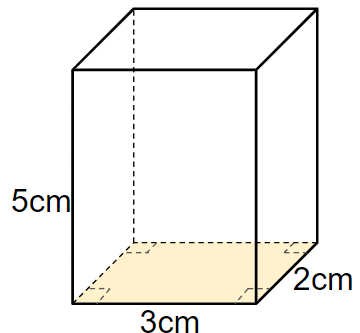
四角柱だから、底面は次のような四角形だよね。
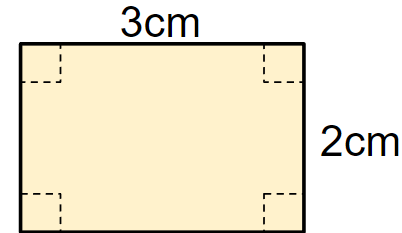
面積は(縦)×(横)で求まるから
底面積は2×3=6cm2になるよ。
STEP2 角柱の体積を求めよう
角柱の体積は
(底面積)×(高さ)で求まるから
6×5=30cm3
と計算できるね。
単位が「cmになっていることに注意しよう。
どうして「cmになるのかというと、これは「縦・横・高さの3つ」がかけ合わされているからだよ。
面積は、「縦と横の2つ」がかけ合わされているから、cm2なんだ。
今回はステップ1と2にわけて計算したけれど、
慣れてきたら
「底面積を求めて、高さをかける」
という計算を一発でできるようになると思うよ。
「縦×横×高さ」で、
2×3×5=30みたいなかんじだね。
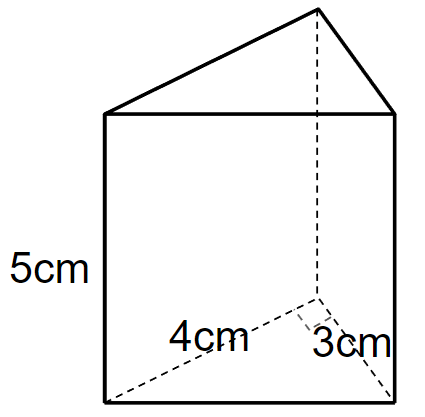
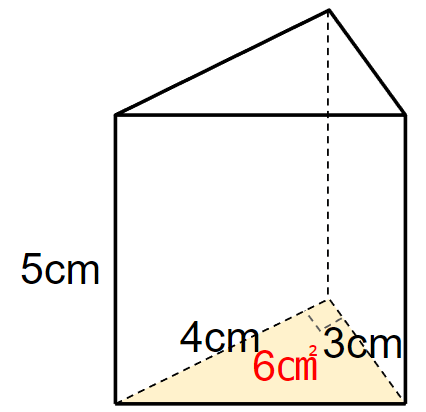
下の三角柱の体積を求めなさい。
〇角柱の体積は「底面積×高さ」だから、まずは底面積を考えよう。
STEP1 底面積を考えよう
三角柱の底面積は黄色のところだよね。
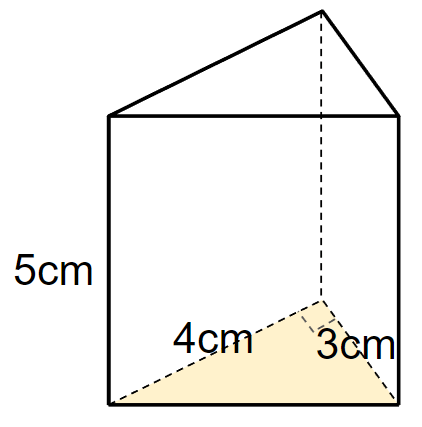
三角柱だから、底面は次のような三角形だよね。
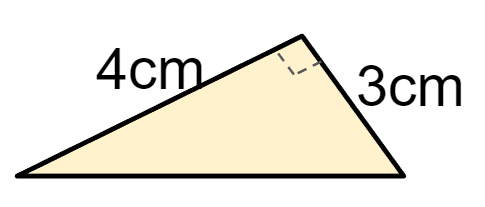
三角形の面積は(底辺)×(高さ)÷2で求まるから
底面積は4×3÷2=6cm2になるよ。
(底辺を3cmと考える場合は、3×4÷2=6cm2)
STEP2 角柱の体積を求めよう
角柱の体積は
(底面積)×(高さ)で求まるから
6×5=30cm3
と計算できるね。
下の五角柱は底面積が8cm2で高さが4cmです。
体積を求めなさい。
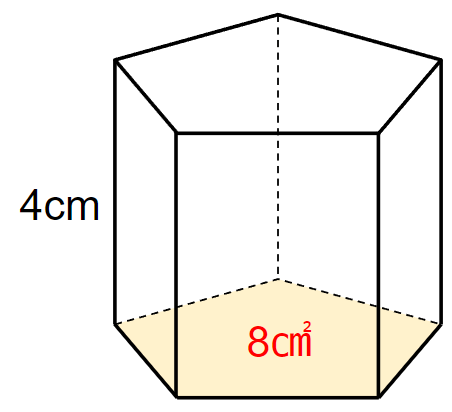
今回の問題はすでに底面積が求まっているね。
だから簡単に求めることができるよ。
角柱の体積は
(底面積)×(高さ)で求まるから
8×4=32cm3
と計算できるね。
角柱の体積の求め方のまとめ
角柱の体積の求め方 まとめ
- 立体の底になる面のことを底面という
- 底面の面積のことを底面積という
- 角柱(三角柱や四角柱など〇角柱)の体積は
角柱の体積を求める公式「底面積×高さ」で求めることができる
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。




さんこうになります