「分数と分数の掛け算」のやり方・逆数とはなにかわかりやすく解説
小学校6年生の算数で学習する「分数の掛け算」について、分数と分数の掛け算のやり方をわかりやすく解説するよ。
分数の掛け算や分数の割り算で使われる「逆数」とはなにか、くわしく紹介しているよ。
分数と分数の掛け算
今までは分数と整数の掛け算を学習してきたよね。
今回は分数と分数の掛け算のやりかたを学習するよ。
分数と分数の掛け算の考え方①
次の分数×分数のやり方を考えよう。
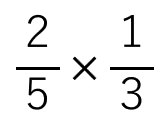
今まで、「分数×整数」「分数÷整数」の計算はやってきたよね。
だから、「分数×整数」「分数÷整数」の形に無理やり変えちゃうよ。
\(\frac{1}{3}\)を整数にするために、3をかけよう。
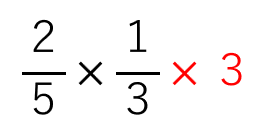
ただ、勝手に3をかけたら、計算の答えが変わっちゃうよね。
「2×1」を「2×1×3」にしちゃだめだよね。
だから、÷3もするよ。
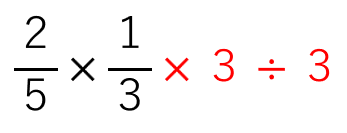
「×3」をして「÷3」をしたら「1」になるから、
赤の数字のところはなかったことになるよ。
ただ、こうやって式の形を変えると今までの知識が使えるんだ。
下の式で( )をつけた場所を見てみよう。
分数×整数の形になっているね。
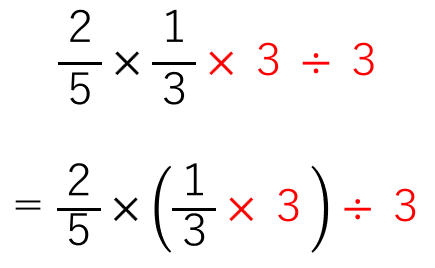
分数×整数のポイントは、
整数の数字が分子(上)に来ることだったから、
次のようになるよ。
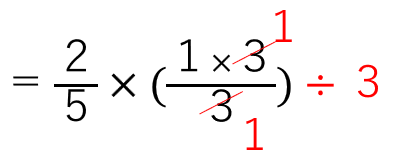
約分すると
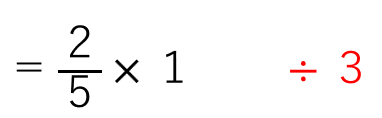
今度は、下の( )をつけた場所を見てみよう。
分数×整数になっているから、さっきと同じように計算すると
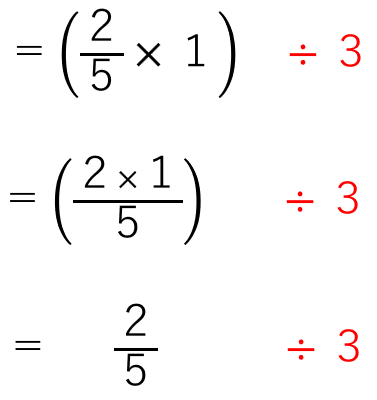
式が結構シンプルになったね。
最後は、分数÷整数の形になっているね。
分数÷整数の時は、
整数の数字を分母(下)に移動させて掛け算すればよかったから、
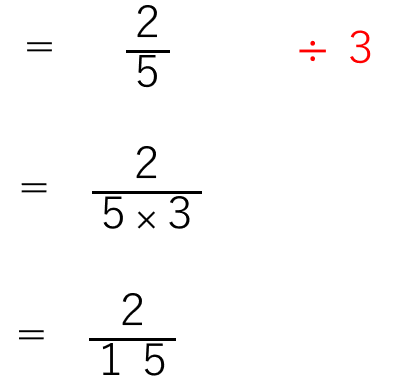
答えを求めることができたけど、
「うわー大変だ」「計算がめんどくさいな」と思ったよね。
実は、分数×分数の問題はもっと簡単に計算することができるんだよ。
最初の式と答えを見比べてみよう。
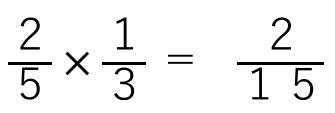
・分母の「5×3」が答えの15
・分子の「2×1」が答えの2
になっているね。
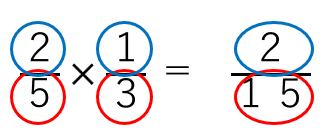
そう、分数×分数は、「分母同士」と「分子同士」を掛けてあげればいいんだ。
分数×分数のかけ算のポイント
- 分母同士、分子同士を掛ける
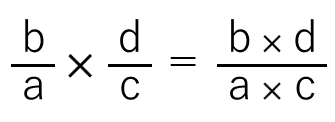
もう1つの考え方で、分数×分数の計算を考えてみよう。
分数と分数の掛け算の考え方②
図を使って考えてみよう。
下のように、1Lの水が入るタンクがあったとしよう。
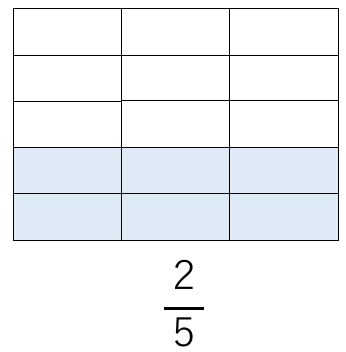
\(\frac{2}{5}\)っていうのは、
5個に分けたうちの2個分に水が入っているということになるよね。
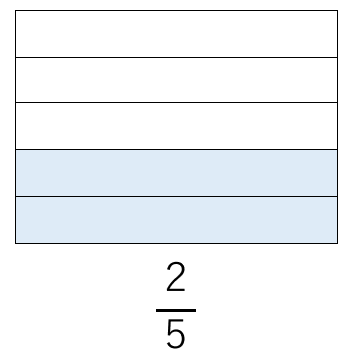
この後がポイントなんだけど、
\(\frac{2}{5}\)の水って次のようにも考えられるよね。
(1段を3つの部屋に分けたよ)
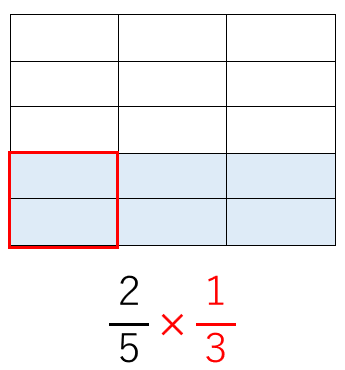
\(\frac{2}{5}\)×\(\frac{1}{3}\)っていうのは、
\(\frac{2}{5}\)の水の量を\(\frac{1}{3}\)にするイメージ
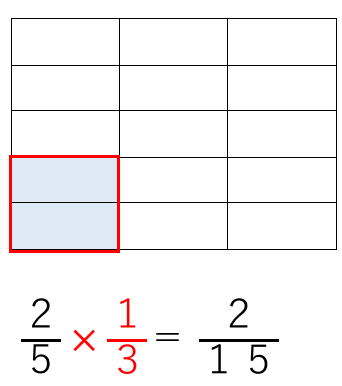
赤で囲った量って、15個に分けた2個分だよね。
だから\(\frac{2}{15}\)
とも表すことができるよ。
さっきと同じように
\(\frac{2}{5}\)×\(\frac{1}{3}\)=\(\frac{2}{15}\)
と計算することができたね。
逆数とは
分数の掛け算や割り算でよくでてくるのが、逆数という言葉だよ。
逆数というのは、「分母と分子を入れ替えた数」のこと。
例えば、次のようなイメージだよ。
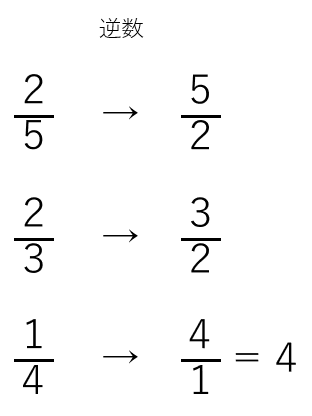
2の逆数はいくつだと思う?
2は、分数にしたら\(\frac{2}{1}\)だから、
逆数にすると\(\frac{1}{2}\)になるね。
0.3の逆数はいくつだと思う?
0.3は、分数にしたら\(\frac{3}{10}\)だから、
逆数にすると\(\frac{10}{3}\)になるね。
整数や小数を逆数にするときは、分数にしてから考えることがポイントだよ。
逆数とは
・分母と分子を入れ替えた数のこと
・整数や小数を逆数にするときは、分数にしてから考える
「分数と分数のかけ算」まとめ
分数×分数のかけ算のポイント
- 分母同士、分子同士を掛ける
逆数とは
- 分母と分子を入れ替えた数のこと
- 整数や小数を逆数にするときは、分数にしてから考える
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


