「比の利用と文章問題」比の問題の解き方をわかりやすく解説
小学校6年生の算数で学習する「比」について、比を利用した問題の解き方をわかりやすく解説するよ。
比の文章問題の考え方、「比の一方の量を求める方法」と「全体の量を、部分と部分の比で分ける方法」について、例題をもとにくわしく紹介していくよ。
比の一方の量を求める方法
今まで、等しい比の性質や比の値について勉強してきたね。
実は「比」って日常生活でもよく登場しているんだ。
たとえば次のようなことを考えることもあるよね。
コーヒーと牛乳を1:2で混ぜてコーヒー牛乳を作るとする。
コーヒーが30mLのとき、牛乳は何mL必要か?
「比」の性質を利用しなくても、「牛乳は60mLだね。」とわかる人もいるかもしれないね。
でも、せっかく比について学習したのだから、今回は比の性質を使って次の2つのやり方で求めてみよう。
等しい比の性質を使って求める方法
等しい比の性質は次の通りだったね。
等しい比の性質
- 両方の数に同じ数をかけても等しい
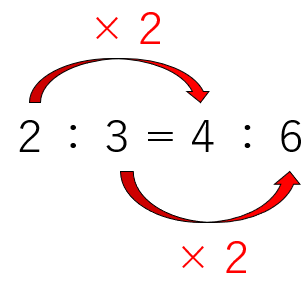
- 両方の数を同じ数でわっても等しい
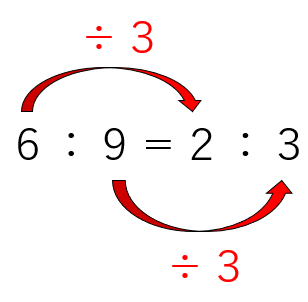
この性質を使って、答えを求めてみよう。
さっきの問題文を図にすると次のようになるよ。
牛乳の量をxmLとしたよ。
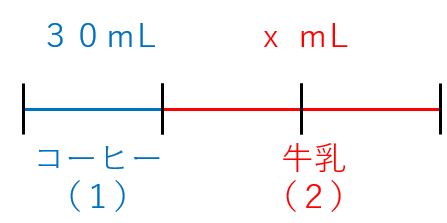
この図から、比の関係を式にすると
- コーヒー:牛乳=1:2
- コーヒー:牛乳=30:x
2つの式を合体させると
コーヒー:牛乳=1:2=30:x
ここで
等しい比の性質「両方の数に同じ数をかけても等しい」を使おう。
コーヒーは1から30で30倍になっているから、
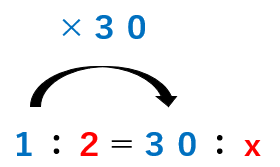
牛乳も2を30倍したらxになるよね。
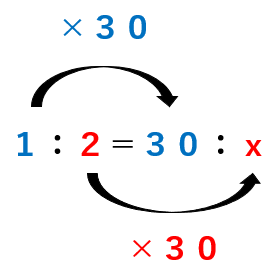
だから
x=2×30
=60
牛乳の量は60mLと求めることができたね。
比の値を使って求める方法
等しい比の性質ではなく、比の値を使って求めることもできるんだ。
比の値の求め方
a:bの比の値は\(\frac{a}{b}\)とあらわすことができる。
コーヒー:牛乳=1:2
だから、比の値は1÷2=\(\frac{1}{2}\)だね。
つまり、
コーヒーは牛乳の\(\frac{1}{2}\)ということ。
牛乳の\(\frac{1}{2}\)がコーヒー30mLだから、
牛乳は30×2=60mLと求めることできるね。
全体の量を、部分と部分の比で分ける方法
さっきは、「2つを混ぜるところ、片一方の量がわからない」という問題だったね。
今度は全体の量がわかっている問題の解き方を確認していこう。
コーヒー牛乳を1200mL作るとする。
コーヒー:牛乳を3:2で混ぜるとき、牛乳は何mL必要か?
今回も2つの解き方で確認していこう。
等しい比の性質を使って求める方法
さっきの問題文を図にすると次のようになるよ。
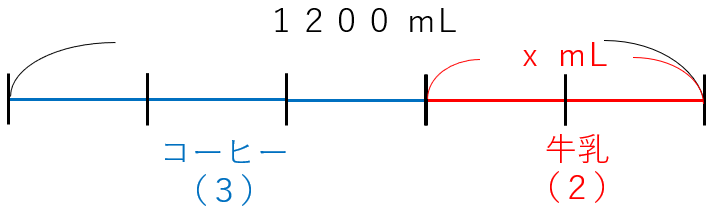
前の問題と同じように、
「コーヒー:牛乳=・・・」みたいな式を作っても
答えを求めることはできないよ。
だって、今回わかっているのは全体の量だからね。
だから全体の量について式にするといいよ。
- 全体:牛乳=(3+2):2
- 全体:牛乳=1200:x
2つの式を合体させると
全体:牛乳=5:2=1200:x
全体は5から1200で240倍になっているから
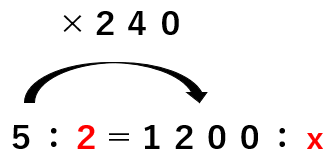
牛乳も2を240倍すればxが求まるね。
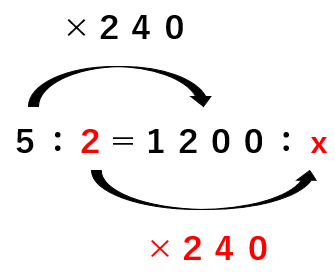
だから
x=2×240
=480
牛乳の量は480mLと求めることができたね。
比の値を使って求める方法
等しい比の性質ではなく、比の値を使って求めることもできるよ。
全体:牛乳=5:2
だから、比の値は5÷2=\(\frac{5}{2}\)だね。
つまり、
全体は牛乳の\(\frac{5}{2}\)ということ。
全体のコーヒー牛乳の量が1200mLで、
求めたい牛乳の量をxmLとすると
x×\(\frac{5}{2}\)=1200
xを求めると次のようになるよ。
x=1200÷\(\frac{5}{2}\)
x=1200×\(\frac{2}{5}\)
x=480
牛乳は480mLと求めることできるね。
比の利用の文章問題(練習問題)
それでは、練習問題に挑戦してみよう。
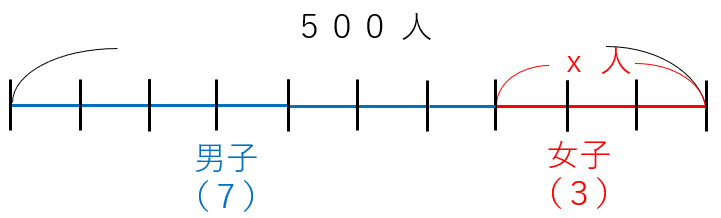
ある学校の生徒数は500人で、男女の比は7:3である。
女子の人数を求めなさい。
「全体の人数」がわかっている問題だね。
等しい比の性質を使って答えを求めよう。
問題文を図にすると次のようになるよ。
比の関係を式にすると
- 全体:女子=(7+3):3
- 全体:女子=500:x
2つの式を合体させると
全体:女子=10:3=500:x
全体は10から500で50倍になっているから
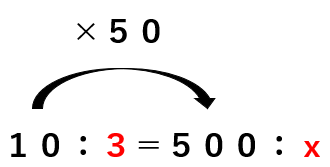
女子も3を50倍したらxが求まるね。
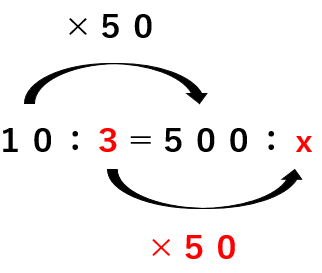
だから
x=3×50
=150
女子の人数が150人と求めることができたね。
ケーキを作るために、砂糖と小麦粉を7:3の割合で混ぜるとする。
砂糖が42gのとき、小麦粉は何g入れたらよいか。
「比の一方の量」を求める問題だね。
比の値を使って答えを求めよう。
砂糖:小麦粉=7:3
だから、比の値は7÷3=\(\frac{7}{3}\)だね。
つまり、
砂糖は小麦粉の\(\frac{7}{3}\)倍ということ。
砂糖42gで、小麦粉をxgとすると
x×\(\frac{7}{3}\)=42
xを求めると次のようになるよ。
x=42÷\(\frac{7}{3}\)
x=42×\(\frac{3}{7}\)
x=18
小麦粉は18gと求めることできるね。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



難しい