点対称な図形の書き方(コンパスを使ったマスなしの書き方も解説)
小学校4年生の算数で学習する「点対称な図形」について、マスを使って点対称な図形を書く方法、マスなしでコンパスを使って点対称な図形を書く方法をわかりやすく解説するよ。
点対称な図形の書き方(マスあり)
点対称な図形って、180°回転させたとき、もとの図形にピッタリ重なる図形のことだったよね。
点対称の図形を書くときは「対称の中心の性質」を使うから、忘れている人は復習しておこう。
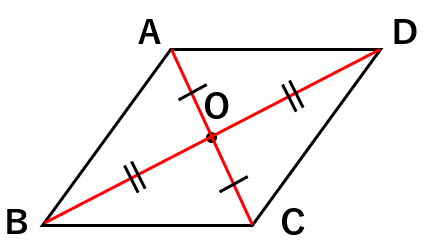
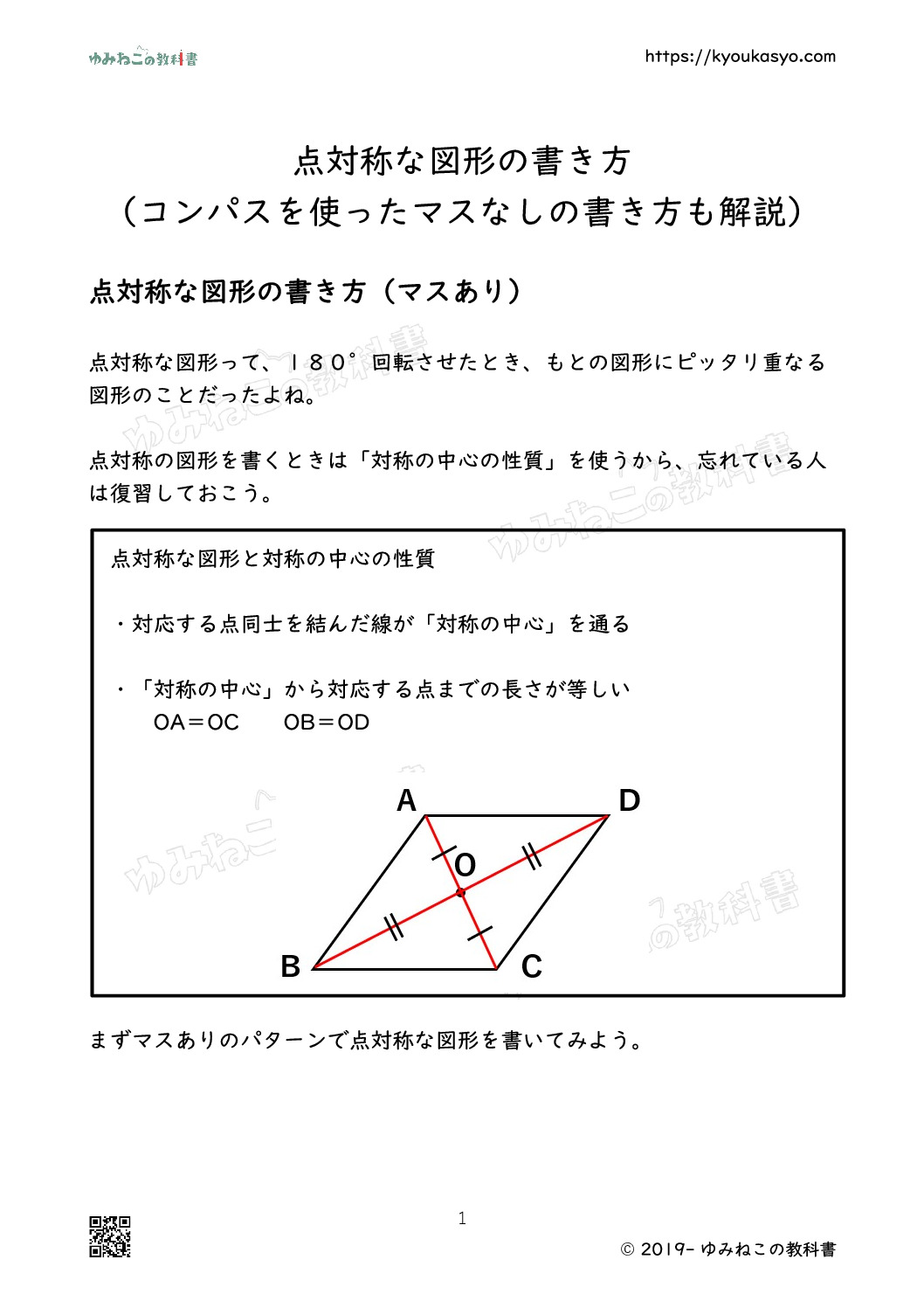
点対称な図形と対称の中心の性質
- 対応する点同士を結んだ線が「対称の中心」を通る
- 「対称の中心」から対応する点までの長さが等しい
OA=OC OB=OD
まずマスありのパターンで点対称な図形を書いてみよう。
点対称な図形を書こう(マスあり)
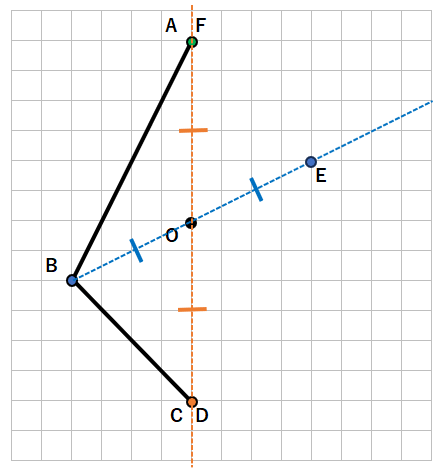
下の図と点対称な図形を書きなさい。(点Oは対称の中心)
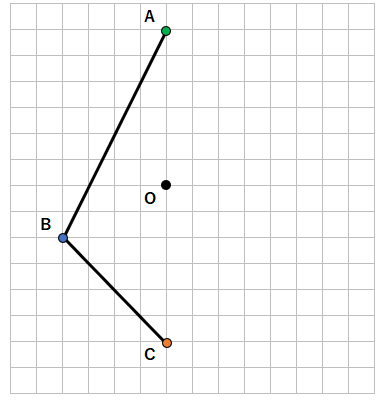
STEP1 点Aと対応する点を結んだ線が「対称の中心」を通る性質を使おう
点Aと対応する点を結んだ線が「対称の中心O」を通るから、まず、点Aから点Oを通る線を引こう。
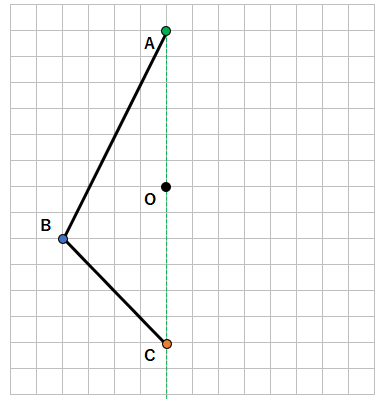
緑の線のどこかに、点Aに対応する点があるってことだよ。じゃあ、STEP2で、点Aに対応する点を見つけよう。
STEP2「対称の中心」から対応する点までの長さが等しい性質を使おう
「対称の中心O」から
上に6マスのところに点Aがあるから、
下に6マスのところが点Dになるよ。(今回の図形では、点Cと同じところになるね。)
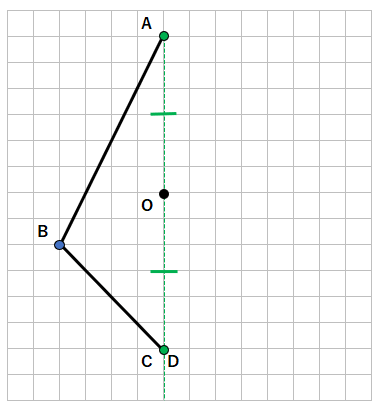
点Aに対応する点を探したような感じで、点Bと点Cもやってみよう。
STEP3 点Bと対応する点を結んだ線が「対称の中心」を通る性質を使おう
点Bと対応する点を結んだ線が「対称の中心O」を通るから、まず、点Bから点Oを通る線を引こう。
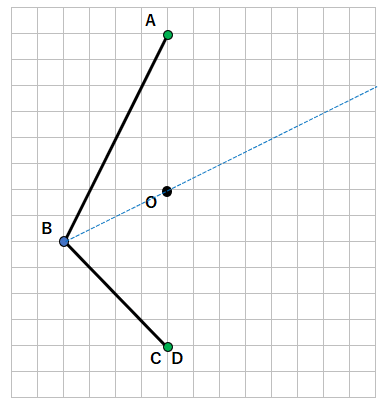
青の線のどこかに、点Bに対応する点があるってことだよ。じゃあ、STEP4で、点Bに対応する点を見つけよう。
STEP4「対称の中心」から対応する点までの長さが等しい性質を使おう
「対称の中心O」から
左に4マス、下に2マスのところに点Bがあるから、
右に4マス、上に2マスのところが点Eなるよ。
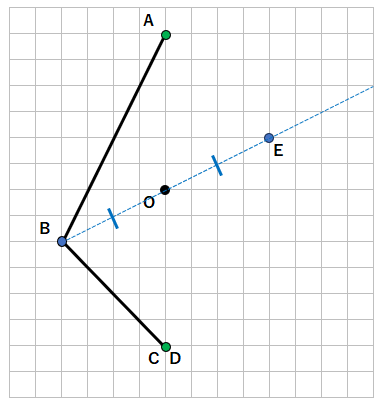
最後に点Cについて考えてみよう。
STEP5 点Cと対応する点を結んだ線が「対称の中心」を通る性質を使おう
点Cと対応する点を結んだ線が「対称の中心O」を通るから、まず、点Cから点Oを通る線を引こう。
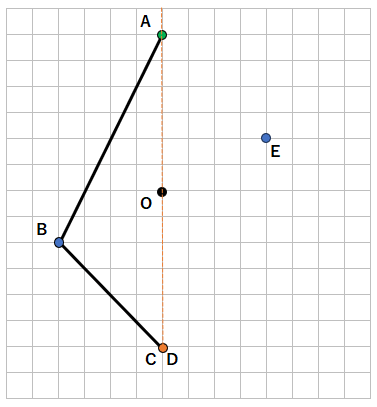
黄色の線のどこかに、点Cに対応する点があるってことだよ。じゃあ、STEP6で、点Cに対応する点を見つけよう。
STEP6「対称の中心」から対応する点までの長さが等しい性質を使おう
「対称の中心O」から
下に6マスのところに点Cがあるから、
上に6マスのところが点Fになるよ。(今回の図形では、点Aと同じところになるね)
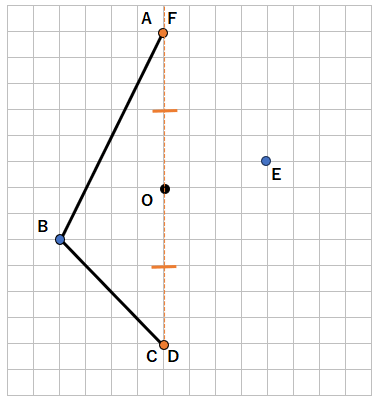
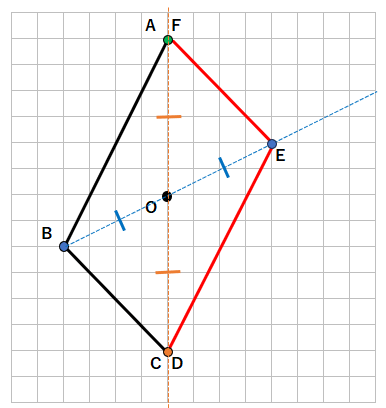
STEP7 点を結ぼう
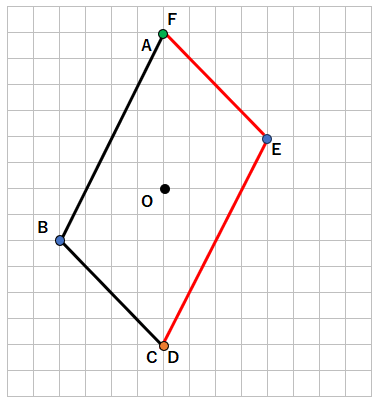
点D、点E、点Fを結ぶと次のようになるよ。これが点対称な図形だね。
点対称な図形の書き方(マスなし・コンパス使用)
今まではマス目があったけど、次はマス目なしバージョンの書き方を確認しよう。ぶっちゃけ、マス目があってもなくても、難しさは変わらないよ。
ただ、マス目なしバージョンではコンパスを使うから準備しておこう。
点対称な図形を書こう(マスなし・コンパス使用)
次の図の点対称な図形を書きなさい。(点Oは対称の中心)
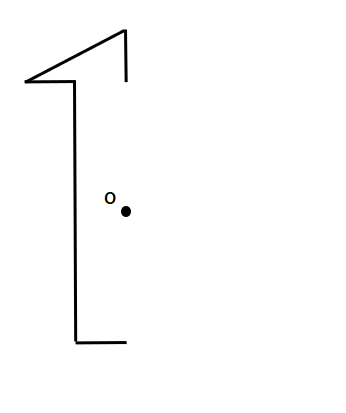
説明をわかりやすくするために、点A~点Eに色の印をつけたよ。
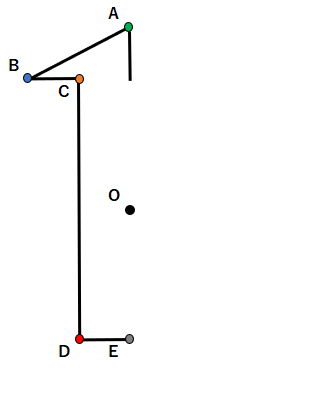
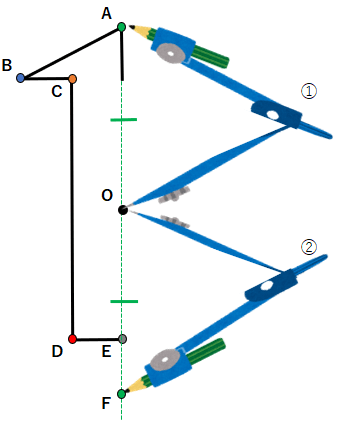
STEP1 点Aと対応する点を見つける
まず、対応する点同士を結んだ線が「対称の中心」を通るから、点Aから点Oを通る線を引こう。
次にコンパスを使って、同じ長さを測ろう。
- 点Oにコンパスの針をさして、点Aに鉛筆を当てる。(図①)
- コンパスの大きさは変えずに、点Aと反対側の緑色の線に印をつける。(図②)
- 印をつけたところが、点Aと対応する点F。
STEP2 点Bと対応する点を見つける
対応する点同士を結んだ線が「対称の中心」を通るから、点Bから点Oを通る線を引こう。
次にコンパスを使って、同じ長さを測ろう。
- 点Oにコンパスの針をさして、点Bに鉛筆を当てる。
- コンパスの大きさは変えずに、点Bと反対側の青色の線に印をつける。
- 印をつけたところが、点Bと対応する点G。
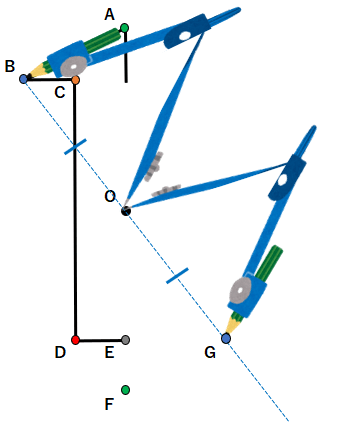
STEP3 点Cと対応する点を見つける
対応する点同士を結んだ線が「対称の中心」を通るから、点Cから点Oを通る線を引こう。
次にコンパスを使って、同じ長さを測ろう。
- 点Oにコンパスの針をさして、点Cに鉛筆を当てる。
- コンパスの大きさは変えずに、点Cと反対側の黄色の線に印をつける。
- 印をつけたところが、点Cと対応する点H。
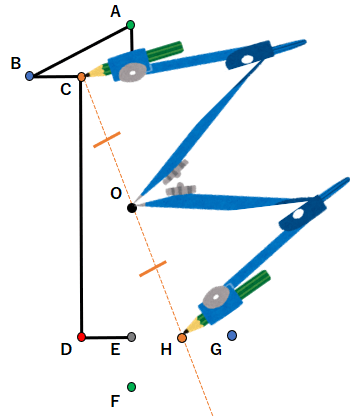
STEP4 点Dと対応する点を見つける
対応する点同士を結んだ線が「対称の中心」を通るから、点Dから点Oを通る線を引こう。
次にコンパスを使って、同じ長さを測ろう。
- ・点Oにコンパスの針をさして、点Dに鉛筆を当てる。
- ・コンパスの大きさは変えずに、点Dと反対側の赤色の線に印をつける。
- ・印をつけたところが、点Dと対応する点I。
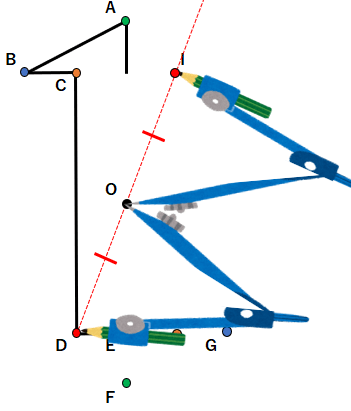
STEP5 点Eと対応する点を見つける
対応する点同士を結んだ線が「対称の中心」を通るから、点Eから点Oを通る線を引こう。
次にコンパスを使って、同じ長さを測ろう。
- 点Oにコンパスの針をさして、点Eに鉛筆を当てる。
- コンパスの大きさは変えずに、点Eと反対側の灰色の線に印をつける。
- 印をつけたところが、点Eと対応する点J。
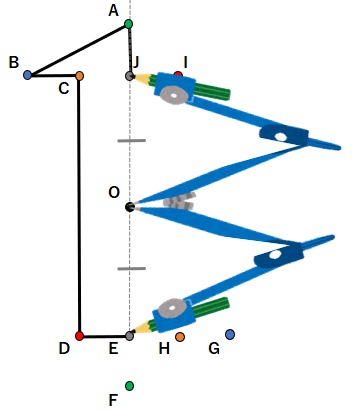
STEP6 点を線で結ぼう
STEP1~5で、次のような点を取ることができたね。
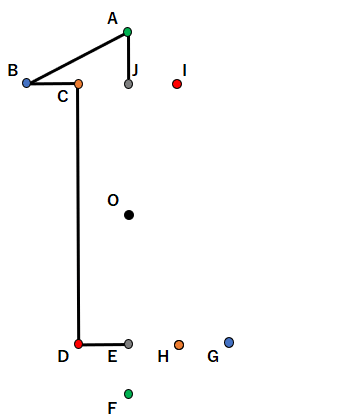
この点を線で結んでいくんだけど、どことどこを結ぶかってすごく大切だよ。適当に結ぶわけではないからね。
まず、辺ABを見てみよう。
点Aは緑、点Bは青だから、右下でも緑と青をつなごう。
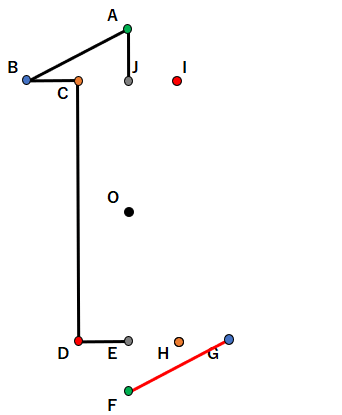
こんな感じで、結んでいくと次のような図形が完成するよ。
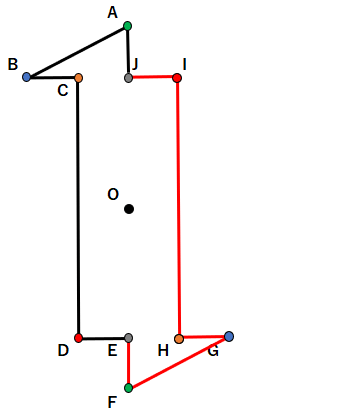
点対称な図形の書き方のまとめ
マス目がある場合もない場合も点対称な図形の書き方は次の通りだよ。
- 点と対称の中心を線で結ぶ
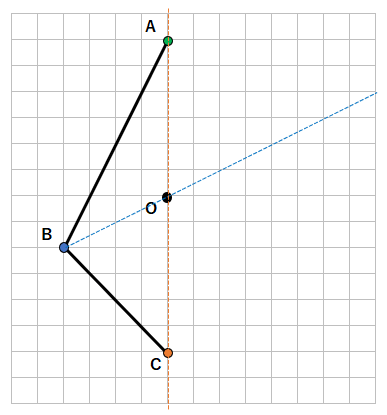
- 点と対称の中心と長さが等しいところが対応する点になる
マス目がない場合は、コンパスで等しい長さを測る
- 対応する点同士を結ぶ
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

-
-
分かりやすく点対称の書き方を教えてくれて、ありがとうございました。
いいテスト前の復習になりました。
-
-
とてもわかりやすくて、テスト前の復習にもなりました。ありがとうございます。
-
とても分かりやすかったのですが問題の図形が違い、あまり参考にはなりませんでした。

わかりやすくて、わからない問題もわかるようになりました
ありがとうございました!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1!!!!!!!