「分数と計算のきまり」帯分数・3つの分数の掛け算のやり方を解説

小学校６年生の算数で学習する「分数と分数の掛け算」のうち、帯分数の掛け算、分数×分数×分数（３つの分数の掛け算）などのやり方を、「計算のきまり」を使って解説するよ。

いろいろな分数の掛け算の例題の解き方を、わかりやすく紹介していくよ。

「分数と計算のきまり」 帯分数・3つの分数の掛け算のやり方を解説のPDF（12枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 分数と計算のきまり
• 基本の分数の掛け算
• 約分をしてから計算する分数の掛け算
• 帯分数の掛け算
• 分数×分数×分数（３つの分数）の掛け算
• 分数×整数の掛け算
• 「分数と計算のきまり」まとめ

分数と計算のきまり

分数×分数の計算のきまりは、
分母同士、分子同士を掛けるってことだったよね。
小学校だけではなく、中学、高校と必要な知識だからしっかり覚えておこう。

分数×分数のかけ算のポイント

• 分母同士、分子同士を掛ける

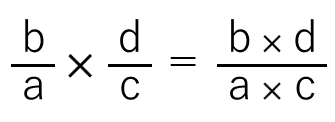
他にも分数の計算のきまりがあるから確認しておこう。

分数の計算のきまり

結論からいうと、次のようなきまりがあるよ。
整数や小数の時と同じだね。

①を見てみよう。
\(\frac{１}{３}\)×\(\frac{１}{２}\)も
\(\frac{１}{２}\)×\(\frac{１}{３}\)も
答えは同じになるよね。

②を見てみよう。
（\(\frac{１}{３}\)×\(\frac{１}{２}\)）×\(\frac{１}{４}\)のように
先に前２つの分数を掛け算しても

\(\frac{１}{３}\)×（\(\frac{１}{２}\)×\(\frac{１}{４}\)）
先に後ろ２つの分数をかけ算しても

答えは変わらないよ。

③を見てみよう。
次のような式を考えてみよう。

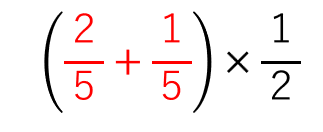
普通に（　）の中を足し算すると次のようなやり方になるよ。

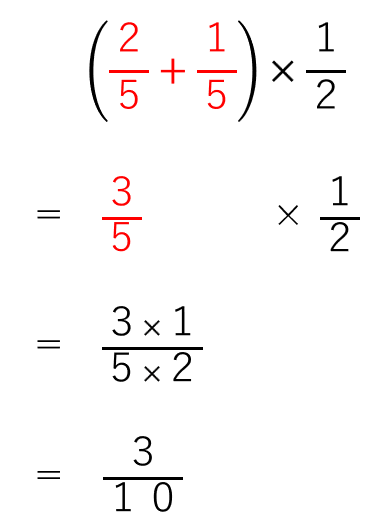
この計算を
③（ａ＋ｂ）×ｃ＝ａ×ｃ＋ｂ×ｃ
のきまりを使ってやってみよう。

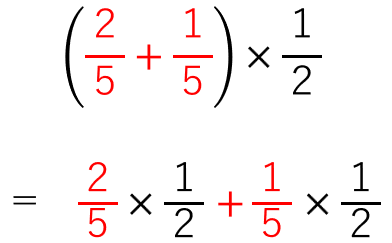
×\(\frac{１}{２}\)を前と後ろに分けて配るイメージだね。
だから、このきまりのことを「分配法則ぶんぱいほうそく」っていうよ。

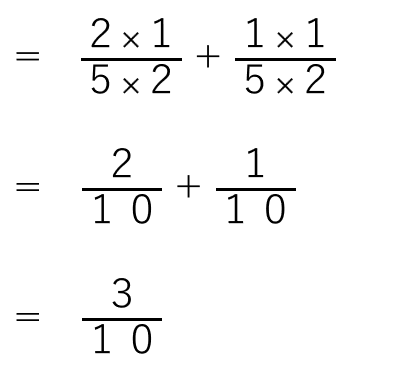
④を見てみよう。

次のような式を考えてみよう。

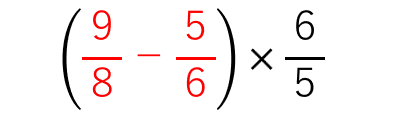
この計算を
④（ａ－ｂ）×ｃ＝ａ×ｃ－ｂ×ｃ
のきまりを使ってやってみよう。

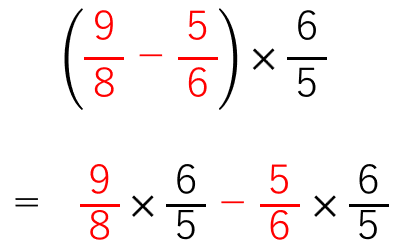
×\(\frac{６}{５}\)を前と後ろに分けて配るイメージだね。

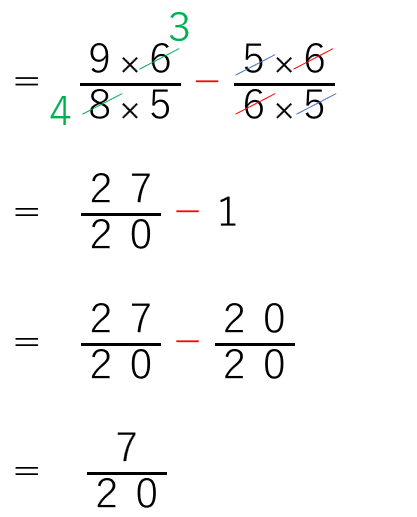
①～④の計算のきまりが分数でも成り立つことが確認できたね。
最後にもう一度①～④のきまりと、分数×分数のポイントを紹介するね。

分数×分数のかけ算のポイント

• 分母同士、分子同士を掛ける

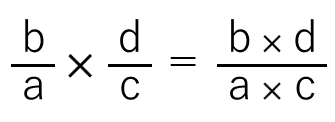
これらのきまりやポイントを使って、練習問題に挑戦しよう。

基本の分数の掛け算

分母同士、分子同士を掛ければよかったから、
\(\frac{１}{３}\)×\(\frac{１}{４}\)
＝\(\frac{１×１}{３×４}\)
＝\(\frac{１}{１２}\)

分母同士、分子同士を掛ければよかったから、
\(\frac{３}{７}\)×\(\frac{３}{４}\)
＝\(\frac{３×３}{７×４}\)
＝\(\frac{９}{２８}\)

約分をしてから計算する分数の掛け算

分母同士、分子同士を掛ければよかったから、
\(\frac{８}{９}\)×\(\frac{３}{４}\)
＝\(\frac{８×３}{９×４}\)
＝\(\frac{２４}{３６}\)

これで終わりではないよ。だって約分できるからね。
\(\frac{２４}{３６}\)　　分母と分子を４で割ろう
＝\(\frac{６}{９}\)　　　分母と分子を３で割ろう
＝\(\frac{２}{３}\)

約分が大変だったね。
ただ、計算のとちゅうで約分する方法があるよ。
\(\frac{８}{９}\)×\(\frac{３}{４}\)
＝\(\frac{８×３}{９×４}\)

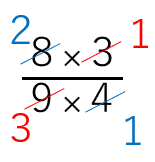
＝\(\frac{２×１}{３×１}\)
＝\(\frac{２}{３}\)

計算のとちゅうで約分した方が簡単に答えを求められるね。

分母同士、分子同士を掛ければよかったから、
\(\frac{５}{１２}\)×\(\frac{４}{５}\)
＝\(\frac{５×４}{１２×５}\)

約分しよう。

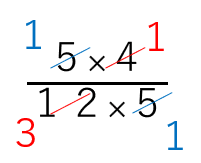
＝\(\frac{１×１}{３×１}\)
＝\(\frac{１}{３}\)

帯分数の掛け算

帯分数は仮分数に直してから掛け算しよう。
２\(\frac{１}{２}\)→\(\frac{５}{２}\)

\(\frac{１}{３}\)×２\(\frac{１}{２}\)
＝\(\frac{１}{３}\)×\(\frac{５}{２}\)
＝\(\frac{１×５}{３×２}\)
＝\(\frac{５}{６}\)

帯分数は仮分数に直してから掛け算しよう。
１\(\frac{１}{２}\)→\(\frac{３}{２}\)

\(\frac{２}{３}\)×１\(\frac{１}{２}\)
＝\(\frac{２}{３}\)×\(\frac{３}{２}\)
＝\(\frac{６}{６}\)
＝１

分数×分数×分数（３つの分数）の掛け算

今までは２つの分数の掛け算までだったけれど、３つの分数の掛け算の計算を紹介するね。
２つのときとやり方は同じだからね。

分母同士、分子同士を掛ければよかったから、
\(\frac{５}{１２}\)×\(\frac{４}{５}\)×\(\frac{３}{４}\)
＝\(\frac{５×４×３}{１２×５×４}\)

＝\(\frac{１×１×１}{１×１×４}\)
＝\(\frac{１}{４}\)

分母同士、分子同士を掛ければよかったから、
\(\frac{２}{３}\)×\(\frac{１}{４}\)×\(\frac{３}{２}\)
＝\(\frac{２×１×３}{３×４×２}\)

＝\(\frac{１×１×１}{１×４×１}\)
＝\(\frac{１}{４}\)

分数×整数の掛け算

分数×整数の掛け算は、
整数の数字を分子（上）に移動させて掛け算すればできるんだけど、
整数を分数に変えて計算する方法でやってみよう。

２って、分数に直したら、\(\frac{２}{１}\)だよね。

ってことは、
\(\frac{４}{５}\)×２
＝\(\frac{４}{５}\)×\(\frac{２}{１}\)
になって、分数×分数の式になったね。

あとは、分母は分母同士、分子は分子同士で掛け算して
\(\frac{４×２}{５×１}\)
＝\(\frac{８}{５}\)
と求められるよ。

３って、分数に直したら、\(\frac{３}{１}\)だよね。

ってことは、
３×\(\frac{４}{３}\)
＝\(\frac{３}{１}\)×\(\frac{４}{３}\)
になって、分数×分数の式になったね。

あとは、分母は分母同士、分子は分子同士で掛け算して
\(\frac{３}{１}\)×\(\frac{４}{３}\)

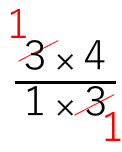
＝\(\frac{１×４}{１×１}\)
＝４
と求められるよ。

もちろん、（　　）の中を通分してから計算してもできるけど
通分するのは大変だよね。

だから、分配法則「③（ａ＋ｂ）×ｃ＝ａ×ｃ＋ｂ×ｃ」を使おう。
（\(\frac{１}{３}\)＋\(\frac{１}{４}\)）×１２
＝\(\frac{１}{３}\)×１２＋\(\frac{１}{４}\)×１２

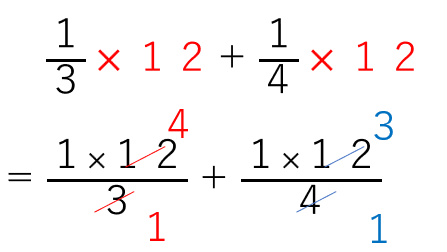
＝４＋３
＝７

（　　）の中を通分するよりも速く計算できるよね。

もちろん、（　　）の中を通分してから計算してもできるけど
通分するのは大変だよね。

だから、分配法則「③（ａ＋ｂ）×ｃ＝ａ×ｃ－ｂ×ｃ」を使おう。
（\(\frac{２}{５}\)－\(\frac{１}{４}\)）×２０
＝\(\frac{２}{５}\)×２０－\(\frac{１}{４}\)×２０

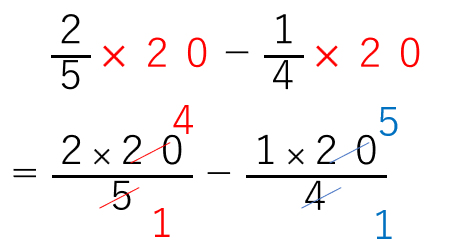
＝８－５
＝３

「分数と計算のきまり」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。