複雑な形の立体の体積の求め方（階段型・凹型・バームクーヘン型）

小学校６年生の算数で学習する「立体の体積」について、四角柱や三角柱、円中とはちがった複雑な形の立体の体積の求め方を解説するよ。

階段型、凹型の立体やバームクーヘンのような形の立体など、テストでもよく出てくるものを紹介していくよ。

複雑な形の立体の体積の求め方 （階段型・凹型・バームクーヘン型）のPDF（11枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 階段の形の立体の体積の求め方
• 複雑な形（凹の形）の立体の体積の求め方
• 複雑な形（バームクーヘン）の立体の体積の求め方
• まとめ

四角柱や三角柱、円柱などの基本的な立体の体積の求め方を学習してきたね。

テストでは、これらの基本的な立体のほかに、複雑な形をいた立体の体積をもとめる問題が出てきたりするよ。

ぱっと見ると「こんな立体の体積なんて、求められないよ！」と思ってしまうかもしれないけれど、コツをつかめば簡単に求められるようになるので、ひとつずつ確認していこう。

階段の形の立体の体積の求め方

まず紹介するのは、「階段のような形の立体」。
テストでもよく出てくる形のひとつだよ。

下の立体を縦に切って、体積を求めよう。

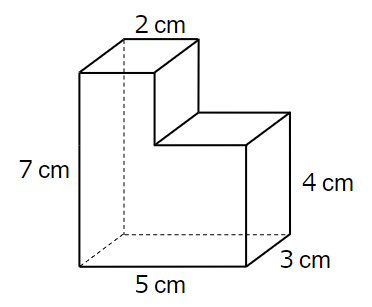
複雑な立体の体積をもとめるコツは、「知っている形になおす」こと。

この階段の形の立体も、これまで学習してきた知っている形になおしてみよう。
階段の形の立体は、２つの四角柱に分けることができるんだ。
分けかたは、「縦」と「横」の２とおりがあるよ。
ひとつずつ紹介するね。

縦に切って左右に分ける

知っている形（四角柱）になおすために、赤線のように縦に切ってみるよ。

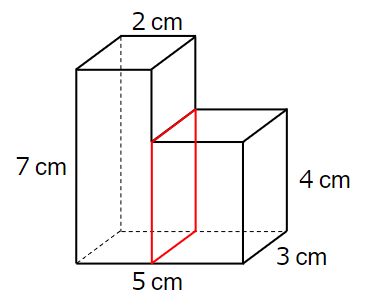
そうすると左右の四角柱に分けることができるね。
左も右も四角柱だから簡単に体積を求めることができるよね。

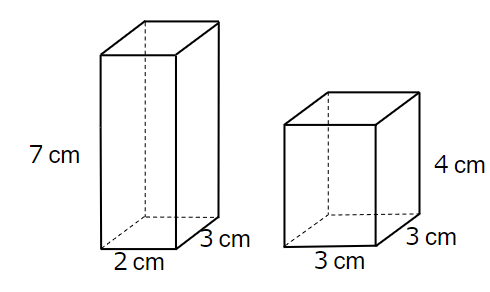
左の四角柱の体積

四角柱の体積は
底面積×高さで求められるから
３×２×７＝４２ｃｍ^３

右の四角柱の体積

四角柱の体積は
底面積×高さで求められるから
３×３×４＝３６ｃｍ^３

合計の体積

左の四角柱の体積＋右の四角柱の体積
＝４２＋３６
＝７８ｃｍ^３

横に切って上下に分ける

同じ立体を、今度は横に切った場合で考えてみるよ。

下の立体を横に切って、体積を求めよう。

知っている形（四角柱）になおすために、赤線のように横に切ってみるよ。

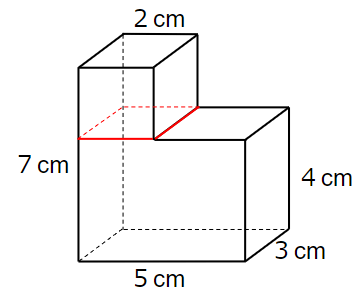
そうすると上下の立体に分けることができるね。
上も下も四角柱だから簡単に体積を求めることができるよね。

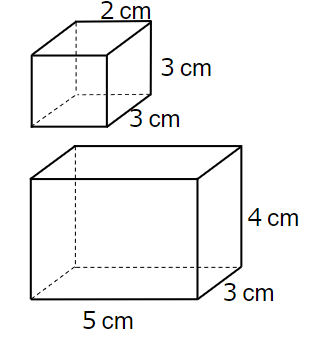
上の四角柱の体積

四角柱の体積は
底面積×高さで求められるから
３×２×３＝１８ｃｍ^３

下の四角柱の体積

四角柱の体積は
底面積×高さで求められるから
３×５×４＝６０ｃｍ^３

合計の体積

上の四角柱の体積＋下の四角柱の体積
＝１８＋６０
＝７８ｃｍ^３

縦に切っても、横に切っても、おなじ結果になるよ。
どちらか、やりやすい方で求めればOKだよ。

複雑な形（凹の形）の立体の体積の求め方

テストでは、階段型よりもさらに複雑な形も登場するよ。
複雑な形の立体の体積を求めるときのポイントは、「角柱の体積をたしたり、ひいたり」して求められないか考えることだよ。

どんな形どうしがくっついたら、その立体の形になるのか、どんな形をひいたら、その立体の形になるのかを考えよう。

下の立体の体積を求めなさい。

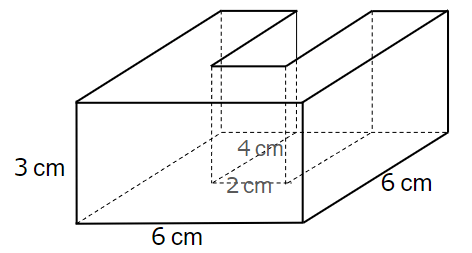
ぱっと見るととても複雑に見えるよね。
でも、この形って、大きな四角柱から小さい四角柱を取りのぞいた形だよね。

なので、求めたい立体は「四角柱から四角柱を引いた体積」ということになるよ。

この立体は、カタカナの「コ」の立体のようなイメージ。
「コ」型や、「凹おう」型と呼ばれたりするよ。

「凹おう」型（コ型）の体積は次のように求められるよ。

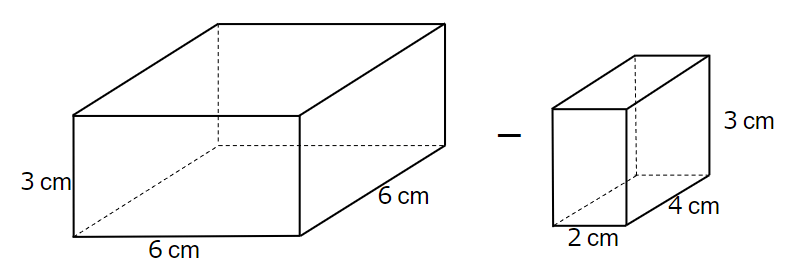
大きい四角柱から、小さい四角柱を引くんだね。
では、まずは大きい四角柱と小さい四角柱の体積をそれぞれ求めていこう。

大きい四角柱の体積

四角柱の体積は
底面積×高さで求められるから
６×６×３＝１０８ｃｍ^３

小さい四角柱の体積

四角柱の体積は
底面積×高さで求められるから
４×２×３＝２４ｃｍ^３

求めたい凹おう型立体の体積

大きい四角柱の体積－小さい四角柱の体積
＝１０８－２４
＝８４ｃｍ^３

複雑な形（バームクーヘンのような形の立体の体積の求め方

下の立体は、半径6cmの円柱の中に、
半径2cmの円柱のくうどうがあります。
高さは4cmです。

体積を求めなさい。

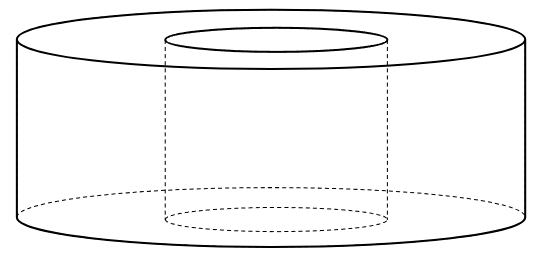
バームクーヘンのような体積は形の立体の体積は
大きな円柱の体積から、小さな円柱の体積を引けば求めることができるね。

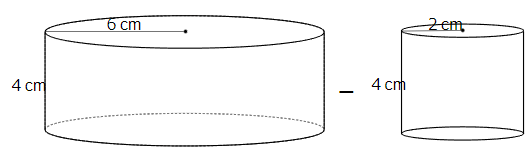
それでは、大きい円柱の体積と、小さい円柱の体積をそれぞれ求めてみよう。

大きい円柱の体積

円柱の体積は
底面積×高さで求められるから
6×6×3.14×4＝452.16cm³

くまごろう

円の面積は、半径×半径×3.14だね。

小さい円柱の体積

円柱の体積は
底面積×高さで求められるから
2×2×3.14×4＝50.24cm³

求めたい立体の体積

大きい円柱の体積－小さい円柱の体積
=452.16－50.24
=401.92cm³

三角柱と四角柱がくっついた形の立体の体積の求め方

次に紹介するのは、三角柱と四角柱がくっついたような形の立体。
今回の問題は、三角柱と四角柱のさかい目が分かれているようになっているけれど、このさかい目がないものもあるよ。

下の立体は三角柱と四角柱がくっついた形の立体です。
体積を求めなさい。

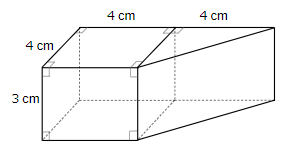
この立体の場合は、三角柱と四角柱に分けて考えればカンタンだね。

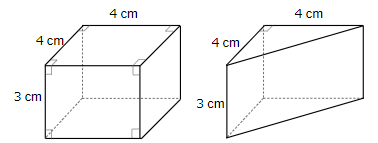
分けることができたら、それぞれ三角柱と四角柱の体積を求めて足したらいいよね。

四角柱の体積

四角柱の体積は
底面積×高さで求められるから
４×４×３＝４８ｃｍ^３

三角柱の体積

三角柱の体積は
底面積×高さで求められるから
４×４÷２×３＝２４ｃｍ^３

求めたい立体の体積

四角柱の体積＋三角柱の体積
＝４８＋２４
＝７２ｃｍ^３

「複雑な形の立体の体積の求め方」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。