「円柱の体積の求め方」公式と問題の解き方をわかりやすく解説
小学校6年生の算数で学習する「円柱の体積の求め方」について、円柱の体積を求める公式と、問題を解く方法をくわしく紹介するよ。
円柱の体積をもとめる円柱を半分にした立体の場合の体積の求め方もくわかりやすく解説しているよ。
円柱の体積の求め方
円柱の体積の求め方を考えてみよう。
「円柱」というのは、「底面が円」の柱状の立体のことだったね。
缶ジュースや、ポテトチップスでよくある筒のような形だね。
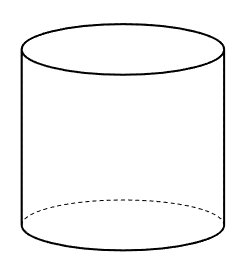
「体積」とは、「その立体にどのくらい水が入るかを表したもの」だとイメージするんだったね。
なので「円柱の体積」は、「円柱に入る水の量」のことだよね。
角柱の体積を求めたときと同じように考えてみよう。
円柱って、底面は「円」だよね。
その円が円柱の高さ分、何枚も何枚も積み重なって、円柱が出来上がるよね。
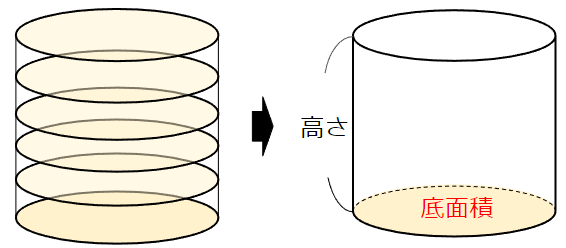
底面の円が高さ分積み重なると円柱ができるから、
体積は「底面積×高さ」で求めることができるんだ。
角柱の体積の求め方と同じだね。
円柱と角柱の体積の求め方の公式を比べてみよう。
円柱と角柱の体積の求め方の公式
- 円柱の体積は「底面積×高さ」
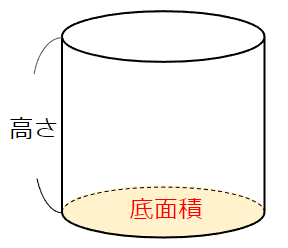
- 角柱の体積は「底面積×高さ」
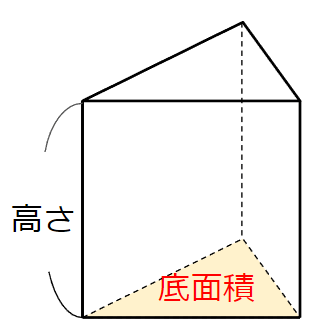
円柱でも角柱でも、体積の求め方は同じだね。
つまり「〇〇柱」の体積は「底面積×高さ」で求めることができるんだね。
円柱の体積の公式
円柱の体積の公式はさっきも紹介したけれど、
底面積×高さで求めることができるよ。
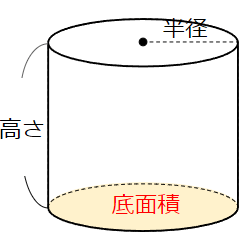
ただ、円柱の底面は「円」だよね。
円の面積は「半径×半径×円周角」で求めることができるから
円柱の体積の公式は次のようになるよ。
円柱の体積の公式
底面積×高さ
=半径×半径×円周率×高さ
半径と高さがわかったら簡単に体積を求めることができるんだ。
では、実際に円柱の体積を求める問題に挑戦してみよう。
円柱の体積の求め方の問題
次の円柱の体積を求めなさい。
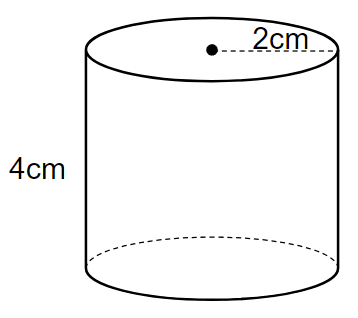
2つの方法で解いてみるよ。
底面積×高さで求める場合
円柱の底面は黄色の場所だよね。
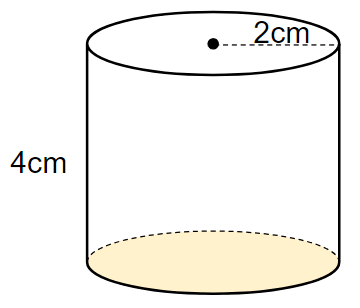
底面だけを切り取ると、次のような半径2cmの円になるよ。
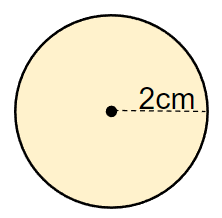
この円の面積は
(半径)×(半径)×(円周率)
=2×2×3.14
=12.56cm2
円柱の底面積が12.56cm2と求まったね。
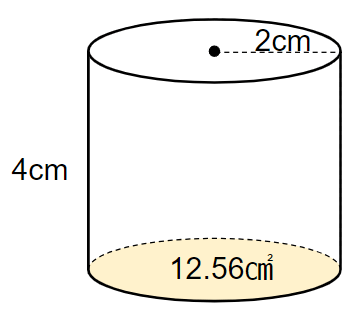
円柱の体積は(底面積)×(高さ)だから
12.56×4=50.24cm3
と求めることができるよ。
半径×半径×円周率×高さで求める場合
半径が2cm、高さが4cmだから、
(半径)×(半径)×(円周率)×(高さ)
=2×2×3.14×4
=50.24cm3
と求めることができるよ。
2つの方法で計算したけれど、同じ答えになることが確認できたね。
自分がやりやすい方法で求められるようにしよう。
円柱を半分にした立体の体積を求める問題
円柱の体積を求める問題では、次のようなタイプも登場するよ。
下の図は円柱を半分にした立体です。この立体の体積を求めなさい。
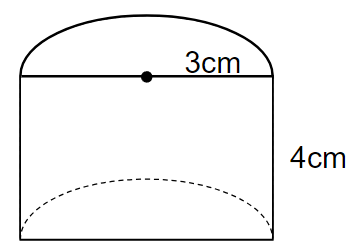
「円柱を半分にした立体」の体積を求める方法は2とおりあるよ。
- 円柱の体積を求めてから半分にする方法
- 半円の面積を求めてから高さをかける方法
順番に紹介していくね。
円柱の体積を求めてから半分にする方法
今回の問題の「円柱を半分にした立体」を、いちど半分にする前の円柱に戻してみよう。
半径3cm、高さ4cmの円柱だから、下の図のようになるね。
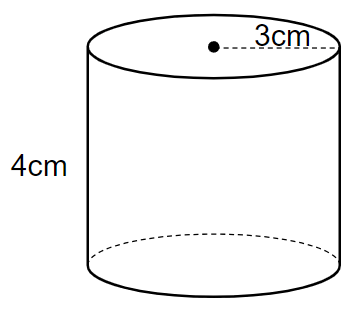
上の円柱の体積は
(半径)×(半径)×(円周率)×(高さ)
=3×3×3.14×4
=113.04cm3
と計算できるよ。
問題の立体は、これを半分にしたものだったね。
なので上の円柱の体積の半分が答えだから
113.04÷2=56.52cm3
になるよ。
半円の面積を求めてから高さをかける方法
円柱に戻さなくても、半分のまま求めることもできるよ。
問題の立体の底面は、黄色の部分の半円だよね。
この半円の面積を求めていこう。
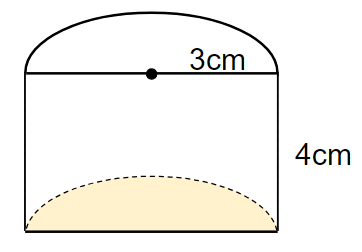
半円のところだけ切り取ると次のようになるよ。
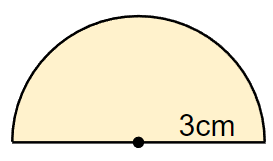
半径3cmの円の面積は
(半径)×(半径)×(円周率)
=3×3×3.14
=28.26cm2
半円だから
28.26÷2=14.13cm2と求めることができたね。
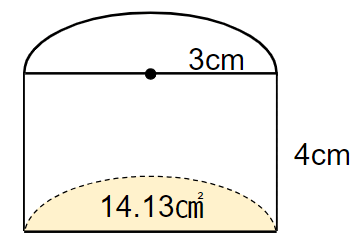
底面積が求まったから、
高さをかけると
14.13×4=56.52cm3
と計算できるね。
円柱の体積の求め方まとめ
円柱の体積の求め方まとめ
- 円柱の体積は底面積×高さで求められる
- 円柱の底面は円だから、底面積は半径×半径×円周率で求められる
- 円柱の体積は半径×半径×円周率×高さでも求められる
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


