「分数の倍」の考え方とやり方は？分数で「倍」をあらわす方法とは

小学校６年生の算数で学習する「分数の倍」について、分数で倍を表す方法、分数の倍をつかった問題の考え方と解き方をわかりやすく解説するよ。

「分数の倍」の考え方とやり方は？ 分数で「倍」をあらわす方法とはのPDF（10枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 「何倍か」を分数であらわしてみよう
• 「分数の倍」の問題
• 「分数の倍」まとめ

「何倍か」を分数であらわしてみよう

苦手な人が多い「何倍か」を求める問題だよ。
ある数が、ある数の何倍かを求めればいいんだよね。

６年生で学習する今回の「分数の倍」だけれど、実は４年生の算数・５年生の算数で今までにやってきた「何倍か」を求める内容に「分数」が登場するだけなんだ。

なので、小学４、５年生の内容がわかっていればそこまで難しい内容ではないよ。
小学４、５年生の復習もしながら「何倍か」を分数であらわしていこう。

式で考える方法

「小学５年生でもやったな」「苦手だな」という声が聞こえてきそうな問題だね。

ある数がある数の何倍かを求めるには、
「比べられる量」÷「もとにする量」＝「〇倍」になるんだったね。

なので、\(\frac{５}{９}\)÷\(\frac{２}{３}\)の式で求めることができるよ。

「比べられる量を、もとにする量で割ったらなんで求まるの？？」という人は、次のように考えてみよう。

さっきの問題を「２をもとにすると、６は何倍か。」のように置き換えてみて。

これだったら、「２をもとにしたら、６は３倍になっている」とわかるね。
そのときの「３倍」というのは、「６÷２」の式で求められるよね。

では、
\(\frac{５}{９}\)÷\(\frac{２}{３}\)
を計算してみよう。

分数のわり算は、掛け算に直して、逆数するから
\(\frac{５}{９}\)÷\(\frac{２}{３}\)
＝\(\frac{５}{９}\)×\(\frac{３}{２}\)

分数の掛け算は、分母同士、分子同士を掛けるから
＝\(\frac{５×３}{９×２}\)

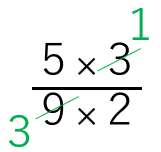
＝\(\frac{５}{６}\)

\(\frac{２}{３}\)をもとにすると、
\(\frac{５}{９}\)は\(\frac{５}{６}\)倍
であることがわかったね。

図で考える方法

さっきと同じ問題を図で考えてみよう。

もとにする量の大きさを１として考えると次のような図になるよ。
今回求めたい「何倍」を「ｘ倍」とおいたよ。

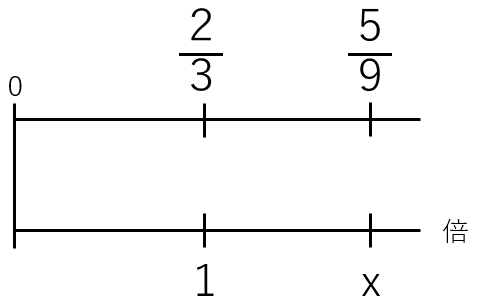
図を見ると、
\(\frac{２}{３}\)をｘ倍したら\(\frac{５}{９}\)になるから
\(\frac{２}{３}\)×ｘ＝\(\frac{５}{９}\)
という式がたてられるね。

ｘを求める式は次のようになるよ。
ｘ＝\(\frac{５}{９}\)÷\(\frac{２}{３}\)

分数のわり算は、掛け算に直して、逆数するから
ｘ＝\(\frac{５}{９}\)÷\(\frac{２}{３}\)
ｘ＝\(\frac{５}{９}\)×\(\frac{３}{２}\)

分数の掛け算は、分母同士、分子同士を掛けるから
ｘ＝\(\frac{５×３}{９×２}\)
＝\(\frac{５}{６}\)

\(\frac{２}{３}\)をもとにすると、\(\frac{５}{９}\)は\(\frac{５}{６}\)倍
であることが図でも説明できたね。

「分数の倍」の問題

それでは実際に「分数の倍」の問題に挑戦してみよう。

式だけで求める方法

もしこれが「色鉛筆の値段は３００円で、消しゴムの値段は、色鉛筆の５倍です。」という問題だったら、
３００×５
で求められるよね。

今回は、５倍ではなく、\(\frac{２}{５}\)倍だから
３００×\(\frac{２}{５}\)
で消しゴムの値段が計算できるよ。

３００×\(\frac{２}{５}\)
＝\(\frac{３００}{１}\)×\(\frac{２}{５}\)　←３００を分数にしたよ。
＝\(\frac{３００×２}{１×５}\)　←約分する

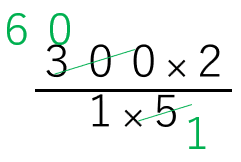
＝１２０

消しゴムの値段は１２０円と求めることができたね。

図を使って求める方法

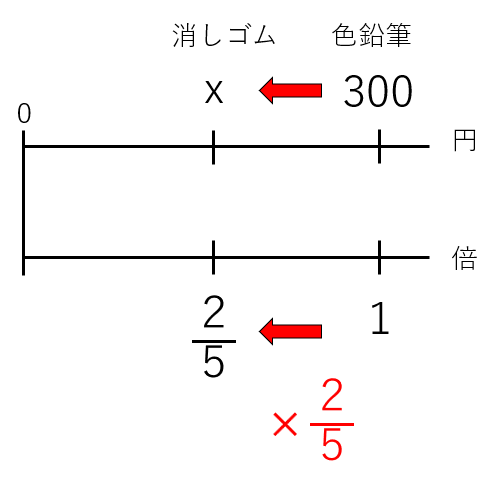
もとにする量の大きさを１として考えると次のような図になるよ。
今回求めたい「消しゴムの値段」を「ｘ円」とおいたよ。

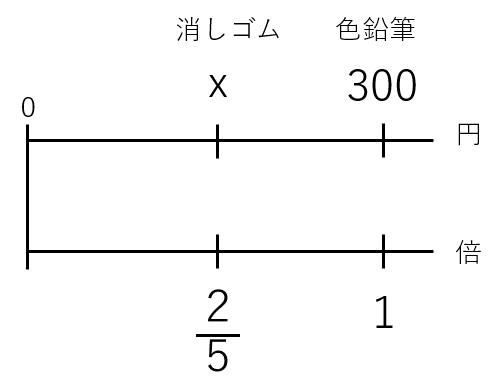
図から式をたててｘを求めていこう

色鉛筆の１を\(\frac{２}{５}\)倍したら、消しゴムになるよね。

ｘ＝３００×\(\frac{２}{５}\)　←さっきと違う方法で計算してみるよ。
ｘ＝\(\frac{３００×２}{５}\)

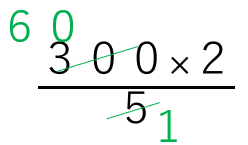
ｘ＝１２０

図を使っても、消しゴムの値段は１２０円と求めることができたね。

式だけで求める方法

もし「色鉛筆の値段は３００円で、色鉛筆の値段は赤ペンの５倍です。」という問題だったら、
赤ペンの値段は
３００÷５
で求められるよね。

今回の問題では、５倍ではなく、\(\frac{５}{３}\)倍だから
３００÷\(\frac{５}{３}\)
で赤ペンの値段が計算できるよ。

分数のわり算は、掛け算に直して、逆数するから
３００÷\(\frac{５}{３}\)
＝３００×\(\frac{３}{５}\)

分数×整数の掛け算は、整数が分子に来て掛けるから
\(\frac{３００×３}{５}\)

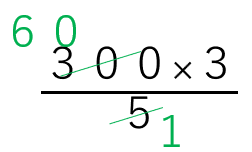
＝１８０

赤ペンの値段は１８０円と求めることができたね。

図を使って求める方法

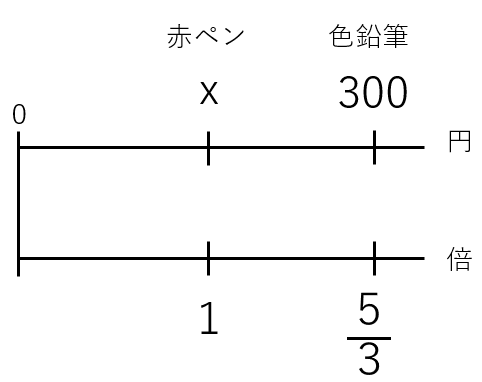
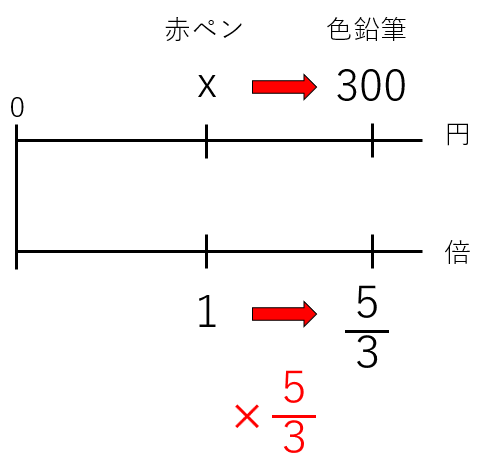
もとにする量の大きさを１として考えると次のような図になるよ。
今回求めたい「赤ペンの値段」を「ｘ円」とおいたよ。

図から式をたててｘを求めていこう

赤ペンの１を\(\frac{５}{３}\)倍したら、色鉛筆になるから次の式が成り立つよ。
ｘ×\(\frac{５}{３}\)＝３００

上の式からｘを求めると
ｘ＝３００÷\(\frac{５}{３}\)　←わり算をかけ算にして逆数にするよ。
ｘ＝３００×\(\frac{３}{５}\)
ｘ＝\(\frac{３００×３}{５}\)

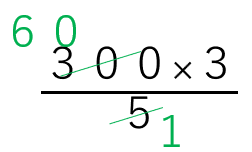
ｘ＝１８０

図を使っても、赤ペンの値段は１８０円と求めることができたね。

「分数の倍」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

1. あ より:

   2024年6月20日 4:14 PM

   わかりやすい

   返信
2. G より:

   2024年7月18日 9:19 AM

   めっちゃわかりやすい

   返信