「ヒストグラム」とは?書き方と見方・度数分布表との関係を解説
小学校6年生の算数で学習する「ヒストグラム」について、ヒストグラム(柱状グラフ)とはどんなグラフか、ヒストグラムの書き方と見方、度数分布表との関係をわかりやすく解説するよ。
度数分布表からヒストグラムを書く問題の考え方も紹介しているよ。
ヒストグラム(柱状グラフ)とは
「ヒストグラム(柱状グラフ)」とは、棒グラフの仲間のグラフだよ。
横軸に「どこからどこまで」という数値の幅をとって、
縦軸に「その数値の幅には何個データがあるか」をとったグラフなんだ。

言葉で説明するよりも、ヒストグラムを書いたほうが理解しやすくなると思うから、実際に問題に挑戦してみよう。
ヒストグラムを書く練習問題①
度数分布表からヒストグラムを書く練習をするよ。
次の度数分布表は1組の生徒20人のハンドボール投げの記録です。
ヒストグラムに表しなさい。
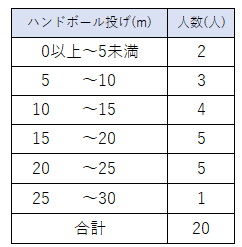
度数分布表を見て、ヒストグラムを書こう。
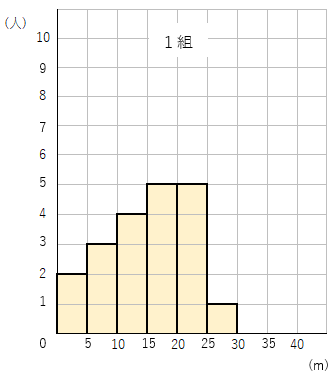
ヒストグラムは棒グラフの仲間だから、次のように棒が並んだように書くよ。
棒がまるで「柱」のようにも見えるので、「柱状グラフ」とも呼ばれるんだね。「状」という漢字には「かたち」という意味があるんだ。
度数分布表の「0~5」の階級の度数は「2」になっているよね。
ということは、ヒストグラムの横軸の「0~5」のところに、縦軸の「2」の高さまでの棒を書くんだよ。
つぎに度数分布表の「5~10」の階級の度数は「3」なので、
ヒストグラムの横軸の「5~10」のところに、縦軸の「3」の高さまでの棒を書くよ。
残りの階級の度数も、同じように書いていけばいいね。
同じ内容を書くなら、どうしてわざわざヒストグラムにするんだろう?
と思うかもしれないね。
度数分布表と、出来上がったヒストグラムを見比べてみよう。


数字だけの度数分布表よりも、ヒストグラムはひと目見ただけで、データの特徴をつかみやすいよね。
ヒストグラムに表すことで全体のちらばりがわかりやすいね。
ヒストグラムを書く練習問題②
次の度数分布表は2組の生徒20人のハンドボール投げの記録です。
ヒストグラムに表しなさい。
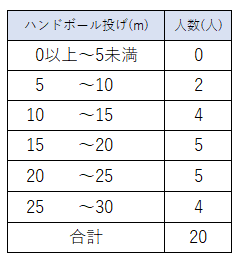
度数分布表を見て、ヒストグラムを書くと次のようになるよ。
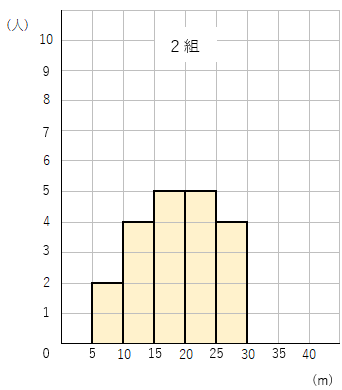
ヒストグラムを比べてみよう
1組と2組のハンドボール投げの記録を比較してみよう。


2組の方が全体的にヒストグラムが右にずれている感じがするね。
このヒストグラムの横軸は、右に行くほど投げた距離が長くなるよね。
ということは、2組の方が遠くまで飛ばしているということだよ。
ヒストグラムに表すことで、2つのデータを比べやすくすることができるんだ。
ヒストグラムから度数分布表を書く練習問題
では、今度は逆にヒストグラムから度数分布表を書く問題に挑戦してみよう。
次のヒストグラムから度数分布表を書きなさい。
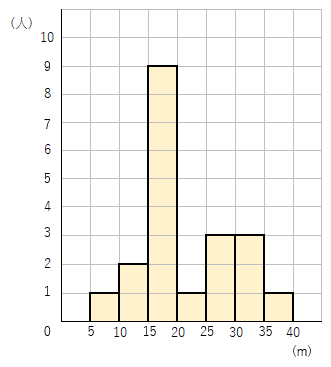
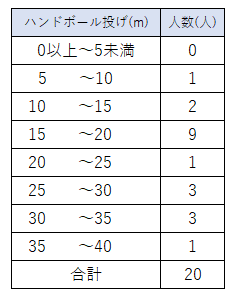
ヒストグラムから度数分布表を作成するには、ヒストグラムを見て、それぞれの数値の幅に、いくつの値があるかを数えて、それを度数分布表にまとめればいいんだ。
- ヒストグラムの数値の幅=度数分布表の「階級」
- ヒストグラムのそれぞれの数値の幅にある値の数=度数分布表の「度数」だよ。
度数分布表は次のようになるよ。
度数分布表を作成して、ヒストグラムに表す練習問題
データをもとに、度数分布表を作成して、さらにヒストグラムに表す問題にも挑戦してみよう。
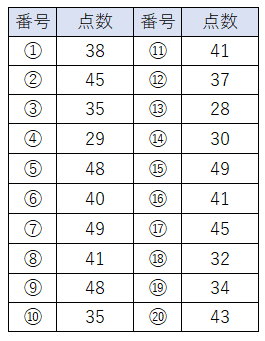
下のデータは生徒20人の漢字テストの結果です。
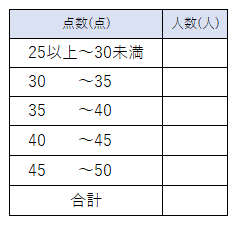
度数分布表に表してから、ヒストグラムを書きなさい。
なんだか大変そうだけれど、ひとつずつ落ち着いてすれば問題ないよ。
まずは、データを度数分布表にまとめよう。
「25点以上~30点未満」の生徒は④の29点の生徒と⑬の28点の生徒の「2人」だね。
ということは、度数分布表の「25以上~30未満」の階級の度数は「2」になるね。
数え忘れがないように注意しながら同じようにデータをまとめていくと、次のようになるよ。
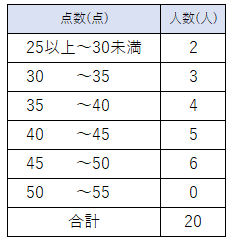
この度数分布表をもとに今度はヒストグラムを書くと次のようになるよ。
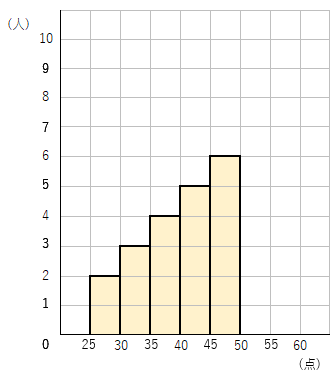
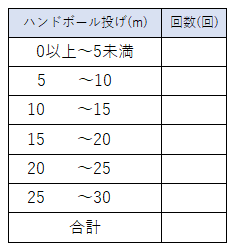
けんたはハンドボール投げを10回やりました。
10回の結果は次の通りです。
度数分布表を作り、ヒストグラムを書きなさい。
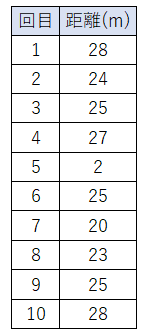
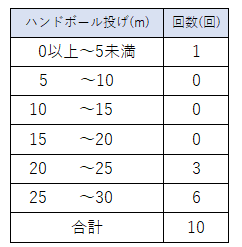
データをもとに度数分布表を書くと次のようになるよ。
度数分布表をもとにヒストグラムを書くと次のようになるよ。
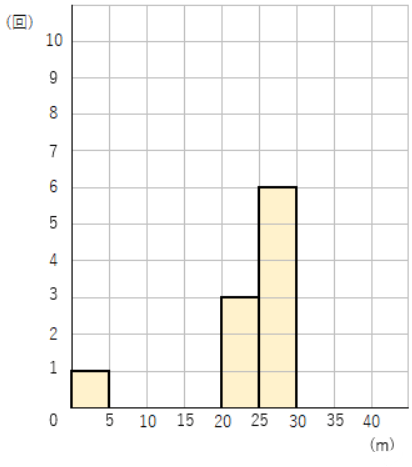
ヒストグラムに表してみると、ぱっと見ても「0~5m」のところの棒だけ他の棒(データ)と離れているよね。
けんたは最高で28mも投げているから、2mしか投げられなかったなんて、なんだかおかしいよね。
「もしかしたら手がすべってしまったのかも?」とか、「投げるときに鳥が飛んできて、投げるのをやめたのかも?」なんて色々な可能性を考えることもできるよね。
このように、ヒストグラムを書くことで「おかしいデータ」が見つけやすくなるよ。
これもデータをヒストグラムに表すことのメリットだね。
ちなみに、この「おかしいデータ」のことを「外れ値」や「異常値」と言ったりするよ。
外れ値や異常値を見つけることができれば、その値を除外したりして、より正確なデータにすることもできるよね。
ヒストグラムから階級の幅を読み取る練習問題
次のヒストグラムは生徒20人のハンドボール投げの結果です。
階級の幅は何mですか。
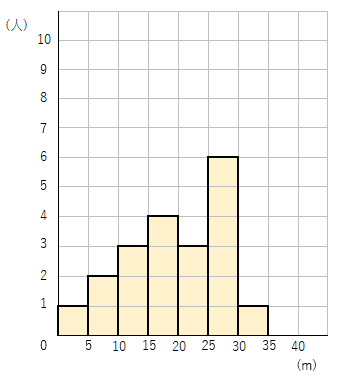
ヒストグラムの横軸の数値の幅=度数分布表の階級の幅だったね。
ヒストグラムの横軸の数値の幅を見ると、「0~5」、「5~10」というように「5m」おきに目盛りがあるので、階級の幅は5mだと読み取れるよ。
「ヒストグラム」まとめ
「ヒストグラム」とは まとめ
- ヒストグラムは横軸に「どこからどこまで」という数値の幅をとり、縦軸に「その数値の幅には何個データがあるか」をとったグラフのこと
- ヒストグラムは度数分布表をもとに書くことができる
- ヒストグラムは「柱状グラフ」ともいう
- ヒストグラムを書くことで、全体のちらばりがわかりやすくなったり、「おかしいデータ」を見つけやすくなる
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


