中央値(メジアン)とは?求め方と代表値のメリットとデメリット
小学校6年生で学習する「中央値(メジアン)」について、中央値の求め方と、「平均値」「最頻値」「中央値」それぞれの特徴とメリットとデメリットをわかりやすく解説するよ。
中央値の求め方についての練習問題にも挑戦しよう。
中央値(メジアン)とは
「中央値」とは、「データを小さい順に並べたときの、真ん中の値のこと」だよ。英語では「メジアン」と言って、つづりは「median」と書くよ。
洋服の「M」サイズって、「ミディアム(medium)」の略で、大中小の「中」のことだよね。
この「ミディアム」と「メジアン」は同じ仲間の言葉なんだ。
medianとmediumで、つづりも似ているよね。
ミディアムのことを思い出せれば、「中央値=メジアン」と覚えやすくなるね。
これまでデータの表し方について、「平均値」や「最頻値」も学習してきたけれど、「中央値」が一番まちがえやすいよ。
だから、テストにはよく出題されるんだ。ここでしっかりおさえておこうね。
5人のテストの点数の中央値を考えよう
それではさっそく「中央値」とはどういうものかくわしく見ていこう。
例えば、下のような5人のテストの点数があったとするよ。
5点・6点・8点・10点・11点
この5人のテストの点数の中央値は「8点」ということになるよ。
だって、5つの点数のデータを点数の小さい順に並べたときに、「8」がちょうど真ん中になるからね。
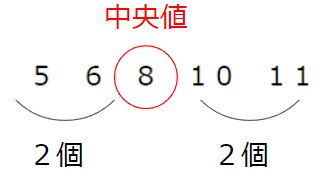
このように、データが奇数個(3、5、7個・・・)のときは、中央値を見つけるのは簡単だね。
6人の点数の中央値を考えよう。
それでは、今度は6人のテストの点数があったとするよ。
5点・6点・8点・9点・10点・11点
さっきと同じように考えたいところだけれど、今度はデータが偶数個なので、小さい順に並べたときに「ちょうど真ん中は8なのか 9 なのかどっち?」となってしまって選べないよね。
そういうときは、
真ん中の2つの数字の平均(2つの数字を足して2で割った数)
が中央値になるんだ。
今回の場合は、真ん中2つの「8」と「9」を足して2で割った「8.5」が中央値になるということだね。
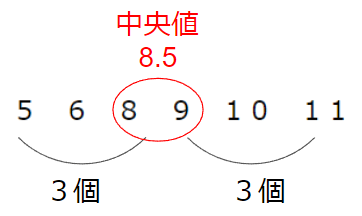
データが偶数個(2、4、6個・・・)のときは、中央値を見つけるのは少し複雑だね。
中央値の求め方
中央値の求め方は、データの数が奇数の場合と偶数の場合で見つけ方が変わってくるよ。
データの数が奇数の場合
データのちょうど真ん中の1つの数がそのまま中央値になる。

データの数が偶数の場合
データの真ん中の2つの数を足して、2で割った数が中央値になる。
中央値を求める問題
8人の漢字テストの点数です。中央値を求めなさい。
4 8 3 9 4 7 6 1 (点)
中央値っていうのは、小さい順に並べたときの真ん中の値だったよね。
だから、まず小さい順に並べることから始めよう。
1 3 4 4 6 7 8 9
こうしたら真ん中の値は4と6だよね。
真ん中の値が2つあるときは、2つをたして2で割ればいいから、
(4+6)÷2=5
中央値が5点になることがわかったね。
9人の漢字テストの点数です。中央値を求めなさい。
4 8 3 9 4 7 6 1 2 (点)
中央値っていうのは、小さい順に並べたときの真ん中の値だったよね。
だから、まず小さい順に並べることから始めよう。
1 2 3 4 5 6 7 8 9
こうしたら真ん中の値は5点だから
中央値は5点になることがわかったね。
代表値とは
代表値とは、データがたくさんあるときに、「そのデータの特徴」を簡単につかむときに使う値のことだよ。
代表値には、「平均値」「最頻値」「中央値」の3つがあるんだ。

なんで「代表」という名前がついているのか、そしてどうして代表値を求める必要があるのかを説明するね。
データの特徴を調べたり伝えたりするときには、平均値や最頻値や中央値のうち、1つの値で代表させて、それらを比較することがあるんだ。
たとえば、学校の定期テストを生徒200人が受けたとして、「15点」の子がいたり、「90点」の子がいたりと、データをひとつひとつ見ているだけでは特徴がつかみづらいよね。
「そのテストって、難しかったの?」と聞かれた時に、「15点しか取れなかった子がいる」と思えば難しいように思うけれど、「90点」の子もいると考えると、もしかしたら簡単だったのかもしれないしね。
そんなとき、「平均点」を求めて、それが「40点」だったと分かったらどうだろう?
「けっこう難しかったんだね。」と考えることができるよね。
そして、「90点を取ったなんて、すごいね!」とも思えるよね。
テストAとテストBがあったときに、テストAの平均点は「30点」で、テストBの平均点は「80点」だったら、テストAの方が難しいテストなんだな、と判断することができるよね。
このように、データの「代表値」を求めることで、データの特徴をつかんだり、データを比較することができるんだ。
では、なぜ「平均値」「最頻値」「中央値」の3つも代表値の種類があるんだろう。
それは、それぞれ得意なことと苦手なこと(メリットとデメリット)があるからだよ。
「平均値」「最頻値」「中央値」それぞれのメリットとデメリット
まずは、「平均値」「最頻値」「中央値」とはそれぞれどういうものか、もういちど確認してみよう。
代表値とは
- 平均値:平均と同じで、合計を個数(データの数)で割った値
(データ全体を平らにしたときの値) - 最頻値:もっとも多く出てくる値
- 中央値:データを小さい順に並べたときの真ん中の値
| 代表値 | 計算方法 | メリット | デメリット |
|---|---|---|---|
| 平均値 | 合計÷個数 | 全てのデータをもとに算出できる | 外れ値の影響を受けやすい |
| 最頻値 | もっとも多く出てくる値を求める (度数分布表の場合、もっとも度数が大きい階級値になる) | 外れ値の影響を受けにくい | ・複数のデータが最頻値になる場合がある ・データの数が少ないと最頻値を求めることができない(すべてが「1つ」しか出ないなど) |
| 中央値 | データを大きさ順(小さい順)に並べたときに真ん中にある値(偶数個のデータの場合は、真ん中2つの数の合計÷2) | 外れ値の影響を受けにくい | 外れ値の影響を受けにくい反面、全てのデータを反映しているとはいえない |
平均値のメリットとデメリット
平均値のメリットは、なんといっても「全てのデータをもとにしている」こと。
たとえば、あるクラスのテストの点数について、ほとんどみんなが10点前後しかとれなかった中、A君だけが100点をとれた場合を考えてみよう。
平均点をもとめるときに、「A君の100点は無かったことにしよう」なんてしないよね。
ちゃんと全てのデータをもとに算出するから、公平だね。
ではデメリットは何かと言うと、外れ値に影響を受けやすいこと。
外れ値とは、「極端に外れている値」のことだったね。
たとえば、ほとんどみんなが10点前後の中、A君の100点って、ちょっと外れているよね。
A君の100点を含めて平均値を求めるので、平均値(平均点)は高めになるよね。
平均点を見ただけでは「みんな10点しか取れないくらい難しいテストだったんだ」ということには気が付けないね。
最頻値のメリットとデメリット
平均値にくらべて、最頻値は外れ値の影響を受けにくいよ。
たとえば、さっきのテストの点数の例で考えると、20人の生徒がテストを受けていて、そのうち「10点」をとった人がいちばん多いとするよね。
そうすると、最頻値の「10点」がそのデータの代表値になるね。
さっきのように100点のような外れ値があっても、外れ値の数が少ない限り問題はないよね(そもそも、数が少ないから外れ値なんだよね)。
そんな最頻値の弱点は、「あるていどデータの数がないと、最頻値が求められない」こと。
なぜなら、データの数がじゅうぶんにないと、「いちばん多い値」を探すのに、「どのデータも1つずつしかない」なんてこともあるんだ。
そのほかにも、「10点が5人、20点も5人」のように、多い数の値が複数になってしまって、1つに決めることができないなんてこともあるよ。
中央値のメリットとデメリット
中央値も、外れ値の影響を受けにくいよ。
なぜなら、外れ値って、データを大きさ順に並べた場合、いちばん小さいか大きいかのどちらかで、「外側」にあるよね。
だから、「真ん中」を選ぶ中央値なら、外れ値が影響することはほぼ無いんだ。
でもその分、外れ値がほとんど「無かったこと」のようになってしまうのがデメリットだよ。
「平均値」「最頻値」「中央値」それぞれの特徴とメリット・デメリットをわかったうえで、「そのデータの特徴をあらわすのには、どの代表値を使うのがよいかな?」と考える必用があるね。
「中央値(メジアン)」と代表値まとめ
- 中央値とはデータを小さい順に並べたときの真ん中の値
- データの数が奇数の場合の中央値は

- データの数が偶数の場合の中央値は

- 中央値・平均値・最頻値をまとめて代表値という
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



すごくためになりました!