比の値とは?分数・小数の比の値の求め方も簡単に解説(練習問題)
小学校6年生の算数で学習する「比」について、「比」とはなにか、「比の値」とはなにか、比の値の求め方をわかりやすく簡単に解説しているよ。
比が分数だった場合の、比の値の求め方、比が小数だった場合の比の値の求め方も紹介。練習問題で、比の値の求め方をマスターしよう!
割合の表し方「比」とは?
「比」っていうのは、「比べる」という字からわかるように
2つ以上の数字を比べることだよ。
例えば、男子20人、女子10人のクラスがあったとしよう。
比は次のようになるよ。
男子20と女子10。
当たり前のことだよね。
ただ、気を付けてほしいことは
「比」と「比例」は全く違うものだよ。
「比」は、どちらがのほうが多いかとか、もう片方にくらべて何倍か、というように2つ以上の数字を比べるのに便利なんだ。
※ちなみに、「比例」は、片方が倍になると、もう片方も倍になるなどの関係にある2つの数字のことだったね。
比をあらわす記号「:」
2つの数字を比べるのに、いちいち「男子20と女子10」と書いていたらめんどうだよね。
そこで登場するのが、比をあらわす記号「:」だよ。
「:」の読み方は「対(たい)」。
さっきの「男子20と女子10」だったら、
20:10(20対10)とあらわすことができるんだ。
2つのチームが戦うときに、「青チーム 対(たい) 赤チーム」なんていうよね。
「比」も、2つの数字を比べるので、「対(たい)」と読むとイメージするといいね。
なんとなく「比」についてわかってきたね。
できるだけ簡単な比であらわす
「比」は、2つの数字を比べることだったよね。
比べるときは、できるだけ「わかりやすい」ほうがいいよね。
だから、「比」を「できるだけ簡単な比であらわす」ことが必要になったりするんだ。
さっきの「男子20と女子10」をできるだけ簡単な比にしてみよう。
男子20と女子10を、それぞれ「10」で割れば、男子が2で女子は1になるね。
だから
20:10=2:1
とあらわすことができるんだ。
これを「できるだけ簡単な比であらわす」というよ。
できるだけ簡単な比にするには、2つの数字の最大公約数で割るといいよ。
最大公約数は、小学校5年生で習ったね。
最大公約数とは、2つ以上の数字があったとき、それらすべてを割り切ることができる数字のうち、最も大きい数のことだね。
できるだけ簡単な比であらわす練習
①6:2 (2でわって)
→3:1
②10:4 (2でわって)
→5:2
③30:24 (6でわって)
→5:4
比であらわすことのよさ
こうやって比であらわすと、
2つの数の大きさの違いがわかって
比べやすくなるよね。
たとえば、次の2つだったらどちらの方がわかりやすいかな?
「男性が62,110,753人、女性が65,379,740人」
「男性:女性の割合は19:20」
ぱっと見て、
「男性:女性の割合は19:20」
の方が2つの数の大きさの違いがわかりやすいよね。
「男性19人に対して、女性が20人いる感じね」
となるよね。
比の値とは?比の値の求め方
比には重要な性質があるんだ。
それが「比の値」だよ。
比の値っていうのは、比を分数に置き換えたもののこと。
「どういうこと?」と思うかもしれないけど、
まずは、求め方を覚えてしまおう。
比の値の求め方
教科書では、比の値の求め方が次のように書かれているよ。
比の値の求め方
a:bの比の値は\(\frac{a}{b}\)とあらわすことができる。
ちょっとピンとこないかもしれないね。
簡単に言ってしまうと、比から「比の値」を求めるには「:」の部分を「÷」と書き換えてあげればいいよ。
例えば、
3:4という比だったら
比の値は
3÷4=\(\frac{3}{4}\)
とあらわすことができるよ。
同じように
5:7という比だったら
比の値は
5÷7=\(\frac{5}{7}\)
となるよ。
ちなみに、aがbで割り切れる数字の場合は、比の値は分数にはならずに整数や小数になるよ。
「a:bの比の値は\(\frac{a}{b}\)とあらわすことができる。」
というのは、「aをbで割った値が、比の値である」ということを伝えたいだけで、「分数にしなさい」と言っているわけではないので注意してね。
比の値とは
比の値の意味について考えてみよう。
8:4なら比の値は
8÷4=\(\frac{8}{4}\)=2になるよね。
式を言葉に言い換えると、
「8は4の何倍になっているかを求めると「2倍」である。」
となるよね。
「比」は、もともと「2つの数を比べる」ことだったよね。
だから、「比べた結果、どちらがどのくらい大きいのか?」ということを考えないと意味がないよね。
その「どちらがどのくらい大きいか」を考えて求めるのが、「比の値」なんだ。
だから、式の値というのは、
「2つの数を比べたとき、片方はもう片方の何倍になっていますか?」
ということをあらわす値だと思っておけばOK。
a:bだったら、式の値は\(\frac{a}{b}\)だよね。
これは、aはbの何倍になっているかを表しているよ。
式の値が「2」だったら、aはbの2倍だし、式の値が「4」だったら、aはbの4倍ということ。
式の値が大きければ大きいほど、aの方がbよりも大きくなるイメージだね。
分数の比の値の求め方
これまでは、「整数:整数」の例を紹介したけれど、比には分数が混ざることもあるよ。
では、分数の比の値の求め方を確認しよう。
例えば、次のような比の値を求めてみよう。
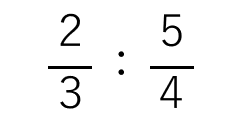
比を比の値(分数)に直すには
「:」の部分を「÷」と書き換えてあげればいいから
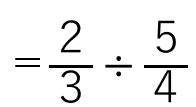
分数÷分数の計算は、
わり算をかけ算にして、逆数にしたらよかったから
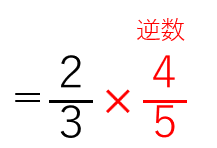
分数×分数の計算は、
分母同士、分子同士を掛けたらよかったから
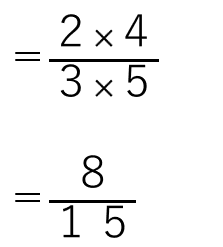
と求めることができるよ。
小数の比の値の求め方
比には、整数と分数の他にも、小数が使われていることもあるんだ。
では、今度は小数の比の値の求め方を確認しよう。
小数の比の値は、
- 小数のまま計算する方法と
- 分数に直してから計算する方法
があるよ。
小数のまま計算する方法
例えば、次のような比の値を求めてみよう。
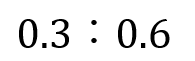
比を比の値(分数)に直すには
「:」の部分を「÷」と書き換えてあげればいいから
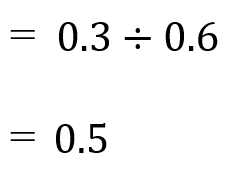
と求められるよ。
分数に直して計算する方法
0.3とか0.6を分数にすると、
\(\frac{3}{10}\)と\(\frac{6}{10}\)だよね。
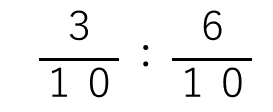
じゃあ、この比の「比の値」を求めよう。
「:」の部分を「÷」と書き換えて計算していくと次のようになるよ。

\(\frac{1}{2}\)は0.5のことだから
小数のまま計算する方法と同じ答えになるね。
小数のまま計算する方法と分数に直す方法を紹介したけれど、「どちらで計算するか」は、テストなどで、「小数で答えなさい」とか「分数で答えなさい」ととくべつな指示がなければ、どちらかやりやすい方で大丈夫。
比の値を求める練習問題
それでは、比の値を求める練習問題をやっていこう。
比の値を求める基本問題
次の比の「比の値」を求めなさい。
5:4
比を比の値(分数)に直すには
「:」の部分を「÷」と書き換えてあげればいいから
比の値は
5÷4=\(\frac{5}{4}\)
と求められるよ。
分数の比の値を求める問題
次の比の「比の値」を求めなさい。
\(\frac{3}{5}\):\(\frac{3}{2}\)
比を比の値(分数)に直すには
「:」の部分を「÷」と書き換えてあげればいいから
比の値は
\(\frac{3}{5}\)÷\(\frac{3}{2}\)
分数÷分数の計算は、
わり算をかけ算にして逆数にしたらいいから
=\(\frac{3}{5}\)×\(\frac{2}{3}\)
=\(\frac{3×2}{5×3}\)
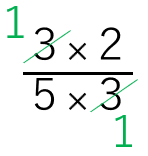
=\(\frac{2}{5}\)
と求められるよ。
小数の比の値を求める問題
次の比の「比の値」を求めなさい。
0.6:1.5
比を比の値(分数)に直すには
「:」の部分を「÷」と書き換えてあげればいいから
比の値は
0.6÷1.5=0.4
と求められるよ。
比の値の計算機
大きい数や複雑な数の比を、簡単にすることができる計算機サイトを紹介するよ。
「算数の電卓」では、大きな数の比や、小数の比を入力することで、簡単な比に直して表示してくれるよ。
「比」「比の値」まとめ
- 「比」とは、2つの数字を比べること。
- 「比の記号」は、「:」で「対(たい)」と読む。
- a:bの比の値は\(\frac{a}{b}\)とあらわすことができる。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


