「分数割る分数」の計算・やり方をわかりやすく説明（練習問題）

小学校６年生の算数で学習する「分数割る分数」の計算のやり方を、わかりやすく解説するよ。

分数割る分数は、割る数の分数を逆数にして掛ける方法を使うと簡単に求めることが出来るよ。
どうして逆数を使うのか、掛け算と割り算が混ざっている場合はどうするのかなど、くわしく紹介しているよ。

「分数割る分数」の計算やり方をわかりやすく説明（練習問題）のPDF（11枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

「分数割る分数」の計算・やり方

分数÷分数の計算のやり方を考えてみよう

次の分数÷分数のやり方を考えよう。

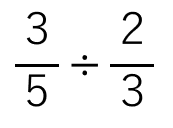
今まで、「分数×整数」と「分数÷整数」の計算はやってきたよね。
だから、「分数×整数」「分数÷整数」の形に無理やり変えちゃうよ。

割られる数である\(\frac{３}{５}\)と、割る数である\(\frac{２}{３}\)それぞれに３をかけよう。
そうすると、今まで学習した「分数÷整数」の形になるんだ。

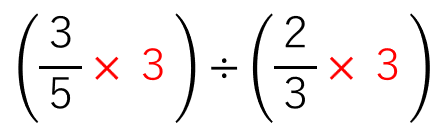
割られる数と割る数それぞれに「３」をかけても答えは変らない理由

割り算は、「割られる数」は、「割る数」の何倍にあたるか、という考え方ができるよね。

たとえば、次の計算で考えてみよう。

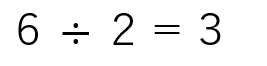
６÷２＝３という関係は、「６」は「２」の３倍、というふうに表すことができるよね。
ということは、割られる数と、割る数それぞれに同じ数をかけてあげても、この関係はくずれないんだ。

実際に試してみよう。

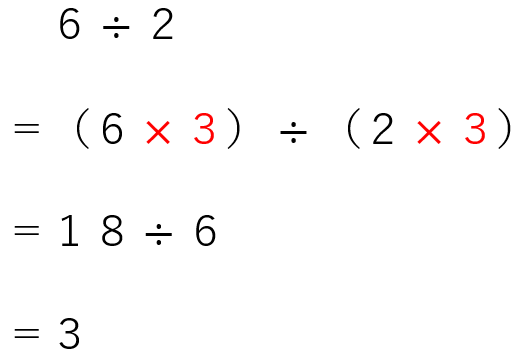
割られる数の６と、割る数の２に、それぞれ「３」を掛けても答えは変らないよね。

じゃあ、本題に戻ろう。
\(\frac{３}{５}\)と\(\frac{２}{３}\)に３をかけると、次のようになるね。

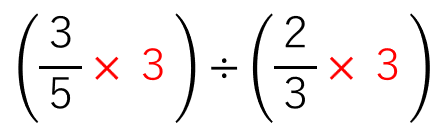
（　）の中の、分数×整数の計算は、整数が分子に来て掛ければよかったから

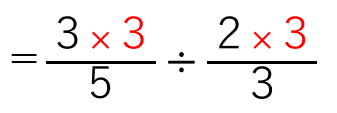
約分すると

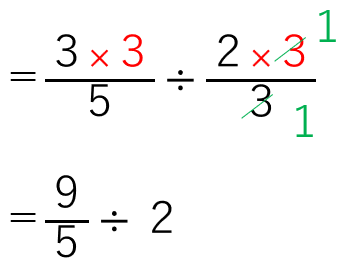
今まで学習した「分数÷整数」の形になったね。
ここまでできたら、あともう少し。
分数÷整数の計算は、整数が分母に来て掛ければよかったから

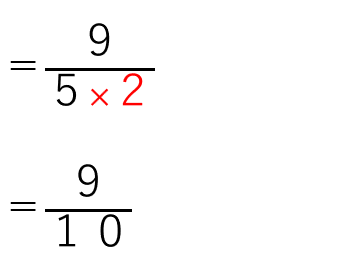
と求めることができたね。

もう一度、式と答えを確認すると次のようになるよ。

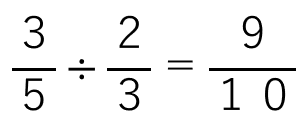
他の問題にも同じやり方で挑戦してみよう。

次の分数÷分数のやり方を考えよう。

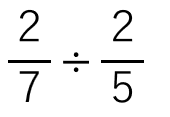
\(\frac{２}{７}\)と\(\frac{２}{５}\)に５をかけよう。
そうすると、今まで学習した「分数÷整数」の形になるんだ。

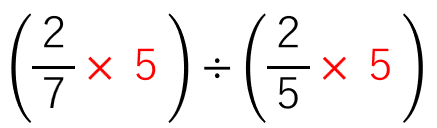
分数×整数の計算は、整数が分子に来て掛ければよかったから

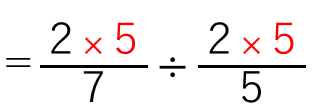
約分すると

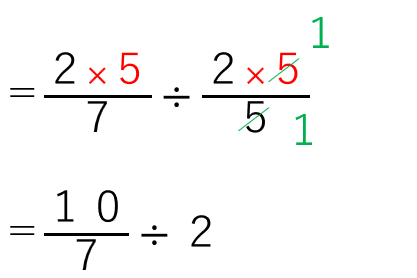
今まで学習した「分数÷整数」の形になったね。
ここまでできたら、あともう少し。
分数÷整数の計算は、整数が分母に来て掛ければよかったから

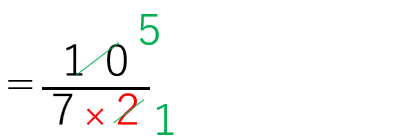
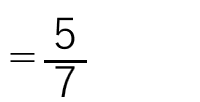
と求めることができたね。

もう一度、式と答えを確認すると次のようになるよ。

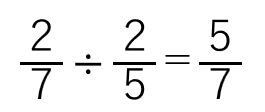
「分数割る分数」を逆数を使って解いてみよう

分数÷分数の計算を２問やったね。
「なんか複雑だな」「めんどくさいな」と思った人もいるよね。
ただ、逆数を使った「分数割る分数」のやり方を知っていれば、簡単に計算することができるんだ。

さっきの計算からわかることは何だろうか？

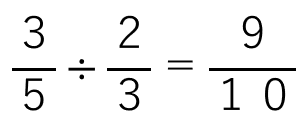
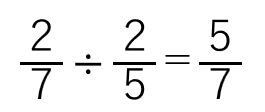
÷を×にして、後ろの分数を逆数にしてみると、あることに気がつくんじゃないかな？

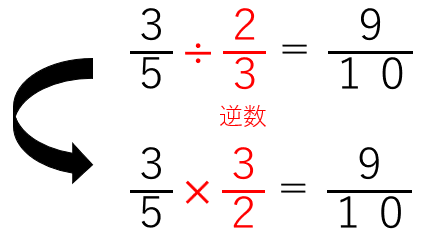
÷を×にして後ろの分数を逆数にすると、
分母同士、分子同士掛けたものが答えになっているね。
・分母５×２＝１０
・分子３×３＝９

÷を×にして後ろの分数を逆数にすると、
分母同士、分子同士掛けたものが答えになっているね。
・分母７×２＝１４
・分子２×５＝１０
→\(\frac{１０}{１４}\)を約分して\(\frac{５}{７}\)

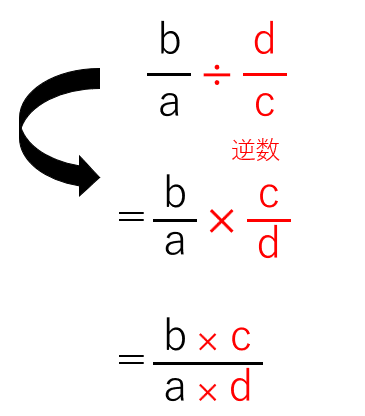
分数÷分数のやりかた（逆数を使う方法）

分数で割る計算は、分数を逆数にして掛ける

分数割る分数の問題

それでは、実際に分数÷分数の練習問題に挑戦してみよう。

\(\frac{７}{９}\)÷\(\frac{３}{２}\)を計算しなさい。

分数でわる計算は、分数を逆数にして掛ければいいから
\(\frac{７}{９}\)÷\(\frac{３}{２}\)
＝\(\frac{７}{９}\)×\(\frac{２}{３}\)

分数×分数の計算は、分母同士、分子同士を掛ければいいから、
＝\(\frac{７}{９}\)×\(\frac{２}{３}\)
＝\(\frac{７×２}{９×３}\)
＝\(\frac{１４}{２７}\)

※答えが求まったら、約分ができないかどうか確認をしておこう。

\(\frac{１}{３}\)÷\(\frac{１}{２}\)を計算しなさい。

分数でわる計算は、分数を逆数にして掛ければいいから
\(\frac{１}{３}\)÷\(\frac{１}{２}\)
＝\(\frac{１}{３}\)×\(\frac{２}{１}\)

分数×分数の計算は、分母同士、分子同士を掛ければいいから、
＝\(\frac{１}{３}\)×\(\frac{２}{１}\)
＝\(\frac{１×２}{３×１}\)
＝\(\frac{２}{３}\)

※答えが求まったら、約分ができないかどうか確認をしておこう。

\(\frac{４}{３}\)÷\(\frac{２}{５}\)を計算しなさい。

分数でわる計算は、分数を逆数にして掛ければいいから
\(\frac{４}{３}\)÷\(\frac{２}{５}\)
＝\(\frac{４}{３}\)×\(\frac{５}{２}\)

分数×分数の計算は、分母同士、分子同士を掛ければいいから、
＝\(\frac{４}{３}\)×\(\frac{５}{２}\)
＝\(\frac{４×５}{３×２}\)

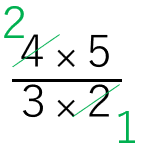
＝\(\frac{１０}{３}\)

\(\frac{４}{３}\)÷７を計算しなさい。

７は分数にしたら、\(\frac{７}{１}\)だよね。

分数でわる計算は、分数を逆数にして掛ければいいから
\(\frac{４}{３}\)÷\(\frac{７}{１}\)
＝\(\frac{４}{３}\)×\(\frac{１}{７}\)

分数×分数の計算は、分母同士、分子同士を掛ければいいから、
＝\(\frac{４}{３}\)×\(\frac{１}{７}\)
＝\(\frac{４×１}{３×７}\)
＝\(\frac{４}{２１}\)

\(\frac{４}{３}\)÷\(\frac{２}{３}\)×\(\frac{５}{２}\)を計算しなさい。

今までは２つのわり算だったけど、
今度は３つで、掛け算とわり算が混ざっているね。

まず、分数でわる計算は、分数を逆数にして掛ければいいから
\(\frac{４}{３}\)÷\(\frac{２}{３}\)×\(\frac{５}{２}\)
＝\(\frac{４}{３}\)×\(\frac{３}{２}\)×\(\frac{５}{２}\)

分数×分数×分数の計算は、分母同士、分子同士を掛ければいいから、
＝\(\frac{４}{３}\)×\(\frac{３}{２}\)×\(\frac{５}{２}\)
＝\(\frac{４×３×５}{３×２×２}\)

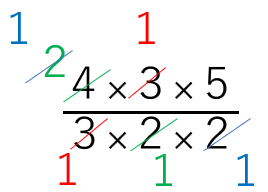
＝５

「分数割る分数」まとめ

分数を分数で割る計算のポイントは次の通りだよ。

分数÷分数

分数でわる計算は、分数を逆数にして掛ける

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。