「縮図の利用」縮図を使う木の高さの求め方は?問題の解き方を解説
小学校6年生の算数で学習する「縮図の利用」について、縮図を使って木の高さを求める方法や、建物の高さ、橋の長さなどの問題の解き方をわかりやすく解説するよ。
縮図を使って木の高さを求める問題
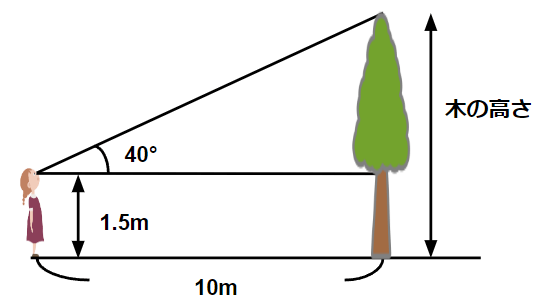
下の図は、花子さんが木から10m離れたところに立って、
木のてっぺんを見上げている様子を表しています。
木の高さは何mですか。
実際に木の高さを測るのは大変だよね。
いちいち、「はしご」を持ってくるのもめんどうだしね。
そんなとき「縮図」を使えば簡単に高さを求めることができるんだ。
STEP1 図を簡単に書こう。
上の図をもっと簡単に書いてみると次のようになるよね。
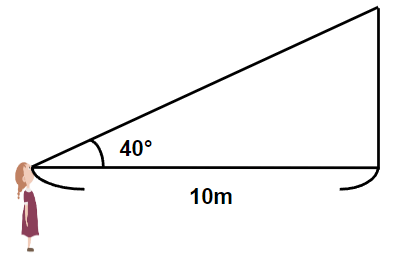
(今回の計算で大事なところは目線より上のところだから、下の部分と木は消しているよ。)
STEP2 縮図を書くために縮尺を決めよう。
「縮図」とは、実物よりも大きさを小さくした図のことだったよね。
そして「縮尺」とは、どのくらい小さくするかを表すことばだったね。
※「縮尺」についてよくわからなかったら、縮尺について解説しているページを確認しよう。
どのくらい小さく書くかはノートの大きさ次第って感じかな。
例えば、\(\frac{1}{10}\)の縮図を書くとすると、
人と木の距離は10m×\(\frac{1}{10}\)=1mになるね。
1mはノートに書くことができないから、
もっと縮小する必要があるよね。
なので今回は\(\frac{1}{100}\)の縮図を書くことにしよう。
STEP3 縮図を書こう
縮図を書くときには、定規と分度器が必要になるから準備しておこう。
10mを\(\frac{1}{100}\)にすると、10m×\(\frac{1}{100}\)=0.1m。
0.1mとは10cmのことだから、
三角形の底辺は10cmになるよ。
縮図の書き方
①10cmの底辺を書く
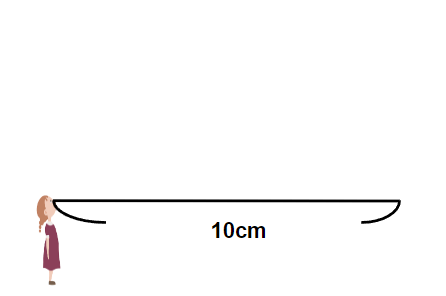
②分度器で40°を測る
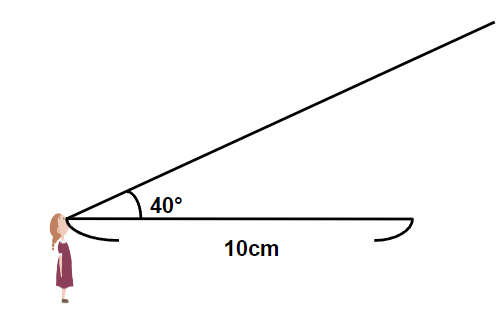
拡大図・縮図では、角度は変らないから、元の図形と同じ40°だよ。
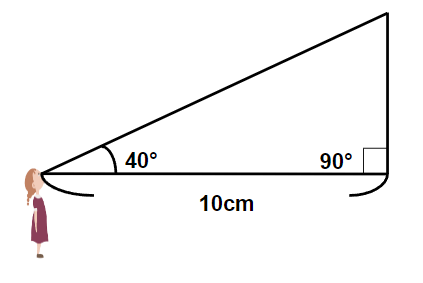
③分度器で90°を測る
木は地面に90°で生えているから90°を分度器で測るよ。
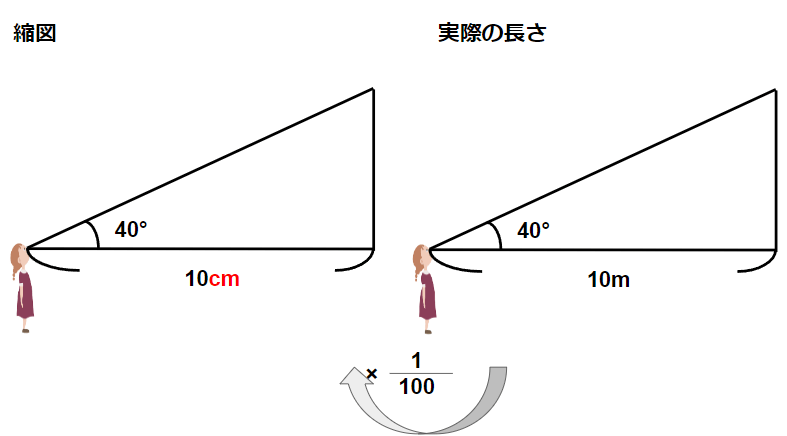
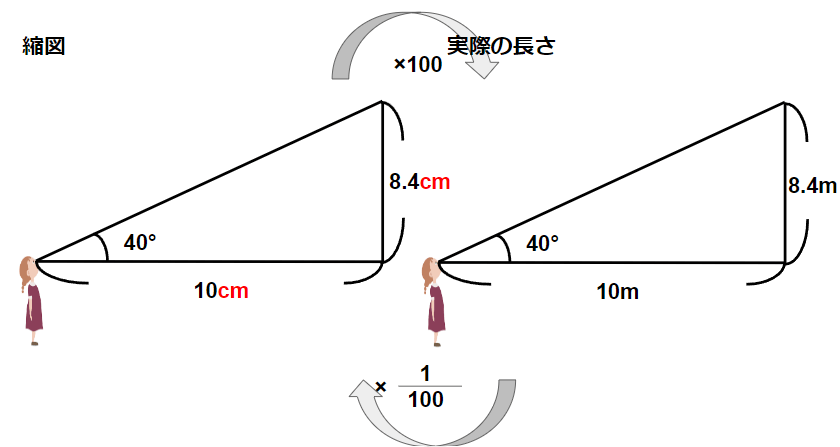
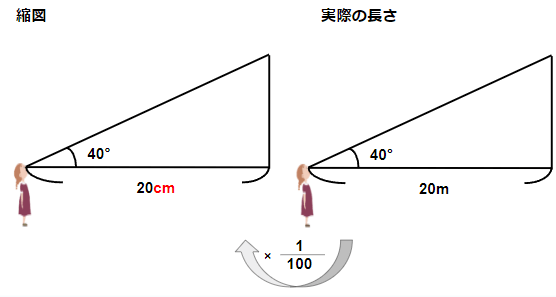
縮図と実際の長さの図を並べてみると次のようになるよ。
単位が違うことに注意しよう。
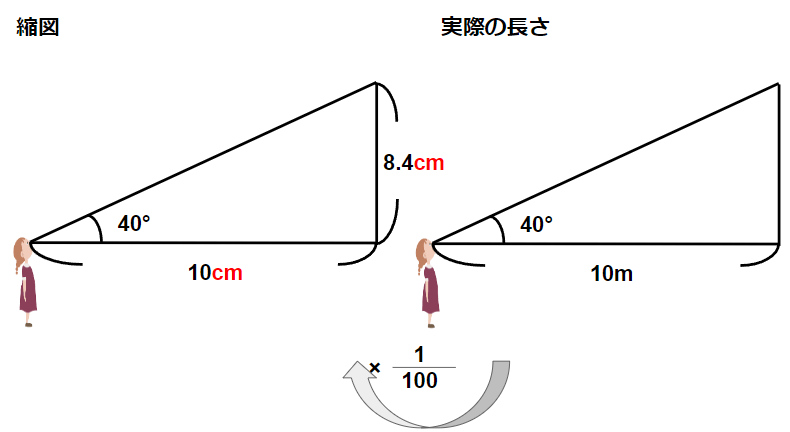
STEP4 縮図の高さを定規で測ってみよう
縮図の三角形の高さを定規で測ると
8.4.cmになるよ。
STEP5 実際の三角形の高さを求めよう
縮尺は\(\frac{1}{100}\)だったよね。
実際の長さを\(\frac{1}{100}\)したら縮図の長さになるということだね。
今度は縮図の長さをもとに、実際の長さをしりたいので、これを反対に考えてみよう。
縮図の長さを100倍したら実際の長さになるから、
縮図の8.4cmは、実際の8.4×100=8400cmということ。
8400cmというのは8.4mのことだから、
実際の高さは8.4mと求めることができるよ。
STEP6 木の高さを求めよう
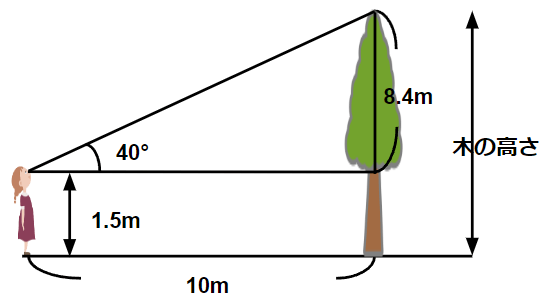
最初の図に、今回わかった8.4mを書き入れてみよう。
ここで注意。
答えを「木の高さは8.4m」としてしまったら間違いだよ。
上の図をみてわかるとおり、さっき求めた高さに人の目線の高さを足さないといけないよね。
だから8.4に1.5を足すよ。
8.4+1.5=9.9
木の高さは9.9mと求めることができるね。
縮図を使って建物の高さを求める問題
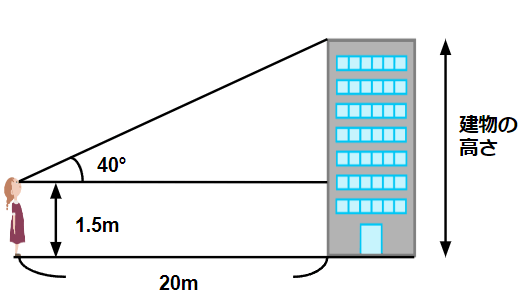
下の図は、花子さんがある建物から20m離れたところに立って、
建物の上のはしを見上げている様子を表しています。
建物の高さは何mですか。
さっきの「木の高さを求める問題」と解き方は全く同じ。
だから復習しながら答えを求めてみよう。
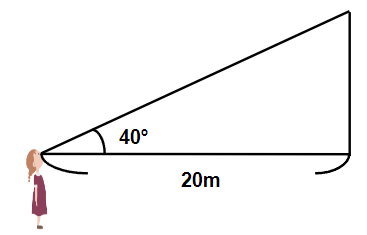
STEP1 図を簡単に書こう。
上の図をもっと簡単に書いてみると次のようになるよね。
※今回の計算でも大事なところは目線より上のところだから、下の部分と建物は消しているよ。
STEP2 縮図を書くために縮尺を決めよう。
縮図は実物よりも大きさを小さくした図のことだったよね。
どのくらい小さく書くかはノートの大きさ次第。
例えば、\(\frac{1}{10}\)の縮図を書くとすると、
人と建物の距離は20m×\(\frac{1}{10}\)=2mになるね。
2mはノートに書くことができないから、
もっと縮小する必要があるよね。
今回は\(\frac{1}{100}\)の縮図を書くことにしよう。
STEP3 縮図を書こう
20mを\(\frac{1}{100}\)にすると、20m×\(\frac{1}{100}\)=0.2m。
0.2mとは20cmのことだから、
三角形の底辺は20cmになるよ。
STEP4 縮図の高さを定規で測ってみよう
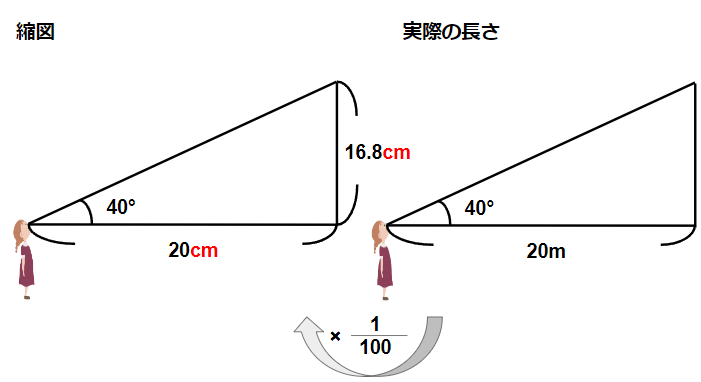
縮図の三角形の高さを定規で測ると
16.8cmになるよ。
STEP5 実際の三角形の高さを求めよう
縮尺は\(\frac{1}{100}\)だったよね。
実際の長さを\(\frac{1}{100}\)したら縮図の長さになるということだね。
反対に考えよう。
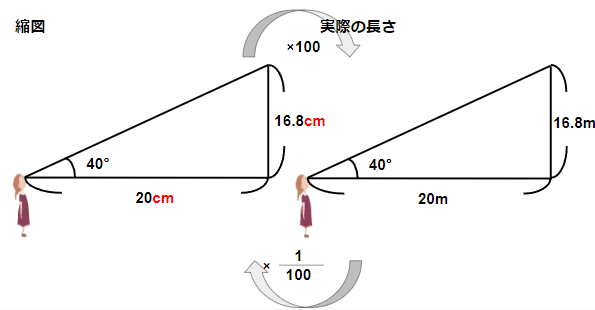
縮図の長さを100倍したら実際の長さになるから、
縮図の16.8cmは、実際の16.8×100=16800cmということ。
16800cmというのは16.8mのことだから、
実際の高さは16.8mと求めることができるよ。
STEP6 建物の高さを求めよう
最初の図に、今回わかった16.8mを書き入れてみよう。
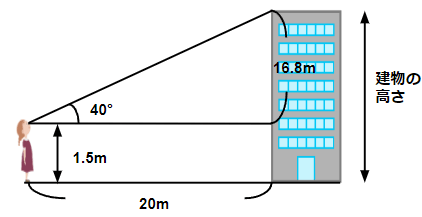
答えを「建物の高さは16.8m」としてしまったら間違いだったね。
上の図をみてわかるとおり、人の目線の高さを足さないといけないよね。
だから16.8に1.5を足すよ。
16.8+1.5=18.3
建物の高さは18.3mと求めることができるね。
「縮図を利用した問題の解き方」まとめ
- STEP1 問題文から、図を簡単に書こう
- STEP2 縮図を書くために縮尺を決めよう(例:\(\frac{1}{100}\))
- STPE3 決めた縮尺をもとに縮図を書こう
- STEP4 縮図の長さ(求める部分)を実際に定規で測ってみよう
- STEP5 測った長さから、実際の長さを求めよう(例:100倍)
- STEP6 目線の高さなど、足さなければいけない長さを足そう
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。