線対称な図形の書き方（マスあり）をくわしく解説「線対称の作図」
目次
線対称な図形の性質を使って線対称な図形を書こう
「線対称な図形」とは、ある線で折った時にピッタリ重なる図形のことだったよね。
今回は「線対称な図形」を書く方法を、３つの図形の書き方を確認しながら解説するよ。
線対称な図形を書こう①
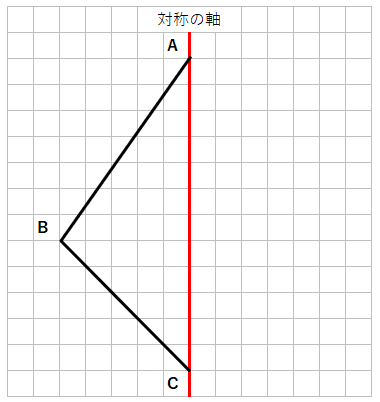
下の三角形ABCと、線対称な三角形ADCを書きなさい。
線対称な図形の書き方を考えるために、線対称な図形の性質をおさらいしよう。
この性質をわかっていないと、もう少し難しい問題になったときにつまづいてしまうよ。
線対称な図形と対称の軸の関係
- 線対称な図形では、
対応する「２つの点を結ぶ直線（青い線・緑の線）」は、
対称の軸と垂直に交わる。
- 交わる点（点G・点H）から対応する２つの点までの長さは等しくなる。
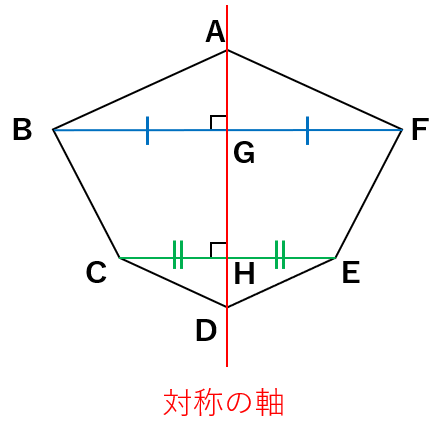
線対称な図形を書くときのポイントは「垂直」と「長さが等しい」ということを覚えておこう。
STEP1～3の順番で線対称な図形を書いていくよ。
STEP1 「対応する点同士を結んだ線」と「対称の軸」が垂直
「対応する点同士を結んだ線」は対称の軸に垂直になるのだから、
まず、点Bから対称の軸に垂直な線を引こう。
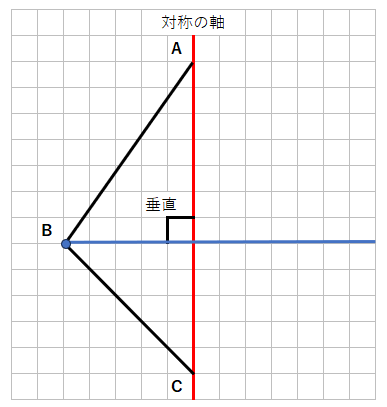
青の線のどこかに、点Bに対応する点があるってことだね。
では、STEP2で点Bに対応する点を見つけよう。
STEP2 「対称の軸と交わる点」から「対応する２つの点」までの長さは等しい
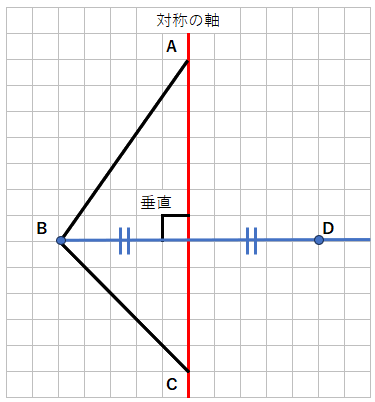
対称の軸と交わる点から、対応する２つの点（BとD）までの長さが等しいんだよね。
ということは、対称の軸から左に５マスのところに点Bがあるから、
右に５マスのところが点Dになるよ。
STEP3 点を線で結ぶ
最後に点を線で結んだら、線対称な三角形ADCの完成だよ。
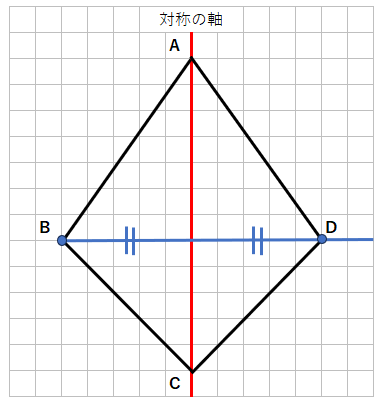
対称の軸で折ったら、ピッタリ重なることがわかるね。
今回の問題では、点Aと点Cは対称の軸の上に乗っていたから何も考えなくてよかったね。
でも、問題によっては、いろいろ考えなくてはいけない点が増えたりするよ。
線対称な図形を書こう②「対応する点が多い図形」
下の図形と線対称な図形を書きなさい。
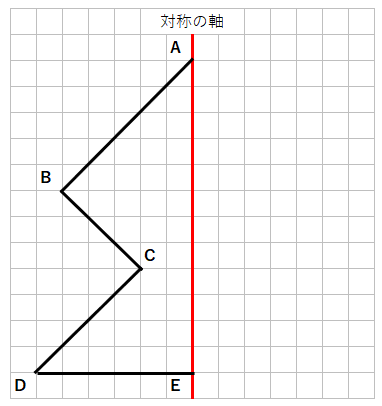
さっきより、複雑な形だね。だけどやることは同じだよ。
まず、点Bと点Cと点Dの対応する点を見つけよう。
（点Aと点Eは、対称の軸の上に乗っているから考える必要はないよ）
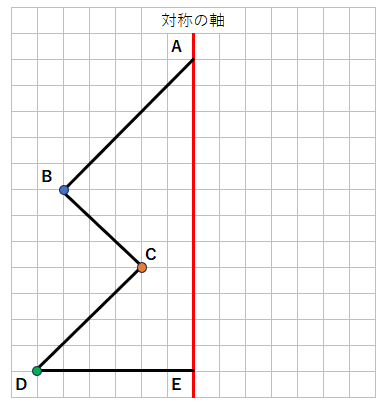
STEP1 「対応する点同士を結んだ線」と「対称の軸」が垂直
「対応する点同士を結んだ線」は対称の軸に垂直になるのだから、
まず、点Bと点Cと点Dから対称の軸に垂直な線を引こう。
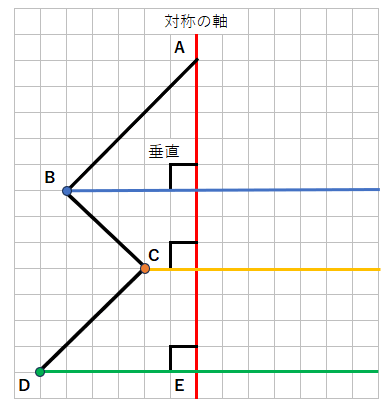
青の線、黄色の線、緑の線のどこかに、点B、点C、点Dに対応する点があるということだね。
STEP2 「対称の軸と交わる点」から「対応する２つの点」までの長さは等しい
点B、点C、点Dそれぞれに対応する点を
点F、点G、点Hとしよう。
対称の軸から
・左に５マスのところに点B
・左に２マスのところに点C
・左に６マスのところに点D
があるから、
線対称な図形は
・右に５マスのところに点F
・右に２マスのところに点G
・右に６マスのところに点H
ができるよ。
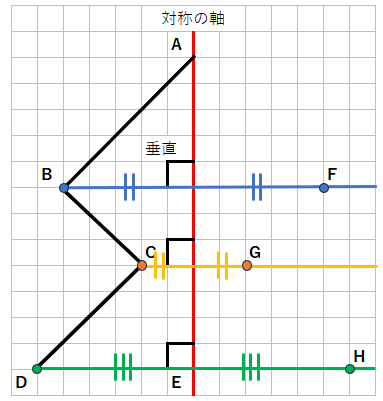
STEP3 点を線で結ぶ
最後に点を線で結んだら、線対称な図形の完成だよ。
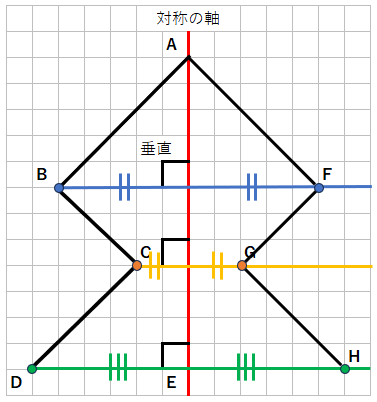
対称の軸で折ったら、ピッタリ重なることがわかるね。
今回の問題は、３つの点の対応する点を見つけ出さなくちゃいけなかったから、少し複雑だったね。
線対称な図形を書こう③「対称の軸が横になる図形」
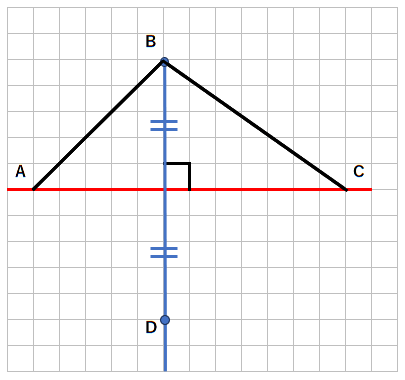
下の図形と線対称な図形を書きなさい。
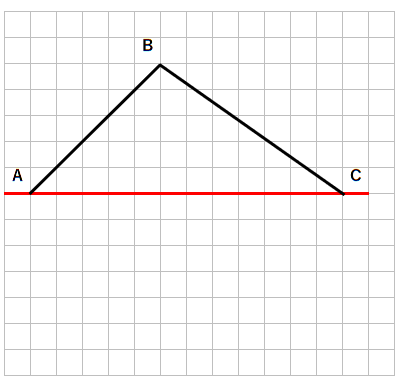
これまでは対称の軸が縦だったけれど、今度の問題は横になっているね。
ただ、やることは今までと同じだよ。
STEP１ 「対応する点同士を結んだ線」と「対称の軸」が垂直
「対応する点同士を結んだ線」は対称の軸に垂直になるのだから、
まず、点Bから対称の軸に垂直な線を引こう。
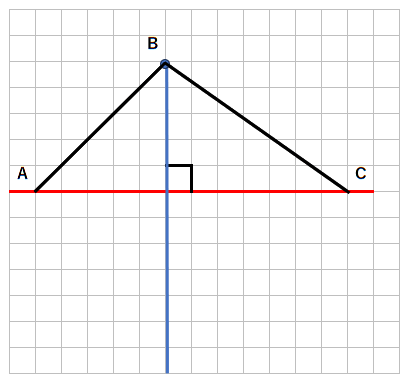
青の線のどこかに、点Bに対応する点があるってことだよ。
STEP2 「対称の軸と交わる点」から「対応する２つの点」までの長さは等しい
点Bに対応する点を点Dとしよう。
対称の軸から上に５マスのところに点Bがあるから、
下に５マスのところが点Dになるよ。
STEP3 点を線で結ぶ
最後に点を線で結んだら、線対称な図形の完成だよ。
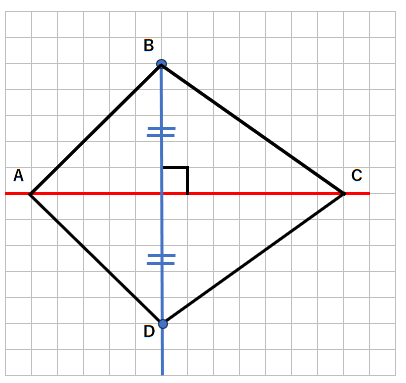
対称の軸で折ったら、ピッタリ重なることがわかるね。
今回の問題では、対称の軸が横向きだったね。中学生になると、対称の軸が斜めというバージョンも登場するよ。
ただ、線対称な図形と対称の軸の関係さえ知っていればこわくないから、必ず性質は覚えておこうね。
線対称な図形の書き方のまとめ
線対称な図形の書き方を最後に復習しよう。
①「対応する点同士を結んだ線」と対称の軸は垂直になる性質から、対称の軸に垂直な線を引く
②「対称の軸と交わる点」から「対応する２つの点」までの長さは等しい性質から、同じ長さ分のところに点を打つ
③点を線で結ぶ
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
