「比例の利用」比例の文章問題の解き方をくわしく解説（練習問題）
小学校６年生の算数で学習する「比例の利用」について、比例の文章問題の解き方のポイントをわかりやすく解説するよ。
それぞれの問題のパターンごとに、どのように比例を利用すれば良いのか、どのような考え方をすれば良いのか確認しよう。
目次
紙の枚数を「比例」を利用して求める問題
同じ種類の紙がたくさんあったとしよう。
この紙の枚数を簡単に数えるにはどうしたらいいかわかるかな？
１枚、２枚、３枚・・・と数えてもいいんだけど大変だよね。
そんなときに「比例」を使って考えよう。
同じ種類の紙だから
紙の枚数が２倍、３倍・・・になったら
紙の重さも２倍、３倍・・・になるよね。
まさに「比例」だね。
紙の重さを測って、枚数を求める
じゃあ、紙の重さを測って枚数を求めてみよう。
同じ種類の紙がたくさんあります。
すべての紙の重さは５００ｇでした。
１０枚の紙の重さが５０ｇだったとき、すべての紙の枚数を求めなさい。
問題文に書いてあることを表にすると次のようになるよ。
すべての紙の枚数の求め方を３つ紹介するね。
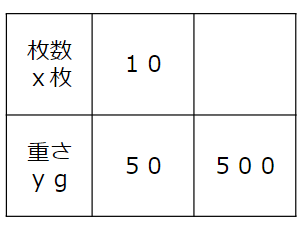
求め方①
枚数と重さは比例の関係にあるんだったよね。
ということは
枚数が２倍、３倍になったら、重さも２倍、３倍になる。
重さは５０から５００で１０倍になっているから、
枚数も１０倍して、１０×１０＝１００枚ということがわかるね。
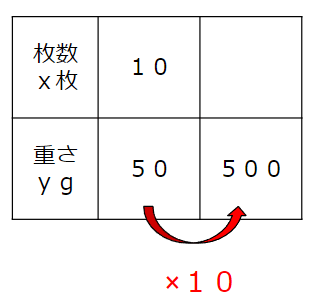
求め方②
１０枚で５０ｇということは、
１枚で５ｇってことがわかるよね。
（５０÷１０で求められるね）
表に書くと次の通りだよ。
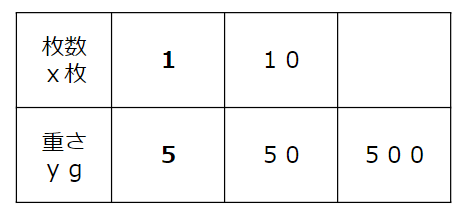
紙の枚数と重さは比例の関係にあるから
枚数が２倍、３倍になったら、重さも２倍、３倍になるよね。
重さは５から５００で１００倍になっているから、
枚数も１００倍して、１×１００＝１００枚ということがわかるね。
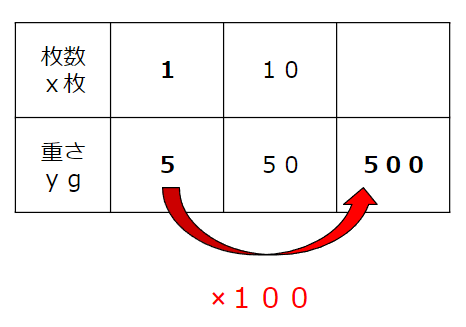
求め方③
枚数と重さは比例の関係にあるんだったよね。
比例の式を思い出してみよう。
比例の式
ｙ＝決まった数×ｘ
例えば、下のような表だったら、
ｘを５倍したらｙになるから
ｙ＝５×ｘという式になる。
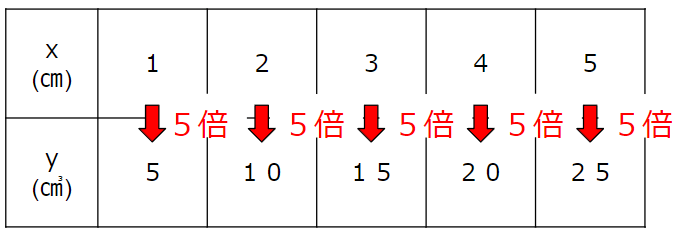
紙の枚数と重さの表は次の通りだよ。
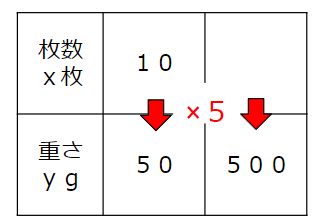
ｘを５倍したらｙになっていることがわかるね。
ということは、
すべての枚数は
５００÷５で求められるよね。
だから、１００枚ということがわかるよ。
紙の重さを測って、枚数を求める問題のまとめ
３つの求め方で紙の枚数を考えたよね。
ここでやり方を振り返ろう。
どれも比例の性質を使っていることを確認しておこう。
やり方① ｙが１０倍になるからｘも１０倍にする
やり方② １枚の重さを求める
やり方③ ｘを何倍したらｙになるかを考える
今の問題は
すべての紙の枚数を数えるために、
紙の枚数と重さが比例することを使って求めたよね。
紙の厚さを測って、枚数を求める
じゃあ、今度は
紙の枚数と紙の厚さで考えてみよう。
当たり前だけど、
紙の枚数が２倍、３倍・・・となると
紙の厚さも２倍、３倍・・・になるよね。
枚数と厚さも比例していることがわかるね。
じゃあ、紙の厚さを測って枚数を求めてみよう。
同じ種類の紙がたくさんあります。
すべての紙の厚さを測ったところ、厚さは３０mmでした。
４０枚の紙の厚さが１２mmのとき、紙の枚数を求めなさい。
問題文に書いてあることを表にすると次のようになるね。
さっきと同じで
すべての紙の枚数の求め方を３つ紹介するね。
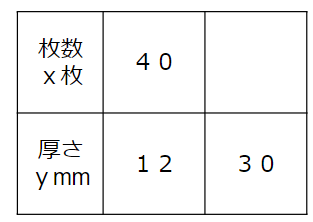
求め方①
枚数と厚さは比例の関係にあるんだったよね。
ということは
枚数が２倍、３倍になったら、厚さも２倍、３倍になる。
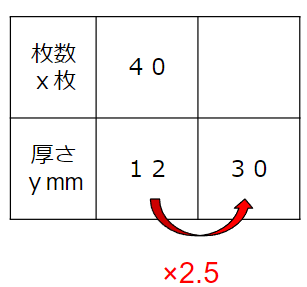
厚さは12から30で何倍になっているかな？
少し計算がめんどうだけど、
30÷12=2.5倍
と求められるよ。
だから枚数も2.5倍して、40×2.5＝100枚ということがわかるね。
求め方②
40枚で12ｇということは、
1枚で0.3ｇってことがわかるよね。
（求め方は12÷40だよ）
表に書くと次の通りだよ。
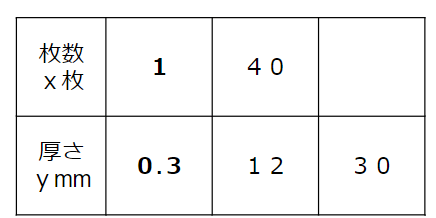
紙の枚数と厚さは比例の関係にあるから
枚数が２倍、３倍になったら、厚さも２倍、３倍になるよね。
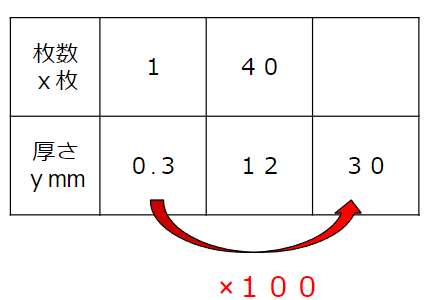
厚さは0.3から30で100倍になっているから、
枚数も100倍して、1×100＝100枚ということがわかるね。
求め方③
枚数と厚さは比例の関係にあるんだったよね。
紙の枚数と厚さの表は次の通りだよ。
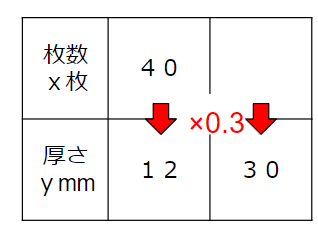
ｘを0.3倍したらｙになっていることがわかるね。
（12÷40で求められるよ）
ということは、
すべての枚数は
30÷0.3で求められるよね。
だから100枚ということがわかるよ。
紙の厚さを測って、枚数を求める問題のまとめ
３つの求め方で紙の枚数を考えたよね。
ここでやり方を振り返ろう。
どれも比例の性質を使っていることを確認しておこう。
やり方① ｙが2.5倍になるからｘも2.5倍にする
やり方② １枚の重さを求める
やり方③ ｘを何倍したらｙになるかを考える
紙の枚数を「比例」を利用して求める問題のまとめ
たくさんの紙の枚数を
１枚１枚数えない方法を２つ紹介したよ。
・重さを測って比例の性質を使う
・厚さを測って比例の性質を使う
比例の性質を使うことで、
大変な作業でも簡単に答えを求めることができるんだ。
木の高さを「比例」を利用して求める問題
木の高さって測るのは難しいよね。
小さい木ならなんとか測れるけれど・・・
大きい木だと「はしご」が必要になるし、危ない作業だよね。
そんなときに、「比例」の性質を利用することで 簡単に木の高さを求めることができるんだ。
実は、「実際の長さ」と「かげの長さ」は比例しているんだ
公園にいる身長1.7mの人のかげの長さが1mのとき、同じ公園にある木のかげの長さが5ｍだった。この木の高さを求めよ。
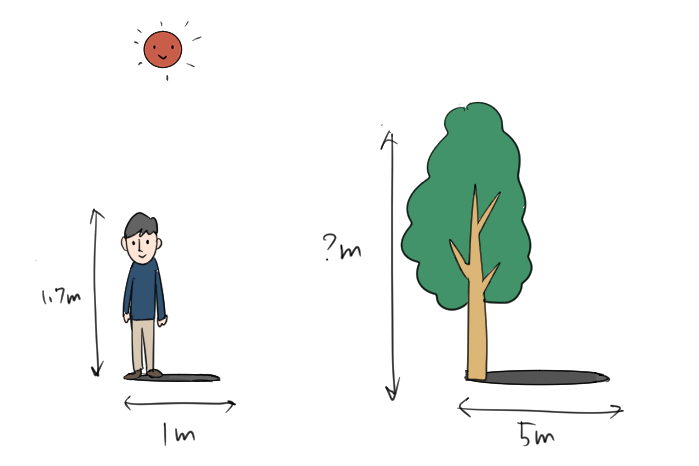
文章に書いてある長さを表にすると次のようになるよ。
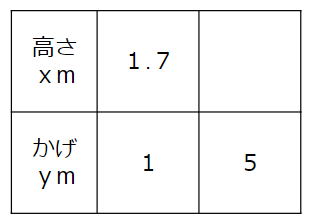
「高さ」と「かげ」は比例の関係にあるんだったよね。
ということは
「高さ」が２倍、３倍になったら、「かげ」も２倍、３倍になる。
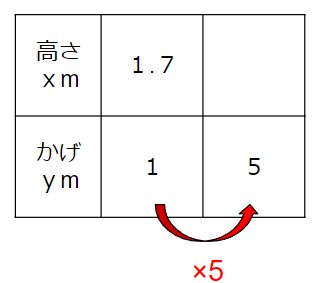
「かげ」は1から5で5倍になっているから
「高さ」も5倍して、1.7×5＝8.5mということがわかるね。
針金の長さを「比例」を利用して求める問題
針金アートって知っているかな？
針金を折り曲げたりして作った作品のことだよ。
次のような針金で作った犬を考えてみよう。
作ったあとに、
「この針金の長さは何mだった」と聞かれたら・・・
「一回元通りにしないとだめじゃん」
「あーあ、せっかく作ったのにな」と思うよね。
ただ、比例の性質を使えば、簡単に針金の長さを求めることができるんだ。
針金の長さが２倍、３倍・・・となると
重さも２倍、３倍・・・になるから
長さと重さは比例しているよ。
じゃあ、重さを測って針金の長さを求めてみよう。
次のような針金の犬を作りました。
針金の犬の重さを測ると６０ｇでした。
犬を作るのに使った針金の長さを求めなさい。
ただし、針金の重さは１ｍで５ｇです。
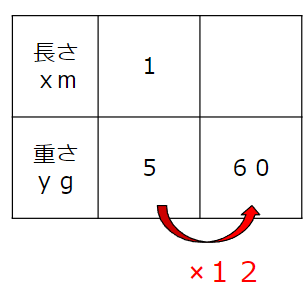
わかっていることを表にすると次の通りだよ。
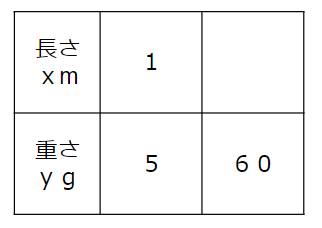
長さと重さは比例の関係にあるんだったよね。
ということは
長さが２倍、３倍になったら、重さも２倍、３倍になる。
重さは５から６０で１２倍になっているから
長さも１２倍して、１×１２＝１２ｍということがわかるね。
「比の利用」比の文章問題の解き方 まとめ
- まずは問題の文章から読み取れる「わかっている数」をｘとｙとして表に整理しよう。
「求める数（わからない数）」の部分は、空らんで大丈夫だよ。 - 「求める数（わからない数）」を、つぎの３つのやり方で求めよう。
- やり方① ｙが〇倍になることからｘも〇倍にする
- やり方② ｘが「１」のときの「ｙ」を求める
- やり方③ ｘを何倍したらｙになるかを考える
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
