「比例の性質」とは？分数倍・小数倍で比例を表す方法（練習問題）

小学校６年生で学習する「比例の性質」について、これまでの「整数倍」に加えて、「分数倍」「小数倍」で比例する２つの数量の関係を表す方法をわかりやすく解説するよ。

比例の性質を使った練習問題にもチャレンジしよう。

「比例の性質」とは？ 分数倍・小数倍で比例を表す方法（練習問題）のPDF（13枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 比例する２つの数量の関係
• 比例の性質
• 比例の性質を使った問題
• 比例の性質のまとめ

比例する２つの数量の関係

「比例」については、小学５年生でも勉強したよね。
一度、「比例とはなんだったか」復習してみよう。

比例の復習

比例とは

２つの量があり、
一方が２倍、３倍・・・となると、
それにともなって
もう一方も２倍、３倍・・・となるもの

たとえば１つ１００円のリンゴを買うとき、買ったリンゴの個数が２倍、３倍になると、もちろん支払う金額も２倍、３倍になるよね。

このときの「買ったリンゴの個数」と「値段」は比例の関係といえるよ。

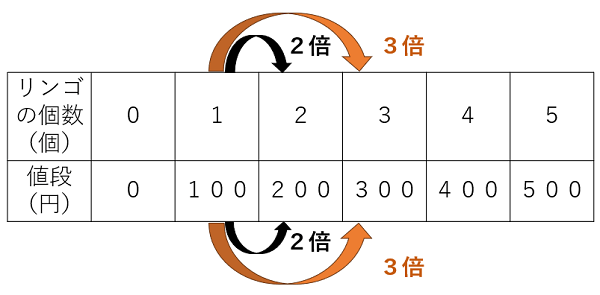
表にすると、一方が２倍、３倍になるともう一方も２倍、３倍になっているので、比例の関係であることがよくわかるね。

小学５年生で習った「比例」を、どうしてまた小学６年生でも学習するのかというと、小学６年生のの比例ではさらに「小数倍」「分数倍」の場合を考えるんだ。

小学５年生の比例では、さっきの「リンゴの個数」と「値段」のように、
「２」倍、「３」倍・・・という「整数倍」しか登場しなかったよね。

小学６年生で学習する比例では、0.2倍、0.3倍・・・や\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍・・・のような「小数倍」や「分数倍」が登場するんだ。

比例する２つの数量の関係（整数倍で表す）

さっきの「リンゴを買った時の値段」について、リンゴの個数をｘ、値段をｙとして考えてみよう。
※小学６年生からの比例では、２つの数量を「ｘ」と「ｙ」にしていくよ。

ｘ（リンゴの個数）が「２」と「４」の部分に注目しよう。

ｘが「２」から「４」になるには、何倍になっているかな？
そしてこのとき、ｙは何倍になっているかな？

たろう

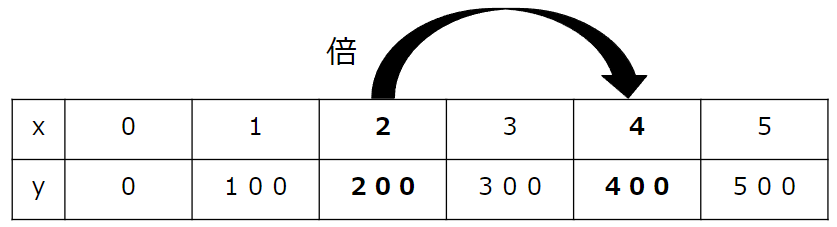
簡単だよ。
２から４だから、２倍に決まっているよ。

では、どうやって２倍と求めることができるのか、確認してみよう。

ｘは何倍になっているか

「何倍になっているか？」を求めるには、「比べる量÷もとにする量」を考えればよかったね。

ｘは２から４になっているのだから、
４÷２＝２倍と求めることができるよ。

ｙは何倍になっているか

同じく、ｙは２００から４００になっているのだから、
４００÷２００＝２倍と求めることができるね。

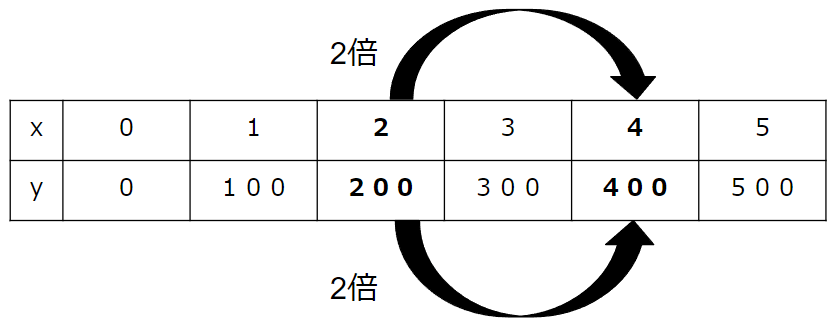
ｘが２倍になると、ｙも２倍になっていることがわかるね。

それでは今度は「小数倍」や「整数倍」の問題も考えていこう。

比例する２つの数量の関係（分数倍で表す）

ｘ（リンゴの個数）が「３」と「５」の部分に注目しよう。

ｘが３から５になるには、何倍になっているのかな？
そしてこのとき、ｙは何倍になっているかな？

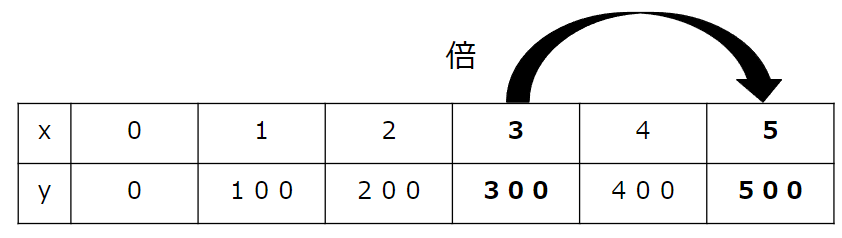
ｘは何倍になっているか

ｘが３から５になっているのだから、
５÷３で求めることができるね。
ただ、さっきと違うのは、「５÷３は割り切れない」こと。

「割り切れない」ときは、分数を使って表せばよかったね。
÷の後の整数は分母にくるから、
５÷３＝\(\frac{５}{３}\)倍と表すことができるね。

ｙは何倍になっているか

同じようにｙは３００から５００になっているのだから
５００÷３００＝\(\frac{５００}{３００}\)＝\(\frac{５}{３}\)倍と表すことができるよ。

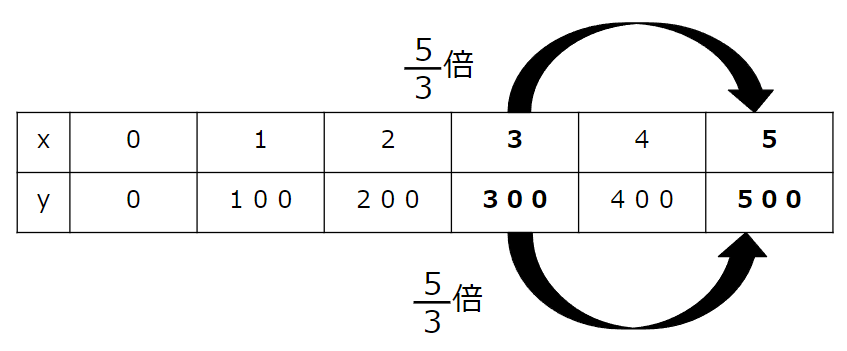
ｘが\(\frac{５}{３}\)倍になると、ｙも\(\frac{５}{３}\)倍になっていることがわかるね。

このように、今まで整数倍でしか表してこなかった比例を、分数倍でも表すことができたね。

比例する２つの数量の関係（小数倍で表す）

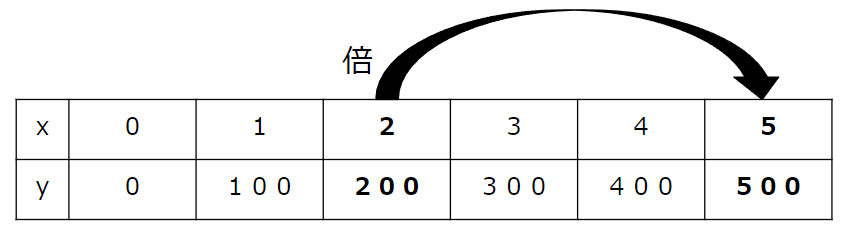
ｘ（リンゴの個数）が「２」と「５」の部分に注目しよう。

ｘが２から５になるには、何倍になっているのかな？
そしてこのとき、ｙは何倍になっているかな？

ｘは何倍になっているか

ｘが2から5になっているのだから、
5÷2で求めることができるね。

やっぱり割り切ることができないのだけれど、今回は小数を使って表してみよう。
5÷2＝2.5倍と表すことができるね。

ｙは何倍になっているか

同じようにyは200から500になっているのだから、
500÷200で求められるよ。

小数を使って表すと
500÷200＝2.5倍と表すことができるね。

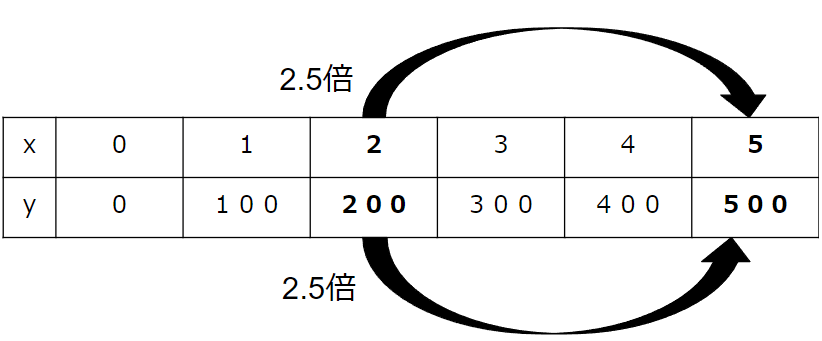
xが2.5倍になると、yも2.5倍になっていることがわかるね。

今まで整数倍でしか表してこなかった比例を、小数倍でも表すことができたね。

これまでｘの値が増える場合だけを見てきたけれど、ｘの値が減る場合も確認しておこう。

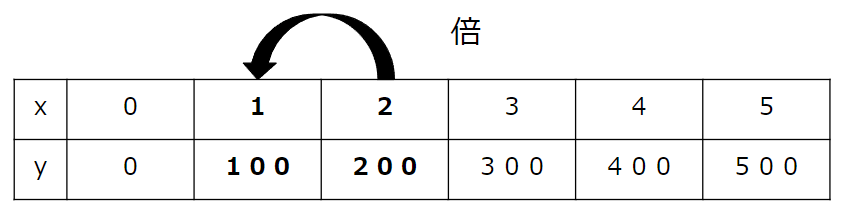
ｘ（リンゴの個数）が「２」と「１」の部分に注目しよう。

ｘが２から１になるには、何倍になっているのかな？
そしてこのとき、ｙは何倍になっているかな？

ｘは何倍になっているか

ｘが２から１になっているのだから、
１÷２で求められるよ。
まちがえて、２÷１＝２倍にしないようにね。
２から１で減っているのに「２倍」はおかしいよね。

１÷２を分数で表すと
１÷２＝\(\frac{１}{２}\)倍となるね。

ｙは何倍になっているか

同じようにｙは２００から１００になっているのだから
１００÷２００＝\(\frac{１００}{２００}\)＝\(\frac{１}{２}\)倍と表すことができるよ。

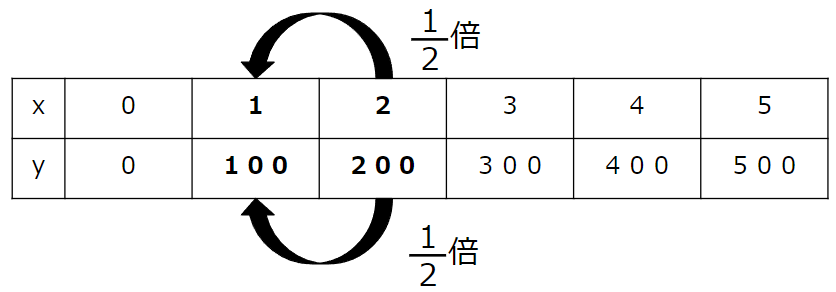
ｘが\(\frac{１}{２}\)倍になると、ｙも\(\frac{１}{２}\)倍になっていることがわかるね。

４つの問題のｘとｙの関係をまとめると次のようになるよ。

４つのことから、比例の性質がなんとなくわかったかな？

比例の性質

小学５年生では、次のように「整数倍」の場合しか考えてこなかったね。

ただ、今回「小数倍」や「分数倍」でも
一方が〇倍となると、もう一方も〇倍になることがわかったね。

だから、小学校６年生からは「比例の性質」は次のようにバージョンアップされるよ。

だから、ｘとｙが比例の関係にあるとき、

• ｘが３９倍されたら、ｙも３９倍
• ｘが\(\frac{１}{５０}\)倍されたら、ｙも\(\frac{１}{５０}\)倍
• ｘが0.99倍されたら、ｙも0.99倍

ということがわかるよ。

では、比例の性質を使った問題に挑戦してみよう。

比例の性質を使った問題

水道の蛇口をひねった時、１分で４ｃｍの深さずつ水が入ります。

下の表は時間ｘ分と水の深さｙｃｍの関係を表しています。
５分後の水の深さを求めなさい。

たろう

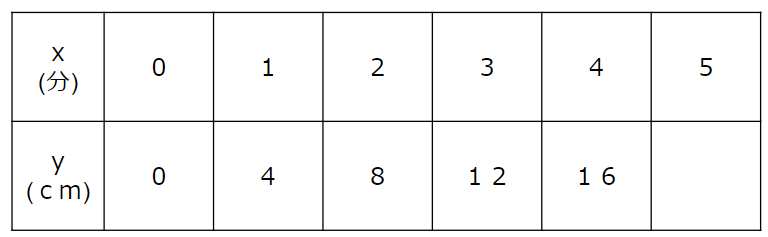
簡単だよ。
１分で４ｃｍずつ増えるんだから、５分の時は４×５で２０ｃｍだよね。

確かにその通り。
ただ、今回は比例の性質に注目して、「ｘが何倍になっているか」を考えてから答えを求めてみるよ。

ｘが１から５になっているところに注目しよう。

ｘは何倍になっているか

ｘが１から５になっているのだから、
５÷１＝５倍と求められるよ。

ということは、比例の性質から「ｙも５倍になる」ということだよね。

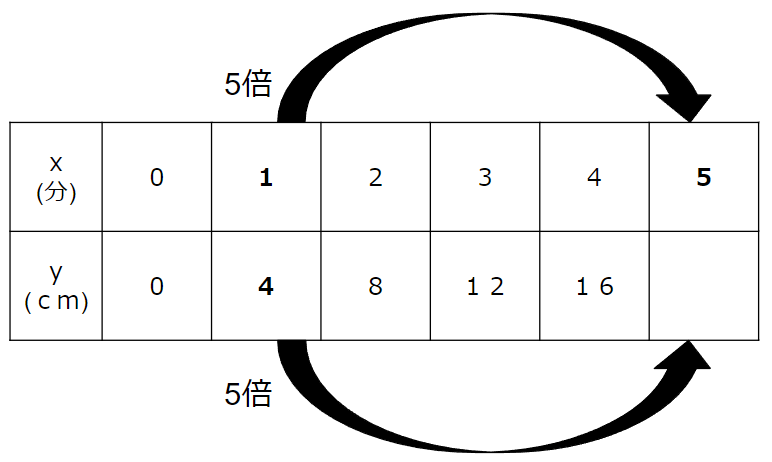
「ｙも５倍になる」をもとにｙを求めよう

ｙも５倍になるのだから、ｙは４を５倍して
４×５＝２０ｃｍ
と求めることができるね。

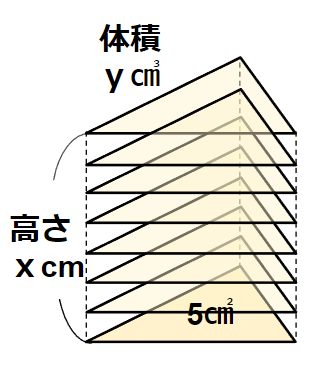
下の表は底面積が４cm²の三角柱の
高さｘcm、体積ｙcm³の関係を表したものです。
高さ５cmのときの体積は、高さ２cmのときの体積の何倍ですか。

比べる量÷もとにする量で求める

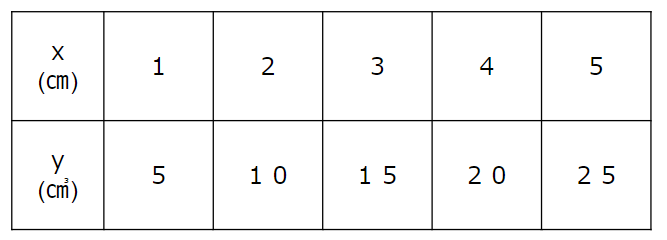
高さ５cmのときの体積２５cm³
高さ２cmのときの体積１０cm³
だから、次のように考えたらいいよね。

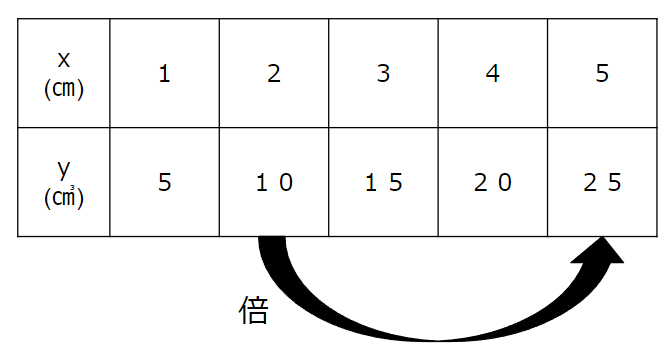
体積ｙは１０から２５になっているから、
分数で表すなら
２５÷１０＝\(\frac{２５}{１０}\)＝\(\frac{５}{２}\)倍
小数で表すなら
２５÷１０＝２.５倍
になるよ。

比例の性質を利用して求める

今回の問題は、ｘの方が数字が小さいから、ｘに注目する方法もあるよ。

なぜｘに注目しても平気かというと、比例の性質「ｘの値が〇倍されると、それに対応するｙの値も〇倍になる」ことから、ｘが何倍になったかを求めれば、ｙが何倍になるかもわかるからだよね。

ｘが２から５になっているので、
５÷２＝\(\frac{５}{２}\)倍になっていることがわかるよ。

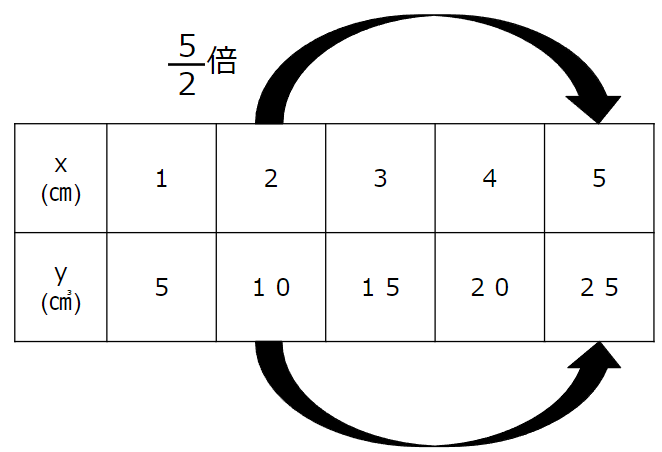
だから、ｙも\(\frac{５}{２}\)倍になる、と求めることができるね。

比例の性質のまとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。