「比例のグラフの書き方」なぜ直線なのか特徴をわかりやすく解説　

小学校６年生の算数で学習する「比例のグラフ」について、比例の関係をグラフに表すにはどうすればよいか、比例のグラフはなぜ直線になるのか、比例のグラフにはどんな特徴があるのかをわかりやすく解説するよ。

比例のグラフからどんなことが読み取れるのかも紹介していくよ。

「比例のグラフの書き方」 なぜ直線なのか特徴をわかりやすく解説のPDF（15枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 比例の関係をグラフに表そう
• 比例のグラフが直線になる理由
• 比例のグラフの特徴
• 比例のグラフから読み取ってみよう
• 「比例のグラフ」まとめ

比例の関係をグラフに表そう

今まで比例の性質や比例の式について勉強してきたよね。
今回は比例の関係を「グラフ」で表わすにはどうすればいいかを学習するよ。

グラフとは

グラフといえば、今までに「折れ線グラフ」や「棒グラフ」を勉強してきたよね。
そもそもグラフとは何か？を辞書で調べると次のように書かれているよ。

おたがいに関係のある２つ以上の数量が、どういう関係なのか？をひと目でわかりやすく図にしているのがグラフなんだね。

比例では、２つの数量ｘとｙは「一方が〇倍になると、もう一方も〇倍になる」という関係だったね。
このｘとｙの関係を図で表していくということだね。

比例の関係にある２つ以上の数量をグラフに表そう①

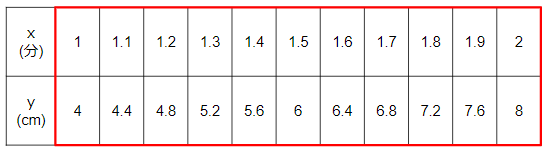
例えば、次のような「水を入れる時間ｘ分」と「水の深さｙｃｍ」は
比例の関係にあるんだったよね。

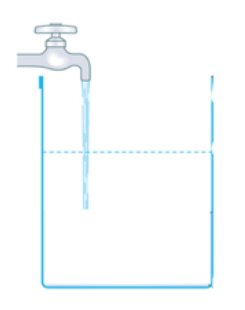
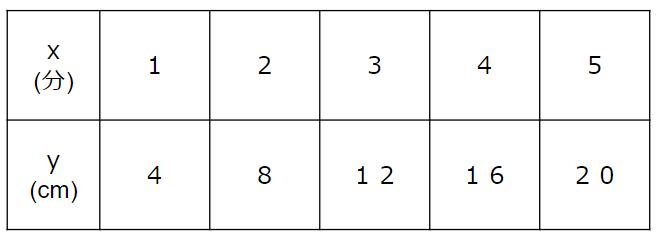
この表をもとにｘとｙの関係をグラフに表していこう。

比例の関係をグラフに表すには次の２ステップが大切だよ。

では、実際にやっていこう。

ｘとｙの値の点をとる

表を縦に見ると、ｘ＝１のときｙ＝４だよね。

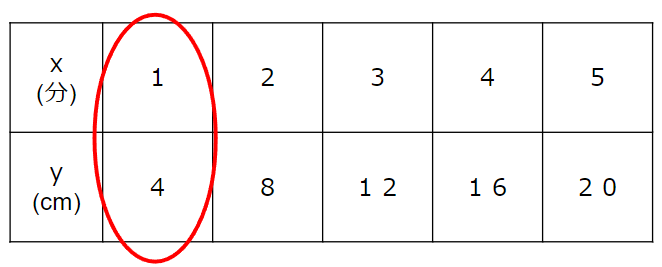
あとは他の点も順番に考えていったらOK。

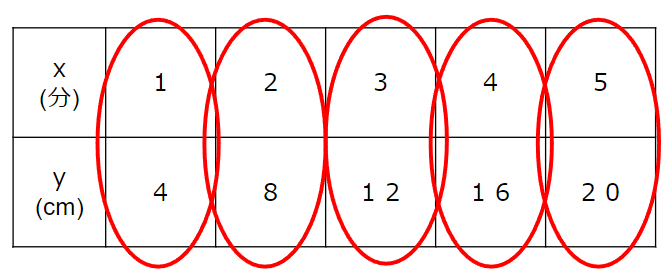
ちなみに比例の関係のグラフは、
横軸がｘの値、縦軸がｙの値だからね。

①ｘ＝１のとき、ｙ＝４
横軸が１で縦軸が４のところに点を取ろう。

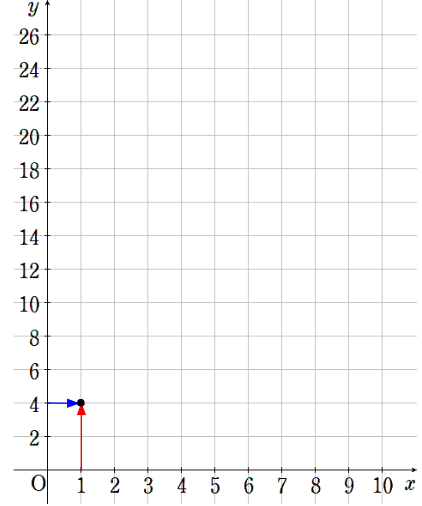
②ｘ＝２のとき、ｙ＝８

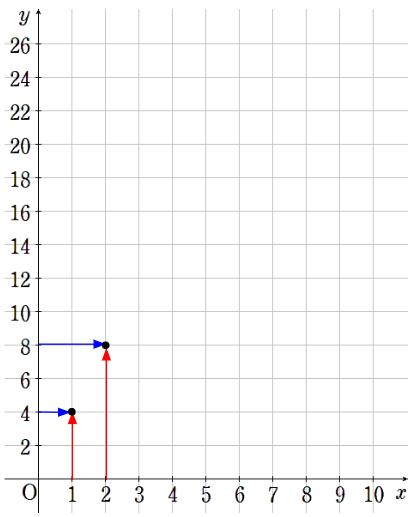
③ｘ＝３のとき、ｙ＝１２

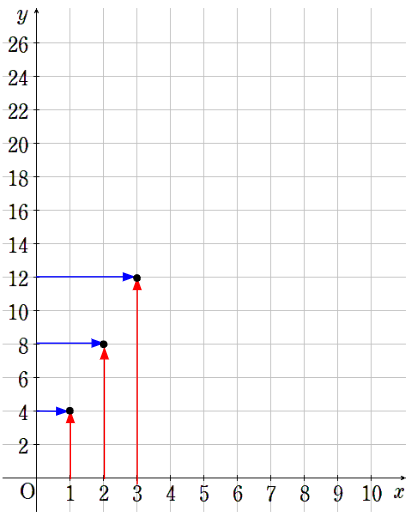
④ｘ＝４のとき、ｙ＝１６

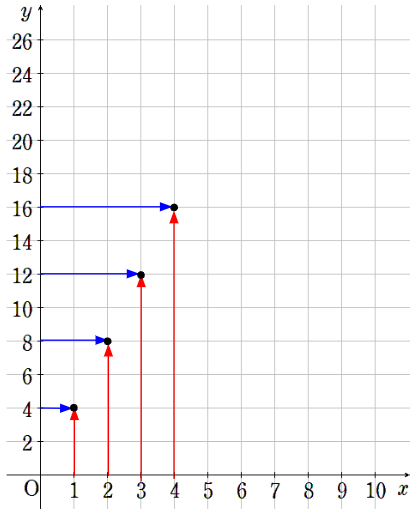
⑤ｘ＝５のとき、ｙ＝２０

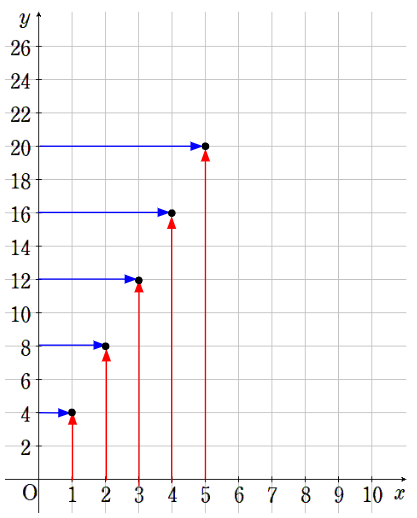
点を取り終わったら、最後に点同士を繋げるように直線を引こう。

直線を引く

すべての点を通るように
定規を使って直線を引こう。

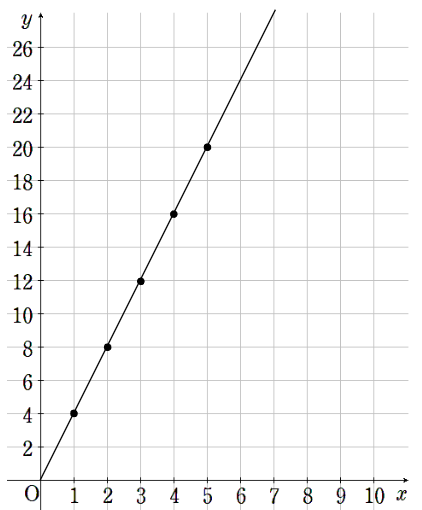
ｘ＝５より大きいところは点を取っていないけど、
直線はグラフの端まで延ばしておこう。

比例のグラフがなんで直線になるのかは後で紹介するね。

比例の関係にある２つ以上の数量をグラフに表そう②

次のような三角柱の「高さ」と「体積」も
比例の関係にあるんだったよね。

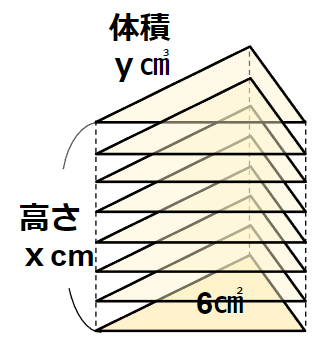
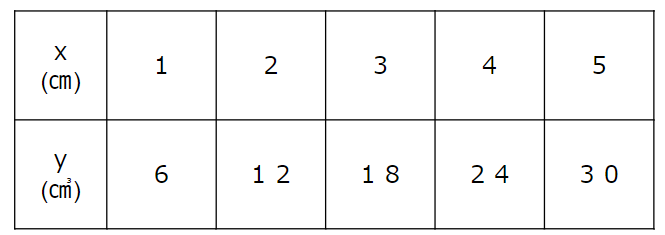
これもさっきと同じように、２ステップでグラフに表してみよう。

ｘとｙの値の点をとる

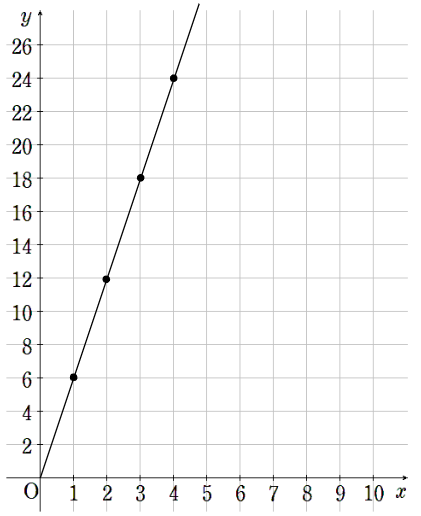
①ｘ＝１のとき、ｙ＝６
横軸が１で縦軸が６のところに点を取ろう。

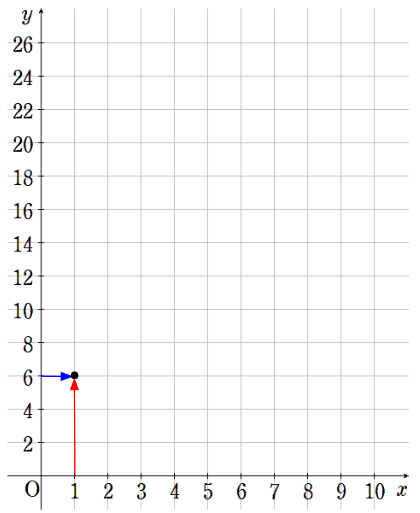
②ｘ＝２のとき、ｙ＝１２

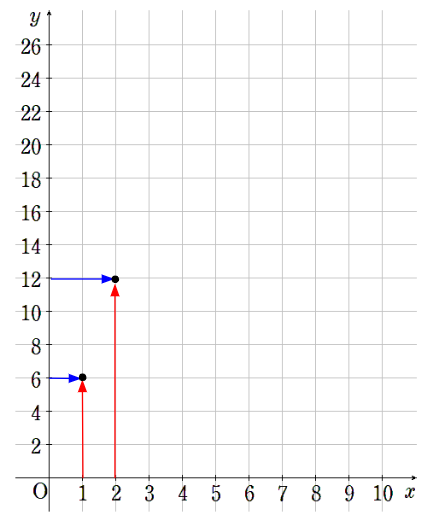
③ｘ＝３のとき、ｙ＝１８

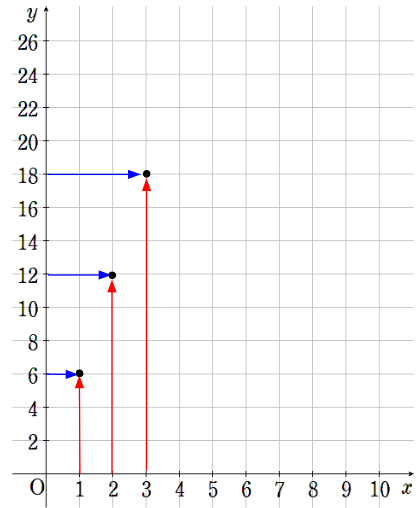
④ｘ＝４のとき、ｙ＝２４

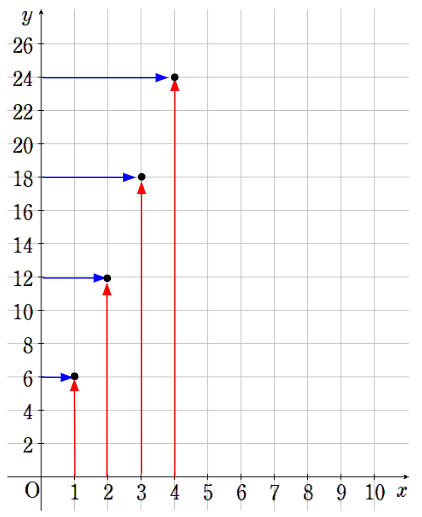
⑤ｘ＝５のとき、ｙ＝３０
ただ、グラフの縦軸が２６までしかないので、点を取ることはできないね。
だから点を取るのはこれでおしまいだね。

点を取り終わったら最後に直線を引こう。

直線を引く

すべての点を通るように
定規を使って直線を引こう。

比例のグラフが直線になる理由

比例のグラフは、どうして直線になるのだろう？

「水を入れる時間ｘ分」と「水の深さｙｃｍ」の表を見てみよう

この表からグラフに点を取ると次のようになるんだったよね。

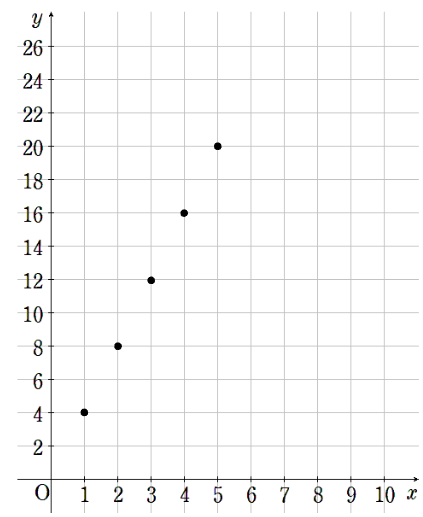
５つの点を通るんだったら、こんな線も引けてしまうよね。

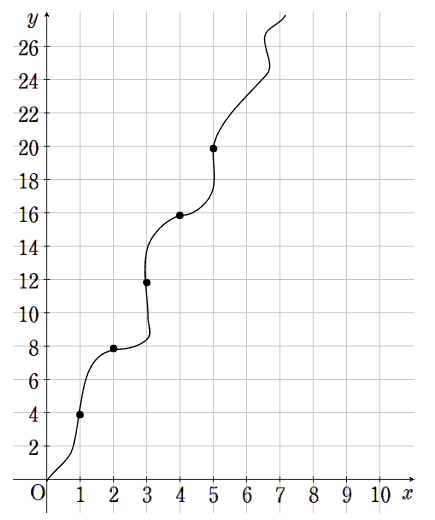
ただ、この線は間違っていて、比例のグラフは直線で結ばなければいけなかったね。

じっさいに直線になるかを確かめるために、
下の表のｘ＝１とｘ＝２の間についても、こまかく考えてみよう。

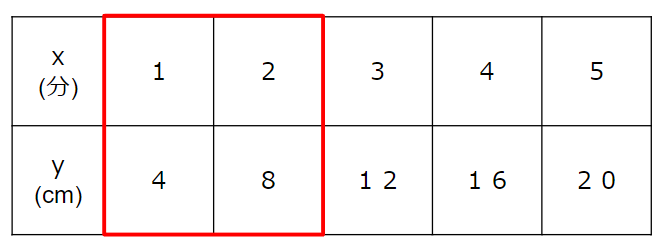
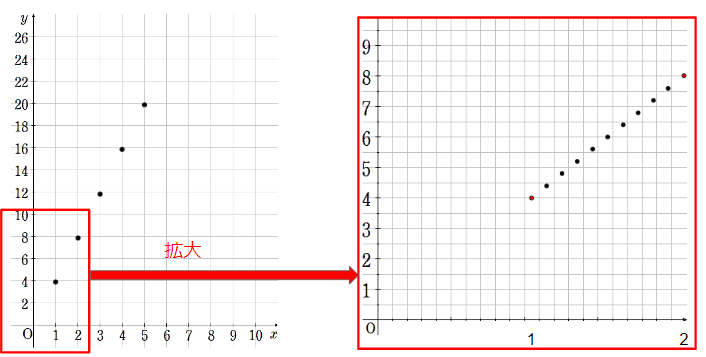
ｘ＝１からｘ＝２の間をこまかく書くと次のようになるよ。

どうやって計算したのかというと、
比例の性質どおり、ｘを４倍にするとｙになるのだから、ｘの値を順番に４倍してｙの値を求めただけだよ。

この表からグラフを書くと右のようになるよ。
左側のざっくりとしたグラフでは、２点の間はどうなるかわからなかったけれど、
右側のこまかいグラフを見ると、この２点の間もちゃんと直線になっていたことが分かるね。

比例の性質で学習したように、比例の関係にある２つの数量は「一方が〇倍になると、もう一方も〇倍になる」んだったよね。
そしてｙをｘの式で表すと、「ｙ＝決まった数×ｘ」になるんだったよね。

ということは、ｘの変化（増える、減る）に対してのｙの変化する割合はずっと一定ということなんだ。

もしこれがその時によって「ｙ＝３×ｘ」だったり、「ｙ＝６×ｘ」だったりコロコロかわるように一定でなかったら、たしかにグラフはガタガタの線になるよ。
でも、比例は「ｙ＝決まった数×ｘ」で一定だから、グラフはビシッと一直線になるんだよ。

この、比例のグラフは直線になるということはこの先の中学数学でも大切になってくるので、今回でしっかり覚えておこうね。

比例のグラフの表し方のまとめ

比例のグラフの表し方が分かったところで、
比例のグラフの特徴をまとめておこう。

比例のグラフの特徴

比例のグラフにはどんな特徴があるのだろう？
結論からいうと、比例のグラフの特徴は次の２つだよ。

直線になることはさっき確認したよね。
では「０の点を必ず通る」とはどういうことだろう？

「０の点」というのは、ｘ＝０、ｙ＝０の点のことだよ。

比例の式はｙ＝決まった数×ｘだったよね。
もし、ｘ＝０だったら、ｙ＝決まった数×０＝０になるから、ｘもｙも「０」になるということだね。

だから、比例のグラフは必ず０の点を通るんだよ。

この比例のグラフの２つの特徴は中学生になっても使うからしっかり覚えておこう。

比例のグラフから読み取ってみよう

比例の性質や式だけじゃなく、グラフのこともわかったね。
これらの知識を使って比例のグラフから読み取る問題に挑戦してみよう。

下のグラフは、けんたさんとお兄さんが自転車で走った時の、
走った時間ｘ分と走った道のりｙｍを表しています。

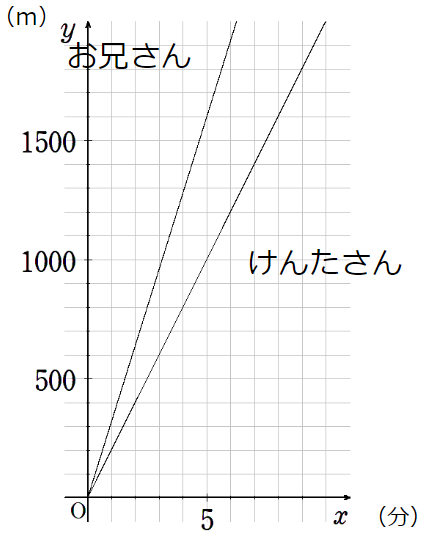
（１）けんたさんとお兄さんはどちらが速いですか。

５分のところを見てみよう。
５分間で、けんたさんは１０００ｍ、お兄さんは１６００ｍ走っているから
お兄さんの方が速いね。

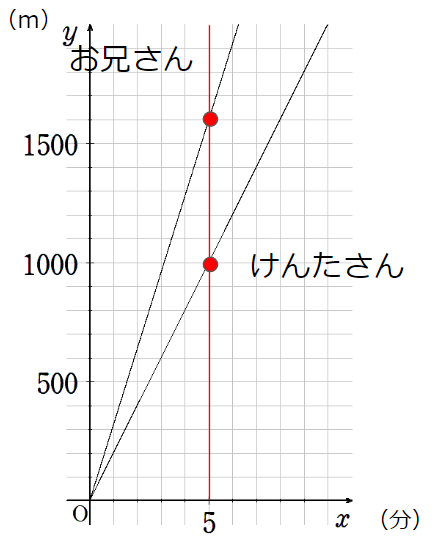
（２）１６００ｍ地点では、お兄さんが通過してから何分後にけんたさんも通過していますか。

１６００ｍ地点を通過したのは
お兄さんはスタートして５分後、
けんたさんはスタートして８分後。

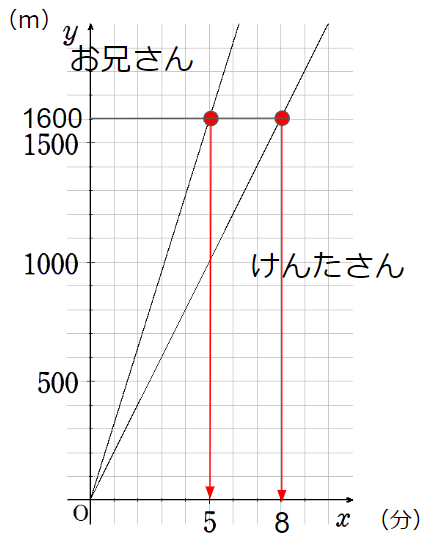
だから、お兄さんが通過して３分後にけんたさんも通過したことになるよ。

比例の関係をグラフに表すと、このように「表を見ただけではパッとわからない情報」もかんたんに読み取ることができるんだね。

「比例のグラフ」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。