「比例の式」比例の関係の式とは？決まった数の求め方（練習問題）

小学校６年生の算数で学習する「比例の式」について、比例の関係を式で表わすにはどうすればよいのか？比例の式の「決まった数」の求め方をわかりやすく解説するよ。

「比例の式」比例の関係の式とは？決まった数の求め方（練習問題）のPDF（12枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 比例の関係を式に表してみよう
• 比例の式
• 比例の式の問題
• 比例の式のまとめ

比例の関係を式に表してみよう

比例には次のような性質があったよね。

つまり、ｘの値が〇倍されると、それに対応するｙの値も〇倍になるようなｘとｙの関係が、比例の関係なんだけれど、いちいちこのように表していたら大変だよね。

そこで、今回は比例の関係を「式」に表わす方法について学習していくよ。

比例の関係にある量を２つ例にあげて解説していくね。

比例の関係にある量①

例えば、次のような「水を入れる時間」と「水の深さ」は
比例の関係にあるよ。

水を入れる時間ｘが２倍、３倍・・・になると
水の深さｙも２倍、３倍・・・になっているからね。

まあ、当たり前だよね。
水を入れる時間を２倍にしたら、水の深さも２倍になるよね。

じゃあ、ここからが今回の本題だよ。
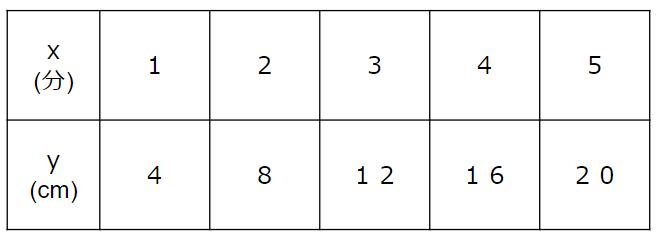
表のｘとｙの関係を式で表してみよう。

比例の関係を式で表してみよう

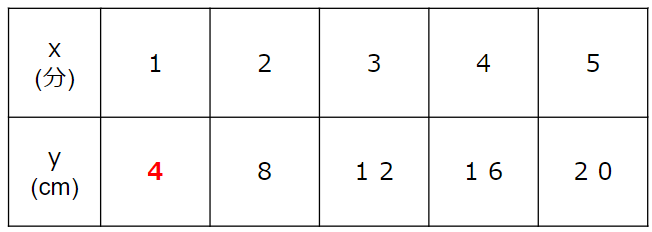
ポイントは、表を縦に見て「ｘを何倍したらｙになるか」を考えること

表を見ると、上の段（ｘ）を４倍したら、下の段（ｙ）になっていることがわかるよね。

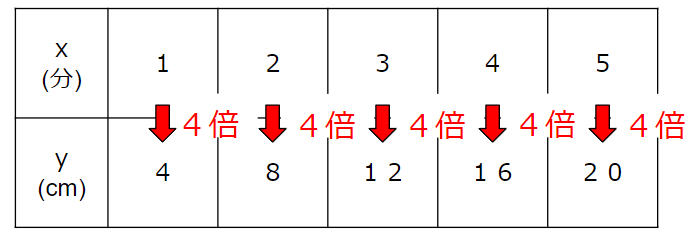
だからｙはｘを４倍した数だよね。
この関係を式にすると
ｙ＝ｘ×４

これで比例の関係を式にすることができたんだけれど、
比例では、かけ算の順番を入れ替えて
ｙ＝４×ｘ
と表すよ。

比例の関係のときに成り立つきまり

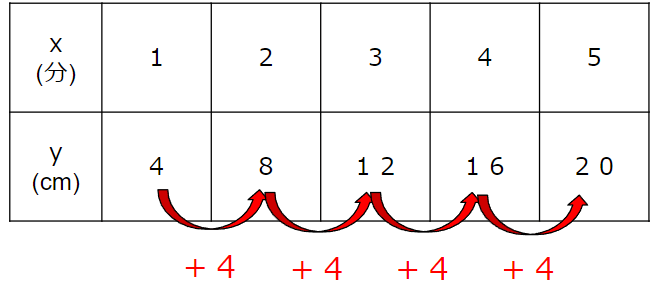
さっきの表にもどろう。

さっきは、ｘを４倍したらｙになるって考えたけど
ｙをｘで割ったらいくつになるか計算してみよう。

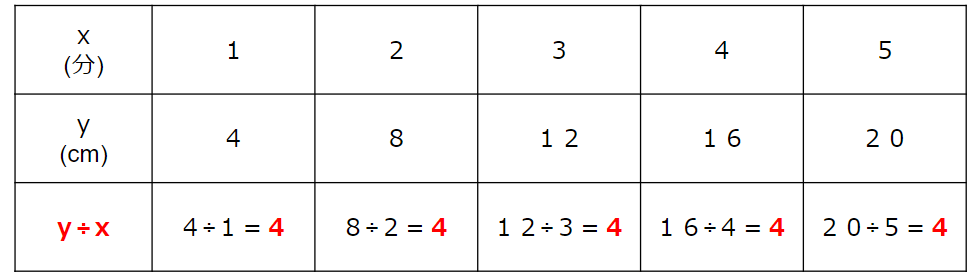
今回の問題ではｙ÷ｘを計算すると、いつも４になるんだ。

比例の関係にある量①のまとめ

「水を入れる時間」と「水の深さ」の関係で
わかったことをまとめると次のようになるよ。

「４」というのが大事な数字だということがわかるね。
では、今回の問題で「４」とは何のことなのか考えてみよう。

１分のときの水の深さ４ｃｍ

１分間で増える水の深さ４ｃｍ

くまごろう

ちなみに、中学校ではｘが１増えたときのｙの増える量のことを
「変化の割合へんかのわりあい」というよ。

比例の関係にある量②

例えば、次のような三角柱の「高さ」と「体積」も
比例の関係にあるんだ。

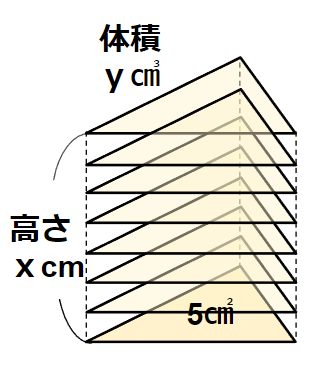
高さｘが２倍、３倍・・・になると
体積ｙも２倍、３倍・・・になっているからね。

では、表のｘとｙの関係を式で表してみよう。

比例の関係を式で表してみよう

ポイントは、
表を縦にみてｘを何倍したらｙになるかを考えることだったよね。

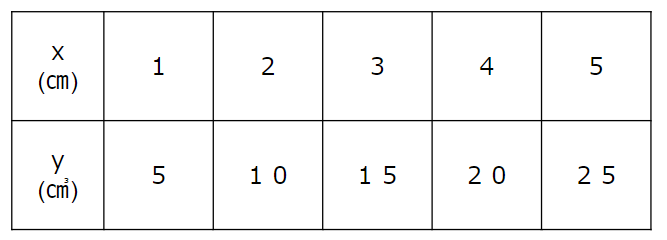
表を見ると、
上の段（ｘ）を５倍したら、下の段（ｙ）になっていることがわかるよね。

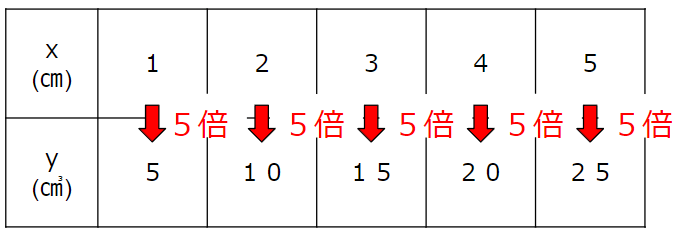
だからｙはｘを５倍した数だよね。
この関係を式にすると
ｙ＝ｘ×５

これで関係を式にすることができたんだけど、
比例では、かけ算の順番を入れ替えて
ｙ＝５×ｘ
と表すんだったね。

比例の関係のときに成り立つきまり

さっきの表にもどろう。

さっきは、ｘを５倍したらｙになるって考えたけど
ｙをｘで割ったらいくつになるか計算してみよう。

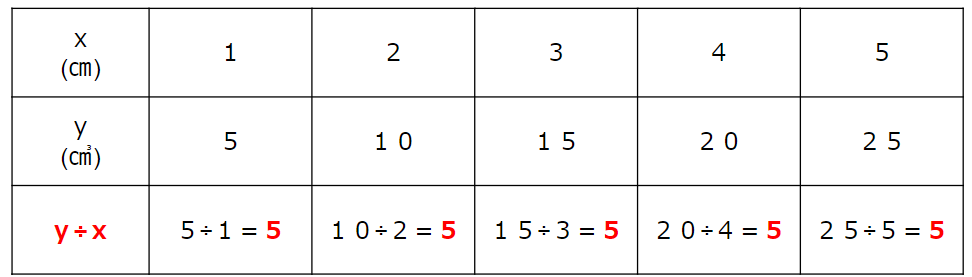
今回の問題では、ｙ÷ｘを計算すると、いつも５になるんだね。

比例の関係にある量②のまとめ

三角柱の「高さ」と「体積」の関係で
わかったことをまとめると次のようになるよ。

「５」というのが大事な数字だということがわかるね。
では、今回の問題で「５」とは何のことか考えてみよう。

高さが１ｃｍのときの体積５ｃｍ^３

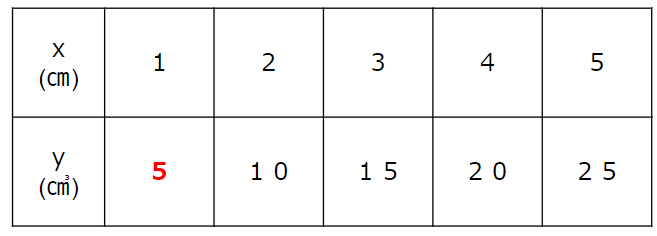
高さが１ｃｍで増えるごとに体積５ｃｍ^３増える

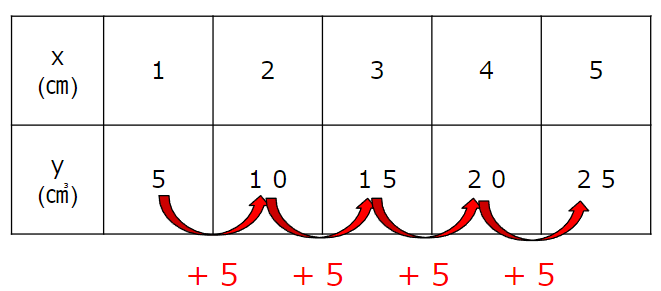
比例の式

２つの問題を振り返ってみよう。

①ｙ＝４×ｘ

②ｙ＝５×ｘ

①と②の違いは
ｘの前の数字だけだよね。

比例の式っていうのは、ｘの前の数字が変わるだけなんだ。
例えば
ｙ＝２×ｘ、ｙ＝３×ｘ、ｙ＝１０×ｘ・・・みたいな感じ。

だから、ｘの前の数字のことを「決まった数」とすると、
比例の式はひとまとめで次のように表すことができるよ。

２つの数量の関係をこのような形であらわすことができたら、それは「比例の式」だと言うことができるよ。

決まった数の求め方①

ちなみに決まった数というのは、簡単に求めることができて、
次のようにｙ÷ｘを計算すれば求まるよ。

決まった数は４だから、ｙ＝４×ｘという式になるよ。

決まった数の求め方②

求め方①では「ｙ÷ｘ」で求めたよね。
もし「ｙ÷ｘ」を忘れてしまった場合、あせらなくていいように別の求め方も覚えておこう。

ポイントは
表を縦にみてｘを何倍したらｙになるかを考えること

例えば、下の表だったら、ｘを５倍したらｙになることがわかるよね。

だから、ｙ＝５×ｘと求めることができるんだ。

比例の式の問題

簡単だよね。
比例の式っていうのは「ｙ＝決まった数×ｘ」になるから、
答えは「ア：ｙ＝２×ｘ」だね。

次の表のｘとｙは比例している。
比例の式で表しなさい。

決まった数を求めるためにｙ÷ｘを計算しよう。

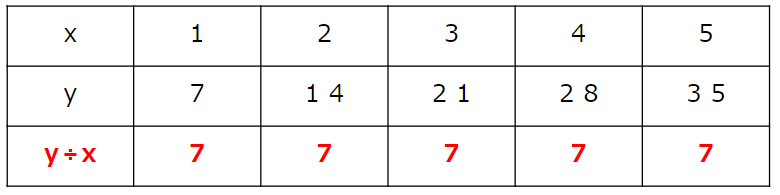
ｙ÷ｘを計算すると、いつも７になることがわかるね。

だから
決まった数は「７」になって、
比例の式は
ｙ＝７×ｘと求まるよ。

次の表のｘとｙは比例している。
比例の式で表しなさい。

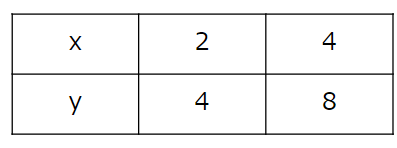
表に書かれている数字や情報が少なすぎて不安に思ってしまうかもしれないね。
これは応用問題だよ。

ただ、やり方はさっきと同じ。
決まった数を求めるためにｙ÷ｘをしよう。

ｙ÷ｘを計算すると、いつも２になることがわかるね。

だから
決まった数は「２」になって、
比例の式は
ｙ＝２×ｘと求まるよ。

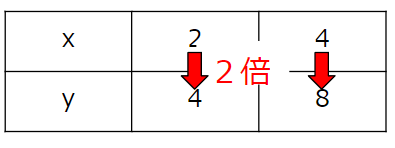
別の考え方

「決まった数」ってどうやって求めるのか忘れちゃった人は
表を縦に見て、
ｘを何倍したらｙになるかを考えよう。

今回の問題ならば、ｘを２倍したらｙになるから
ｙ＝２×ｘ
と比例の式を求めることができるね。

比例の式のまとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。