等しい比の性質とは?比を簡単にする方法(分数の比を整数にする)
小学校6年生の算数で学習する「比」について、等しい比にはどんな性質があるのか、等しい比の性質を使って、数の多い比や小数の比、分数の比を簡単にする方法をわかりやすく解説するよ。
等しい比の性質とは
「比」とは、2つ以上の数字を比べて、どちらのほうが多いかとか、もう片方に比べて何倍か、ということを表すものだったよね。
等しい比とは
次の比をみてみよう。
- 2:3
- 4:6
- 6:9
実はこの3つの比はすべて等しいと言えるんだよ。
それぞれ数字が全然ちがうのに、「等しい」なんて言われても変なかんじだよね。
でも、「比」は2つ以上の数字を比べて、どちらがどのくらい多いかとか、何倍かということをあらわすものだから、それぞれ数字がちがっても、「片方が2倍になっている」という関係性は同じ、ということなんだ。
とはいえ、ぱっと見て「関係性が同じかどうか」って分かりづらいよね。
「2つの数を比べたとき、どちらがどのくらい大きいか」をあらわす便利なものがあったよね。
そう、「比の値」だよ。
さっそくそれぞれの比の値を求めてみよう。
比の値の求め方
a:bの比の値は\(\frac{a}{b}\)とあらわすことができる。
- 2:3だったら、比の値は\(\frac{2}{3}\)
- 4:6だったら、比の値は\(\frac{4}{6}\)
約分すると、\(\frac{2}{3}\) - 6:9だったら、比の値は\(\frac{6}{9}\)
約分すると、\(\frac{2}{3}\)
3つとも、比の値が\(\frac{2}{3}\)だね。
ということは、この3つの「数字の大きさの関係性」は同じということ。
なので、3つの比「2:3」「4:6」「6:9」は等しいといえるよ。
等しい比の性質
等しい比には次の性質があるんだ。
等しい比の性質
- 両方の数に同じ数をかけても等しい
- 両方の数を同じ数でわっても等しい
教科書でも書かれているこの「等しい比の性質」の説明って、ちょっとわかりづらいかもしれないね。
これだと、「等しい比(さっきの2:3と4:6など)には、つぎのような性質がある」というように思ってしまわないかな。
そうすると、等しい比の性質とは「2:3と4:6両方に同じ数をかけても等しい」ということになってしまって、「あれ?よくわからない」となるよね。
これ、ちょっと違うよね。
この「等しい比の性質」という言葉があらわしているのがどういうことか、こまかく説明してみるよ。
さっきの3つの比で考えてみよう。
「両方の数に同じ数をかけても等しい」とは
「両方の数」とは、〇:△の比があったとしたら、この〇と△両方の数ということ。
たとえば2:3なら、両方の数字「2」と「3」に、同じ数をかけるということだよ。
たとえば2をかけてみよう。
2:3は、4:6になるよね。
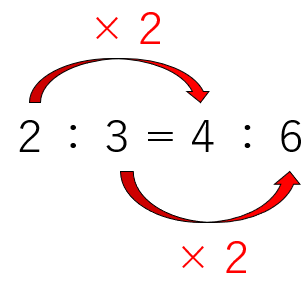
2:3と4:6は、さっき確認したように、比の値が同じだったね。
つまり、等しい比だよね。
等しい比の性質があらわしているのは、
「比の両方の数に同じ数をかけると、かける前の比と、かけた結果できあがる比は等しい比になるよ」
ということなんだね。
「両方の数を同じ数でわっても等しい」とは
これもおなじ。
たとえば6:9の比の両方の数字を3でわると、2:3になるよね。
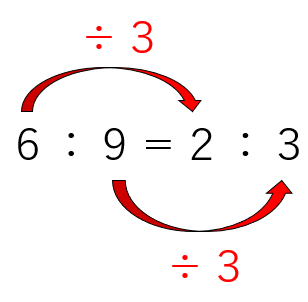
「比の両方の数を同じ数でわると、わる前の比と、わった結果できあがる比は等しい比になるよ」
ということだね。
等しい比の性質についてわかったかな。
- 比の両方の数に同じ数をかけてできる比は等しい比になる
- 比の両方の数を同じ数でわってできる比も等しい比になる
という性質だったね。
なぜこの性質に注目するのかというと、この性質があれば、比の両方の数に同じ数をかけたり、同じ数でわったりしても、等しい比になるからOKだよ!ということになるから。
これのおかげで、数が多い比や、分数の比を簡単にしたいときに、比の両方の数にある数をかけたり、ある数でわったりすることができるんだ。
ではじっさいに、この性質を使って比を簡単にするということをやってみよう。
数の多い比を簡単にする方法
比べるときは、できるだけ「わかりやすい」ほうがいいよね。
だから、「比」は「簡単な比であらわす」ことが必要になったりするんだったね。
30:10を簡単な比にしてみよう。
「比の両方の数を同じ数で割っても比は等しくなる」から
比の両方の数を「10」で割ってみよう。
そうすると3:1になるね。
だから
30:10=3:1
とあらわすことができるんだ。
30:10よりも、3:1のほうが簡単な比でわかりやすいよね。
24:16を簡単な比にしてみよう。
「比の両方の数を同じ数で割っても比は等しくなる」から
比の両方の数を「8」で割ってみよう。
そうすると3:2になるね。
だから
24:16=3:2
とあらわすことができるんだ。
数の多い比を簡単にするポイント
できるだけ簡単な比にするためには、両方の数をある数で割る必要があるね。
「ある数」とはいっても、どんな数でもよいわけではなくて、その比を簡単にすることができる数を見つけることが重要になってくるよ。
その比を簡単にすることができる「ある数」がどうしてもパッと思いつかなかったら、2つの数字の最大公約数を考えてみればいいんだ。
数の多い比を簡単にする方法
- 2つの数字の最大公約数で割る
なぜなら、
「両方の数をわることができる数でなければならない」=公約数
「できるだけ簡単にしたい(これ以上割れないようにしたい)」=最大公約数
だからだね。
小数の比を簡単にする方法
数の大きい比を簡単にする方法は2つの数字の最大公約数で割ればよかったよね。
小数の比の場合は少し違うんだ。
0.4:0.5を簡単にしてみよう。
比が小数だと、わかりにくいよね。
だから整数に直そう。
小数を整数に直すために、比の両方の数を10倍するよ。
(0.4×10):(0.5×10)
=4:5
だから
0.4:0.5=4:5
とあらわすことができるんだ。
すべての式をまとめると下のようになるよ。
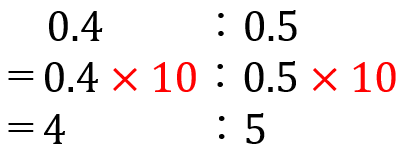
等しい比の性質は
「両方の数に同じ数をかけたり、同じ数でわったりしてもOK」
という性質だったから、比の両方の数に、同じ数である10をかけてもよかったよね。
2.5:4を簡単にしてみよう。
小数を整数に直すために、両方を10倍するよ。
(2.5×10):(4×10)
=25:40
ただ、今回の問題は注意が必要。
これで終わってしまったらだめだよ。だって25:40はまだ簡単な比に直することができるからね。
両方を最大公約数「5」で割ってみよう。
そうすると5:8になるね。
だから
2.5:4=5:8
とあらわすことができるんだ。
すべての式をまとめると下のようになるよ。
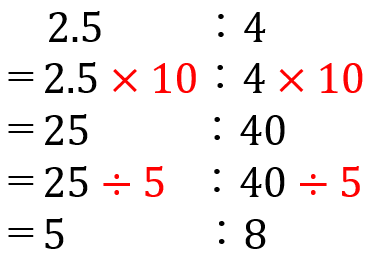
小数の比を簡単にする方法
- 小数を何倍かして整数に直す(両方の数に同じ数をかける)
- 簡単な整数の比にできる場合は、両方の数を最大公約数で割る
分数の比を簡単にする方法
\(\frac{5}{6}\):\(\frac{2}{3}\)を整数の比にしてみよう。
分数の比もわかりにくいよね。だから整数に直すよ。
分数を整数に直す場合は、何倍するかがすごく重要だよ。
ポイントは
分母の最小公倍数をかけること
この問題の分母は
\(\frac{5}{6}\)の6と
\(\frac{2}{3}\)の3
だから最小公倍数は「6」になるよ。
両方を6倍すると、整数になるよ。
(\(\frac{5}{6}\)×6):(\(\frac{2}{3}\)×6)
=5:4
\(\frac{5}{6}\):\(\frac{2}{3}\)=5:4
とあらわすことができるんだ。
分数の比よりも5:4の方がぱっと見わかりやすいよね。
すべての式をまとめると下のようになるよ。
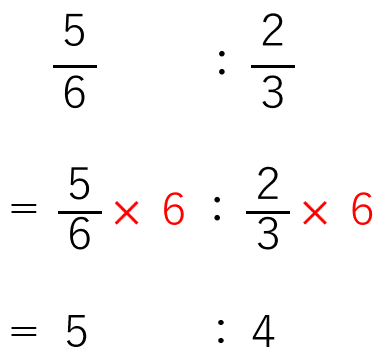
\(\frac{5}{4}\):\(\frac{10}{3}\)を整数の比にしてみよう。
この問題の分母は
\(\frac{5}{4}\)の4と
\(\frac{10}{3}\)の3
だから最小公倍数は「12」になるよ。
両方を12倍すると、整数になるよ。
(\(\frac{5}{4}\)×12):(\(\frac{10}{3}\)×12)
=15:40
ただ、やっぱりここで終わってしまったらだめだよ。
だって15:40もまだ簡単な比に直することができるからね。
両方の数を最大公約数「5」で割ってみよう。
そうすると3:8になるね。
\(\frac{5}{4}\):\(\frac{10}{3}\)=3:8
とあらわすことができるんだ。
分数の比よりも3:8の方がぱっと見わかりやすいよね。
すべての式をまとめると下のようになるよ。
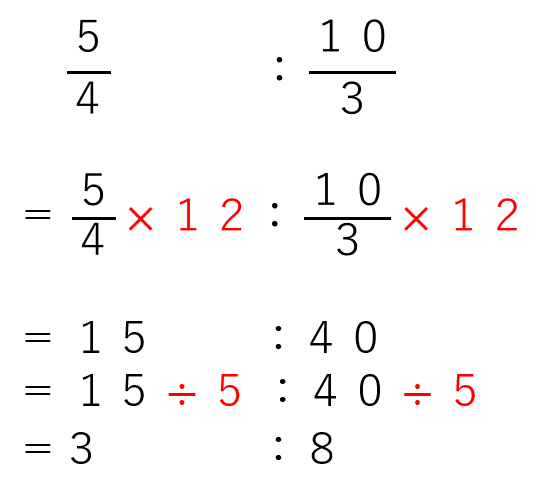
分数の比を簡単にする方法
- 分数を何倍かして整数に直す(分母の最小公倍数をかけるとよい。)
- 簡単な整数の比にできる場合は、両方の数を最大公約数で割る
「等しい比の性質・比を簡単にする方法」まとめ
等しい比の性質
- 両方の数に同じ数をかけても等しい
- 両方の数を同じ数でわっても等しい
数の多い比を簡単にする方法
- 2つの数字の最大公約数で割る
小数の比を簡単にする方法
- 小数を何倍かして整数に直す(両方の数に同じ数をかける)
- 簡単な整数の比にできる場合は、両方の数を最大公約数で割る
分数の比を簡単にする方法
- 分数を何倍かして整数に直す(分母の最小公倍数をかけるとよい。)
- 簡単な整数の比にできる場合は、両方の数を最大公約数で割る
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


