線対称・点対称な四角形の一覧(対称の軸の数)「多角形と対称」
小学校6年生の算数で学習する「多角形と対称」について、これまで学習してきた四角形がそれぞれ線対称か点対称なのかを解説するよ。
また、それぞれの対称の軸の数についても一覧にまとめているよ。
線対称・点対称な四角形の問題もあるので、チャレンジしてみよう!
線対称・点対称な四角形
今まで学習したことがある四角形が線対称か、点対称かを調べてみよう。結論は次のようになっているよ。
- 正方形:線対称かつ点対称になる
- 長方形:線対称かつ点対称になる
- ひし形:線対称かつ点対称になる
- 平行四辺形:点対称になる
- 台形:線対称になることもある
1つずつ順番に詳しく見ていこう。
正方形は線対称かつ点対称になる

正方形は線対称
正方形は下のように折った時に、ピッタリ重なる図形だよね。
だから、正方形は線対称な図形といえるよ。

じゃあ、正方形には「対称の軸」は何本あるか考えてみよう。
もっとわかりやすく言うならば
「折った時にピッタリ重なるようになる折り方は何通りあるか?」ってこと。
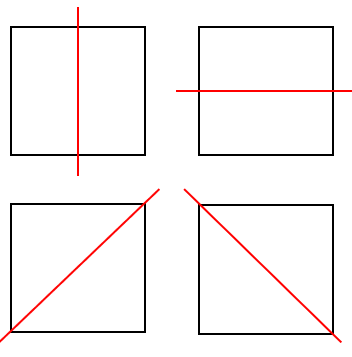
上の図から、ピッタリ重なるような折り方は4通りあることがわかるね。
意外と斜めに折ることを忘れちゃいそうだね。
だから、対称の軸の数は4本ということになるよ。
正方形は点対称
正方形は線対称でもあって、実は点対称でもあるんだよ。
点対称な図形とは、180°回転させたとき、もとの図形にピッタリ重なる図形のこと。
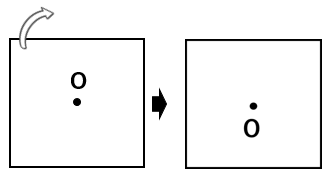
正方形を180°回転させると、ピッタリ重なるよね。
だから、正方形は点対称になるよ。
長方形は線対称かつ点対称になる

長方形は線対称
長方形は下のように折った時に、ピッタリ重なる図形だよね。
だから、長方形は線対称な図形といえるよ。
じゃあ、長方形には「対称の軸」は何本あるか考えてみよう。
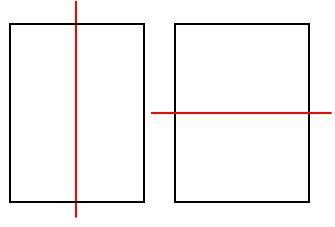
上の図から、ピッタリ重なるような折り方は2通りあることがわかるね。
気をつけなくちゃいけないのが、斜めの場合だよ。
正方形とは違って、斜めで折った時はピッタリ重ならないからね。
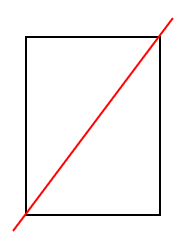
だから、対称の軸の数は2本ということになるよ。
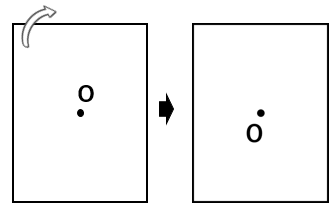
長方形は点対称
長方形は線対称でもあって、実は点対称でもあるんだよ。
長方形を180°回転させると、ピッタリ重なるよね。
ひし形は線対称かつ点対称になる
ひし形は線対称
ひし形は下のように折った時に、ピッタリ重なる図形だよね。
だから、ひし形は線対称な図形といえるよ。
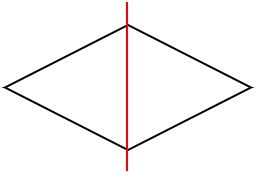
じゃあ、ひし形には「対称の軸」は何本あるか考えてみよう。
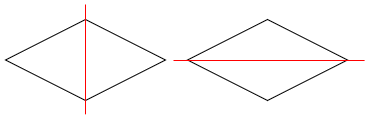
上の図から、ピッタリ重なるような折り方は2通りあることがわかるね。
だから、対称の軸の数は2本ということになるよ。
ひし形は点対称
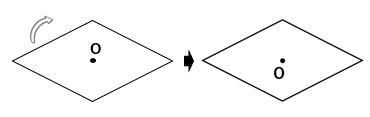
ひし形は線対称でもあって、実は点対称でもあるんだよ。
ひし形を180°回転させると、ピッタリ重なるよね。
平行四辺形は点対称になる
平行四辺形は線対称にならない
平行四辺形はどのように折ってもピッタリ重なることはないよ。
だから、平行四辺形は線対称ではないんだ。
平行四辺形は点対称
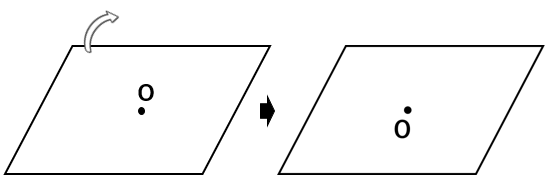
平行四辺形は線対称ではないけど、点対称ではあるんだよ。
平行四辺形を180°回転させたら、ピッタリ重なるよね。
台形は形によって線対称かそうでないかが変わる
台形っていうのは、
下の図のような1組の向かい合う辺が平行な四角形のことだったよね。
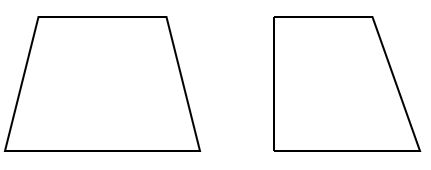
台形は形によって線対称かどうかが変わる性質があるんだ。
線対称になる場合と、ならない場合にわけて考えよう。
線対称になる台形
次のような台形は線対称になるよ。
特徴は台形の脚の部分の長さが等しいってこと。
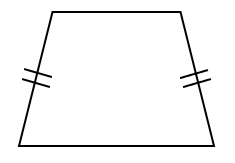
このような台形のことを「等脚台形」って呼ぶよ。
等脚台形は下のように折った時に、ピッタリ重なるよね。
だから、等脚台形は線対称な図形といえるよ。
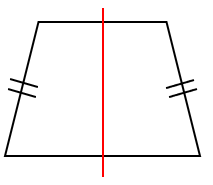
じゃあ、等脚台形には「対称の軸」は何本あるか考えてみよう。
といっても、上のような引き方しか「対称の軸」はないから、
対称の軸は1本ということになるよ。
線対称にならない台形
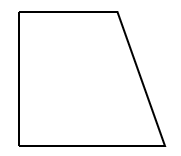
等脚台形(脚の部分の長さが等しい台形)以外は線対称にはならないよ。
上の台形を見てわかると思うけど、
どのように折ってもピッタリ重ならないからね。
台形は点対称にならない
線対称になる台形でも、線対称にならない台形でも、
180°回転させたとき、もとの図形に重ならないよ。
だから、台形は点対称ではないよ。
線対称・点対称な四角形のまとめ
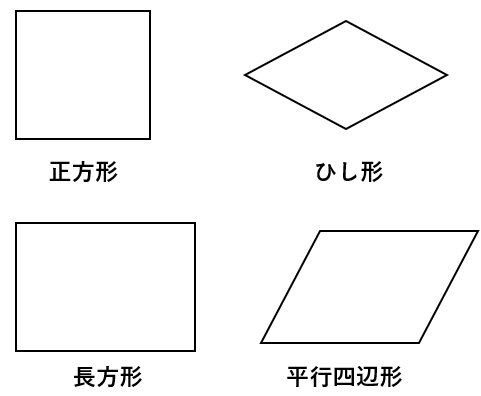
線対称になる四角形や点対称になる四角形を下の表にまとめたよ。
台形だけ形によって、線対称になるかどうかが変わることに注意しよう。
| 四角形 | 線対称 | 対称の軸の数 | 点対称 |
|---|---|---|---|
| 台形 | ✖(〇) | 0(1) | ✖ |
| 平行四辺形 | ✖ | 0 | 〇 |
| ひし形 | 〇 | 2 | 〇 |
| 長方形 | 〇 | 2 | 〇 |
| 正方形 | 〇 | 4 | 〇 |
線対称・点対称な四角形の問題
線対称な図形はどれか。
答え:正方形、長方形、ひし形
折った時に、ピッタリ重なる図形が線対称だったよね。
点対称な図形はどれか。

答え:正方形、長方形、ひし形、平行四辺形
180°回転させたとき、もとの図形に重なるものが点対称だったよね。
対称の軸がもっとも多い図形を選び、対称の軸の本数を答えなさい。

答え:正方形 4本
すべての形の対称の軸を書き入れると次のようになるよ。
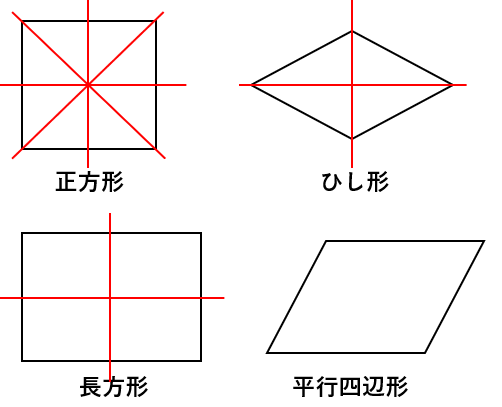
平行四辺形は線対称ではないから、対称の軸が存在しないよ。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


