「並べ方が何通りあるのか」を求める問題の解き方をわかりやすく

小学校６年生の算数で学習する「並べ方が何通りあるのか」を求める問題ではどういうものがあるのか、それぞれの問題のタイプごとに解き方をわかりやすく解説するよ。

数字４桁の並べ方を求める問題、２つの数字を選んで並べ方を求める問題、コインの裏と表の並べ方を求める問題など、解き方を確認しよう。

「並べ方が何通りあるのか」を求める問題の 解き方をわかりやすくのPDF（6枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 数字４桁の並べ方が何通りあるかを求める問題
• ２つの数字を選ぶ並べ方が何通りあるかを求める問題
• コインの裏と表の出方が何通りあるかを求める問題

数字４桁の並べ方が何通りあるかを求める問題

４つの数字から４ケタの整数を作るときの「並べ方が何通りあるか」を求める問題に挑戦してみよう。

問題

１、２、３、４の数字が書かれたカードが１枚ずつあります。
４枚のカードを並べて４ケタの整数を作るとき、何通りの作り方がありますか。

表で考えてみよう。
今回の問題は「４ケタの数字」なので、「千の位」「百の位」「十の位」「一の位」としたらいいね。

数え忘れがないように
千の位の数が「１」の場合だけ考えてみよう。

そうすると、表は次のようになるよ。

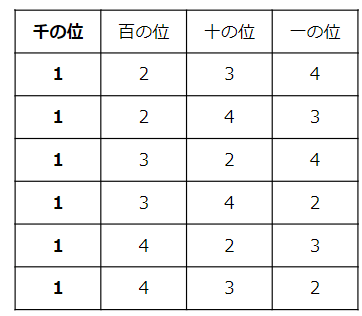
千の位が１のときは全部で６通りの整数ができあがるね。
（１２３４、１２４３、１３２４、１３４２、１４２３、１４３２）

あとは千の位が２、３、４のときも表を書けるんだけれど、千の位が１のときと同じ考え方になるので、書かなくても全部で何通りあるかがわかるよね。

千の位が１のときに６通りの整数ができるので、
千の位が２のときも６通りの整数、
千の位が３のときも６通りの整数、
千の位が４のときも６通りの整数ができるってことだよね。

だから、全部で６通り×４で２４通りの４ケタの整数ができあがるよ。

２つの数字を選ぶ並べ方が何通りあるかを求める問題

それでは、今度は４つの数字の中から２つの数字を選ぶときの並べ方が何通りあるかを求める問題を考えてみよう。

問題

１、２、３、４の数字が書かれたカードが１枚ずつあります。
４枚から２枚選んで２ケタの整数を作るとき、何通りの作り方がありますか。

さっきの問題と違うのは、「４枚から２枚を選ぶこと」だよ。
選んだ２枚で２ケタの整数を作るから「十の位」「一の位」だけを考えればいいね。

数え忘れがないように
十の位の数が「１」の場合だけ考えてみよう。

十の位が１だとしたら、一の位は２、３、４の場合があるので、図にすると次のようになるよ。

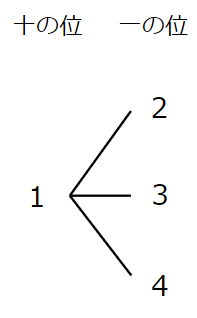
今回の問題は「２ケタ」の数字なので、ここで終わりだよ。
十の位が１のときは全部で３通りの整数ができあがるね。
（１２、１３、１４）

あとは十の位が２、３、４のときも図を書いたらいいんだけれど、
書かなくても全部で何通りあるかがわかるよね。

十の位が１のときに３通りの整数ができるんだから
十の位が２のときも３通りの整数、
十の位が３のときも３通りの整数、
十の位が４のときも３通りの整数ができるってことだよね。

だから、全部で３通り×４で１２通りの２ケタの整数ができあがるよ。

一応すべての図を書いておくと次のようになるよ。
やっぱり１２通りあることがわかるね。

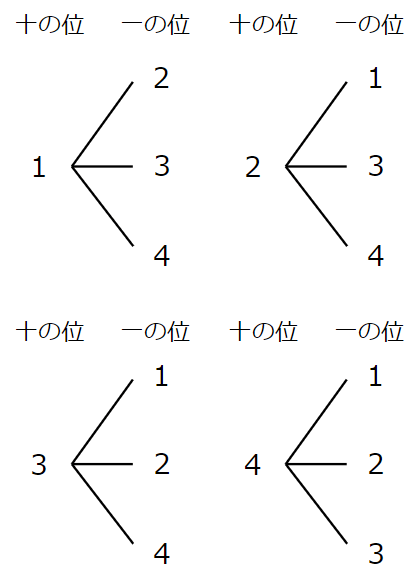
コインの裏と表の出方が何通りあるかを求める問題

それでは今度はコインを投げたときに、おもてとウラがどのように出るかを、並べ方が何通りあるかを求めることで考える問題を紹介するよ。

問題

１０円玉を３回投げます。おもてとウラの出方は全部で何通りありますか。

この問題も並び方なの？と思うかもしれないけれど「おもてとウラの並び方」の問題なんだ。
おもてを〇、ウラを✖にして、図（樹形図）で考えてみよう。

まず
１回めがおもてだった場合を考えよう。

１回め投げて「おもて」だったら、２回め投げたら「おもて」か「ウラ」のどちらかだよね。

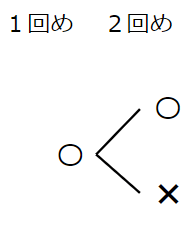
１回めが「おもて」、２回めも「おもて」だった場合、３回め投げたら「おもて」か「ウラ」のどちらかだよね。

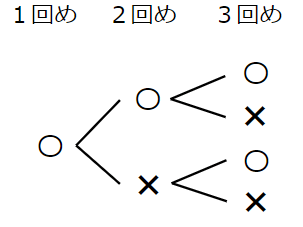
１回めが「おもて」だった場合、「おもて」「ウラ」の出方は４通りとわかるよ。

次に
１回めがウラだった場合を考えよう。

１回めが「ウラ」だった場合の図は次のようになるよ。

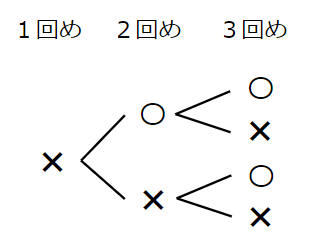
１回めが「ウラ」だった場合も、「おもて」「ウラ」の出方は４通りとわかるよ。

まとめると次のようになるよ。

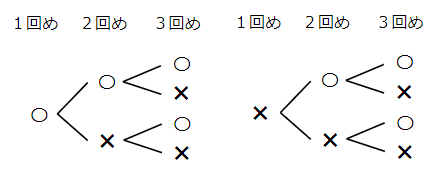
「おもて」「ウラ」の出方は全部で８通りあることがわかったね。

８通りがそれぞれどういう出方かをまとめておくよ。

問題のタイプによって、表と図をうまく使って解けるようにしよう。
できるだけたくさんのタイプの問題に挑戦しておくことで、だんだんコツがつかめてくるよ。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。