「並べ方が何通りあるのか」の求め方を解説(表と図での表し方)
小学校6年生の算数で学習する「並べ方」について、並べ方が何通りあるのかを求める方法をわかりやすく解説するよ。
「表」を使って並べ方が何通りあるかを求める方法、「図」を使って並べ方が何通りあるかを求める方法、それぞれのやり方をくわしく紹介していくよ。
並べ方を表で表して調べてみよう
次のような並べ方を考えてみよう。
けんた、まさる、はると、しずかの4人でリレーを行います。
1人1回ずつ走るとすると、走る順番は何通りありますか。
「順番」という単語を問題文で見つけたら、「並べ方を考えればいいんだな」と思ってOK。
「走る順番が何通りあるかを求める問題」はよくテストでも出てくるし、中学生になっても勉強する内容なので、しっかりできるようにしておこう。
運動会でのリレーの順番決めでも役立つと思うよ。
走る順番を考えるには、表にして考えるとわかりやすいよ。
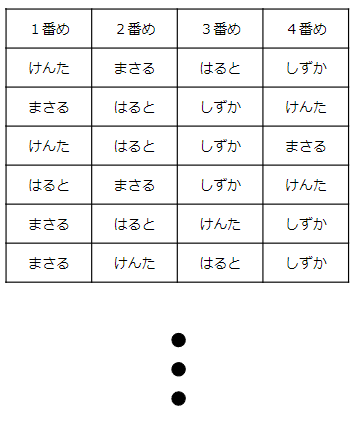
ただ、いざ書いてみると「めんどうくさいな」と思うかもしれないね。
たとえば、何度も人の名前を書くのは大変だよね。
そういうときは、
けんた=ア、まさる=イ、はると=ウ、しずか=エ
みたいにするのがおすすめ。
そうすると、さっきの表は次のようになるね。
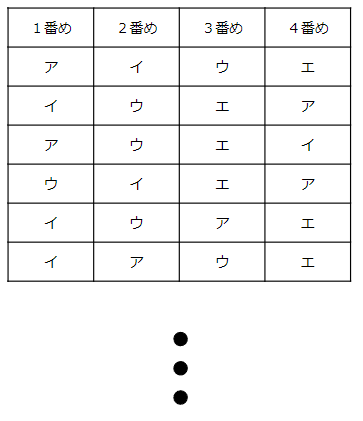
これで「書きやすく」はなったけれど、「走る順番」は上の表に書いてあるもの以外にもまだたくさんありそうだね。
このまま表を書き進めても
「あれ、さっきと同じ順番を書いちゃった」
「しまった、この順番書き忘れていたよ」
「この順番、さっき書いたっけ?」となりそうだね。
並べ方(順番)の問題を解くポイントは「数え忘れがないようにする」ことなんだ。
並べ方を「規則ただしく」表で書く方法
数え忘れがないようにするためには、「規則ただしく」書く事が大事。
どうやって「規則ただしく」書くかを説明するよ。
まず、
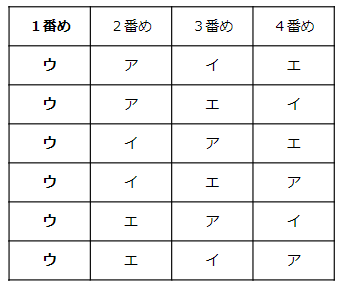
1番めの人が「けんた=ア」の場合だけを考えてみよう。
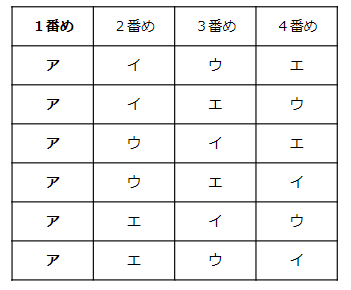
このとき、上の表のように2番目も「イ」からはじめて、次に「ウ」、その次に「エ」を並べていくようにしよう。
わからなかったら読もう!
「ア・イ・ウ・エ」の並べ方のくわしい流れを説明するよ。
➀まずは1列目を「ア」からはじめる。
➁1列目の次は順番通り「イ」にする。
③1列目のさらに次も順番通り「ウ」にする。
④1列目のさらに次も順番通り「エ」にする。
⑤2列目にいく。「ア」から始める。
⑥2列目の次は順番通り「イ」にする。
⑦2列目のさらに次は、順番では「ウ」だけれど、それだと1列目とおなじ並び方になってしまうので、「エ」を先にもってくる。
⑧2列目のさらに次は、残っている「ウ」にする。
⑨3列目にいく。「ア」から始める。
⑩3列目の次は順番通りであれば「イ」だけれど、それだと1列目か2列目と同じ並び方になってしまうので、「ウ」を先にもってくる。
⑪3列目のさらに次は⑩で順番を抜かした「イ」をもってくる。
⑫3列目のさらに次は、残っている「エ」にする。
⑬4列目に行く。「ア」から始める。
⑭4列目の次は順番通りであれば「イ」だけれど、それだとやっぱり1列目か2列目と同じ並び方になってしまうので、「ウ」を先にもってくる。
⑮4列目のさらに次は⑭で順番を抜かした「イ」をもってきたいけれど、それだと3列目と同じ並び方になってしまうので、先に「エ」をもってくる。
⑯4列目のさらに次は、残っている「イ」にする。
このような考え方で、「すでに出てきた並び方にならないように」しながら、「ア・イ・ウ・エ」の順番を守ることで、規則正しく並べることができるよ。
1番めの人が「けんた=ア」の場合だけを全て書き終えたら、こんどは
1番めの人が「まさる=イ」の場合だけを考えてみよう。
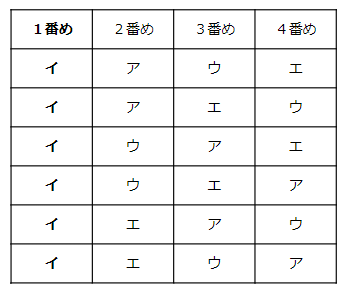
次に
1番めの人が「はると=ウ」の場合だけを考えてみよう。
最後
1番めの人が「しずか=エ」の場合だけを考えてみよう。
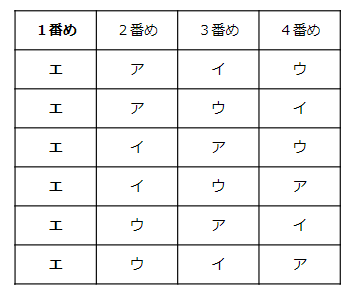
まとめると次のようになるよ。
- 1番めの人が「けんた=ア」の場合 6通り
- 1番めの人が「まさる=イ」の場合 6通り
- 1番めの人が「はると=ウ」の場合 6通り
- 1番めの人が「しずか=エ」の場合 6通り
走る順番は全部で6通り×4で、24通りあるってことがわかったね。
こうやって、1番めの人を決めてから、そろえて考えると数え忘れが起きにくいんだ。
並べ方(順番)を表で表すときのポイント
- 数え忘れがないように、1番めをそろえて考えるといい。
並べ方を図で表して調べてみよう
さっきと同じ問題を図で表して調べてみよう。
もちろん表で考えてもいいんだけれど、中学生になると図で考えることが多くなるから、今のうちにマスターしておこう。
けんた、まさる、はると、しずかの4人でリレーを行います。
1人1回ずつ走るとすると、走る順番は何通りありますか。
並べ方(順番)の問題を解くポイントは「数え忘れがないようにすること」だったよね。
数え忘れがないように、さっきは表で考えたけど、今度は図で考えるよ。
数え忘れがないようにするために
1番めの人が「けんた=ア」の場合だけ考えてみよう。
1番めが「ア」だったら、2番めは「イ」「ウ」「エ」のどれかだよね。
だから、次のように表すよ。
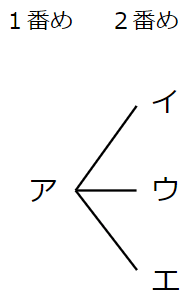
1番めが「ア」で、2番めが「イ」だったら、
3番め、4番めは「ウ」「エ」か「エ」「ウ」になるよね。
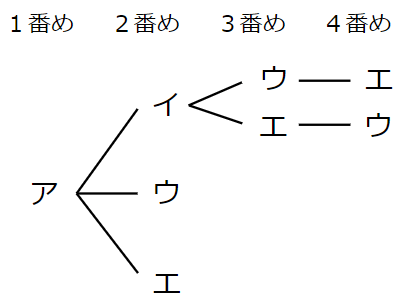
同じように
1番めが「ア」、2番めが「ウ」
1番めが「ア」、2番めが「エ」
の続きを書くと次のようになるよ。
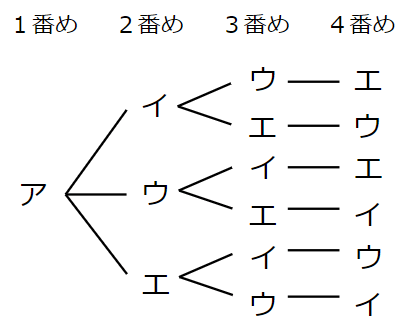
次に
1番めの人が「まさる=イ」の場合だけ考えてみよう。
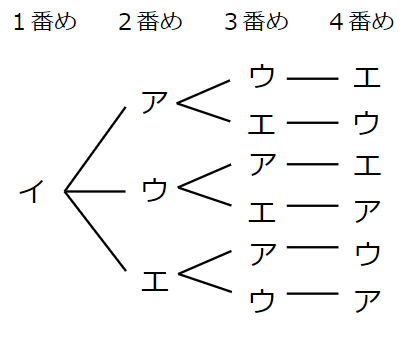
次に
1番めの人が「はると=ウ」の場合だけ考えてみよう。
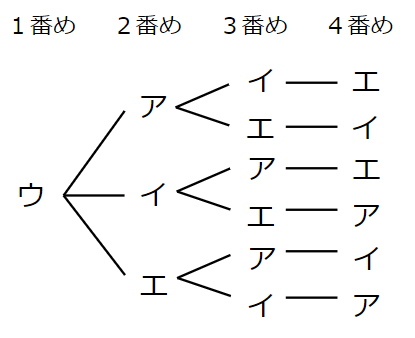
最後に
1番めの人が「しずか=エ」の場合だけ考えてみよう。
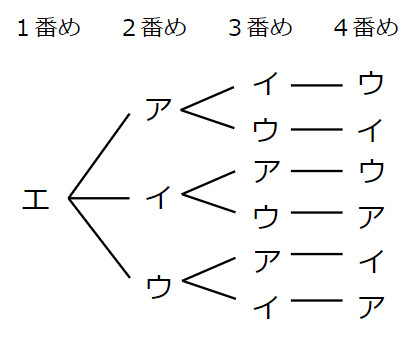
まとめると次のようになるよ。
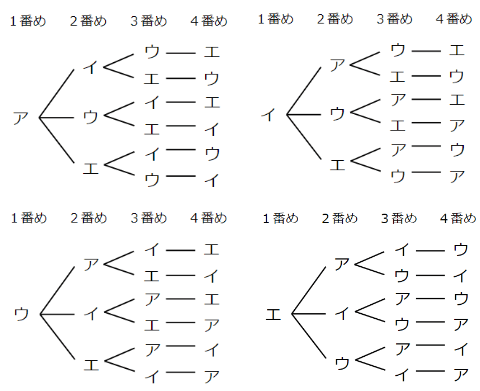
図を見てもわかるけど、
走る順番は6通り×4で、24通りあることがわかるね。
いちいち、すべての場合を書かなくても、1番めが「けんた=ア」の場合だけ書くことができたら、あとは同じ考え方だから、全部で何通りあるかは求められそうだよね。
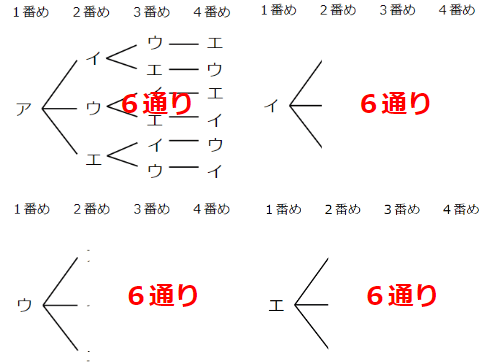
こういう図のことを「樹形図」っていうよ。
(樹形図という言葉は中学校で登場するよ)
「樹」という漢字は、「樹木」という単語からわかるように、「木」のことだよ。
まさにさっきの図は、木のようにどんどん枝分かれしていっているよね。
まるで木のような図だから、「樹形図」と呼ぶんだ。
「並べ方が何通りあるかを求める」まとめ
「並べ方」が何通りあるかを求める方法 まとめ
- 並べ方を考えるときは表や図で表して考えるとよい。
- 数え忘れがないようにすることが重要。
- 1番めをそろえると、数え忘れが起きにくい。
- すべての表や図を書かなくても、1番めが〇〇の場合さえ数えることができれば、すべての場合が計算できる。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


