平均値・最頻値・ドットプロットとは？求め方と表し方を簡単に解説

小学校６年生の算数で学習する「平均値」「最頻値（モード）」「ドットプロット」について、平均値と最頻値とはどういう意味か、ドットプロットはどんな意味かを簡単に紹介するよ。

平均値・最頻値の求め方、ドットプロットを使ってデータのちらばりを表す方法を練習問題も使って解説するよ。

平均値・最頻値・ドットプロットとは？ 求め方と表し方を簡単に解説のPDF（11枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 平均値とは？平均値の求め方
• ドットプロットで表してみよう
• 最頻値（モード）とは
• まとめ

平均値とは？平均値の求め方

小学５年生でも「平均」について勉強したね。
かんたんに復習をしてみよう。

小学６年生の算数では「平均値」という言葉になって出てくるんだけれど、内容は５年生で学習した「平均」と同じことだと思って大丈夫だよ。

平均値を求めてみよう

平均の求め方は、「平均＝合計÷個数」の計算で求めることができるよね。
では、実際に例題をときながら平均値の求め方を確認してみよう。

次の結果は、１組と２組のハンドボール投げの結果です。
平均値を求めましょう。

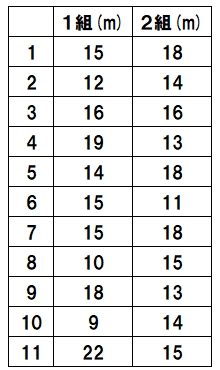
※左に書いてある１～１１は出席番号だよ。
１組の５番の人は１４ｍ、２組の７番の人は１８ｍ投げたということだね。

平均値の求め方は、平均と同じで「合計÷個数」をすればよかったね。
ただ、この問題は「１１人」の生徒だから、「個数」ではなくて「人数」になるので「合計÷人数」になるね。

まず、１組と２組それぞれの、１１人全員の「投げた距離」の合計を求めよう。

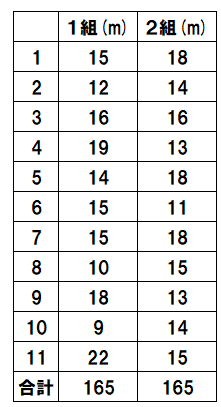
１組の結果をすべて足すと１６５ｍ、
２組の結果をすべて足すと１６５ｍ。

だから１組の平均値は「合計÷人数」で、
１６５÷１１＝１５ｍ
と求めることができるね。

２組の平均値も「合計÷人数」で、
１６５÷１１＝１５ｍ
と求めることができるね。

データを平均値で比べよう

「平均値」がわかると、データを比べたりするときに便利なんだ。
たとえば、ハンドボール投げの結果をもう一度見てみよう。

ぱっと見て、１組と２組のどちらが遠くまで投げているかを判断するのは難しいよね。

「１組だな。だって２２ｍも投げた人がいるもん」
「２組でしょ。だって、２組はみんな１１ｍ以上だよ。１組は９ｍの人もいるじゃん」
なんて、いろんな声が出てきそうだよね。

このように、データは「何に注目するか」によって「どっちが遠くまで投げているか」の判断が変わってくるんだ。

「一番遠くまで投げた」ことに注目すれば１組だし、
「みんなが１１ｍ以上だった」ことに注目すれば２組になるということだね。

でもこれって、たまたますごく遠くまで投げられた人がいたり、逆にすごく遠くまで投げられた人がいたのに、何人かが１１ｍ未満だったら負けてしまったり、少し不公平にも感じるね。

それに対して、「平均値」は、生徒ごとにバラバラな記録をならして、公平に比べることができるんだ。

平均値に注目すると、どちらも「１５ｍ」で同じだったから、１組も２組は同じくらい遠くに投げたというのが答えになるね。

データをドットプロットで表してみよう

「ドットプロット」というのは、数直線上に点（ドット）を打つ（プロット）データの表し方のことだよ。

さっきのハンドボール投げの１組の結果をドットプロットで表すと下のようになるよ。
「９ｍ投げた人」を表すには、数直線の「９」のところにひとつ点を打てばいいんだね。
「１５ｍ投げた人が３人」だったら、「１５」のところに３つ点を打てばいいね。

ドットプロットに表すと、次のようなことがひと目でわかるよ。

同じように２組の結果もドットプロットで表してみよう。

ドットプロットに表すと、次のようなことがひと目でわかるよ。

ドットプロットで比較する

ドットプロットで表すと、ひと目でデータとデータの違いを比べやすくなるよ。

さっそく、１組と２組のドットプロットを並べてみよう。
ドットプロットで表すと、データの散らばりぐあいがわかりやすくなるんだ。

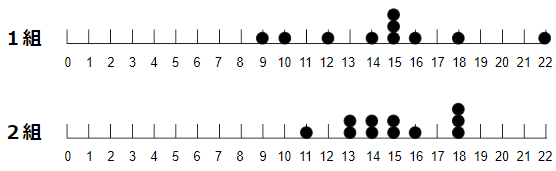
ドットプロットで比べると、次のような違いがひと目でわかるね。

最頻値（モード）とは

最頻値さいひんちという言葉だけだと、なんだか難しそうだよね。
でも、漢字を見ると

「最」・・・最も
「頻」・・・頻度ひんどが高い＝多く出る
「値」・・・あたい

つまり、「最も多く出る値」のことなんだ。

最頻値のことは英語で「モード」というよ。
みんなはあまり聞いたことがないかもしれないけど、流行している用服のことを「モード」と言ったりするんだ。
流行しているということは、「多くの人が着ている」ということだよね。
そこからも、「モード」＝「最頻値」とつなげて覚えられるよ。

話は戻って、最頻値は「最も多く出る値」のことだったね。
例えば、さっきのハンドボール投げの１組の結果だったら、「最も多く出ている値」は３回登場する「１５」だね。

なので、１組の最頻値は１５ｍだとわかるね。

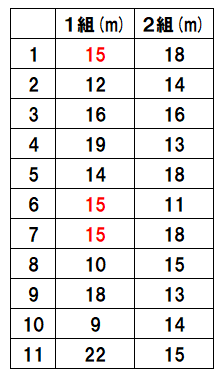
ドットプロットからも最頻値を求めることができるよ。

プロットが３つ打たれている「１５」が最頻値だとすぐにわかるね。
表よりもドットプロットの方が最頻値はわかりやすいかもしれないね。

ただ、ドットプロットを見ると、次のように間違えてしまう可能性があるから気をつけよう。

２組の最頻値も求めてみよう。

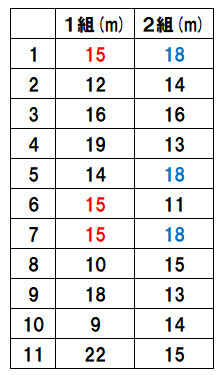
表を見ると、３回登場している「１８」が最頻値だね。
ドットプロットを見ても、ドットが３つ打たれている「１８」が最頻値で間違いないね。

２組の最頻値は、１８ｍだとわかるね。

データを最頻値で比べよう

１組の最頻値は１５ｍ、２組の最頻値は１８ｍだから、
最頻値で比べると２組の方が遠くまで投げていることがわかるね。

平均値で比べたときは１組と２組は同じだったけれど、最頻値で比べると変わってくるね。

このように、データは「何に注目するか」で判断が変わってくるんだね。

平均値と最頻値を求める問題

クラスで大縄跳びを１０回挑戦しました。
このときの記録の、平均値と最頻値を求めなさい。

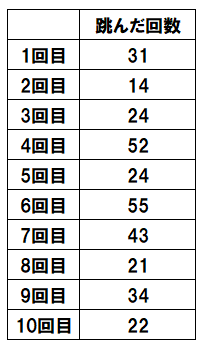
平均値を求めよう

平均値は
「合計÷個数（回数）」で求まるから、
１～１０回目までの跳んだ回数を合計しよう。

３１＋１４＋２４＋５２＋２４＋５５＋４３＋２１＋３４＋２２＝３２０

と計算できるよ。

飛んだ回数の合計３２０を、挑戦した回数１０で割ると

３２０÷１０＝３２回

と求めることができるね。
平均値は、３２回だね。

最頻値を求めよう

最頻値は最も多く出ている値のことだから、２回登場している「２４」だと求めることができるね。

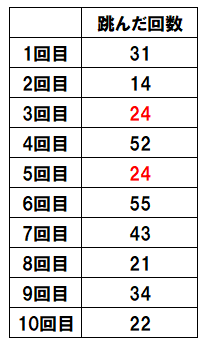
最頻値は、２４回だね。

平均値・最頻値・ドットプロット　まとめ

６年生ではこの後、「中央値」というのも勉強するから、まずは平均値や最頻値をマスターしておこうね。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。