「線対称な図形」とは?性質と対象の軸・問題の解き方を確認しよう
小学校6年生の算数で学習する「線対称な図形」について、線対称な図形とはどんな図形なのか、対象の軸とはなにか、線対称な図形の性質や、問題の解き方をわかりやすく解説するよ。
線対称な図形とは
今までいろいろな図形を勉強してきたね。
今回は「線対称な図形」について学んでいくよ。
線対称な図形とは、ある線で折った時に、ピッタリ重なる図形のことだよ。
線で折った時ときに重なるから「線」対称という名前がついているよ。
次のような図形が線対称になるよ。
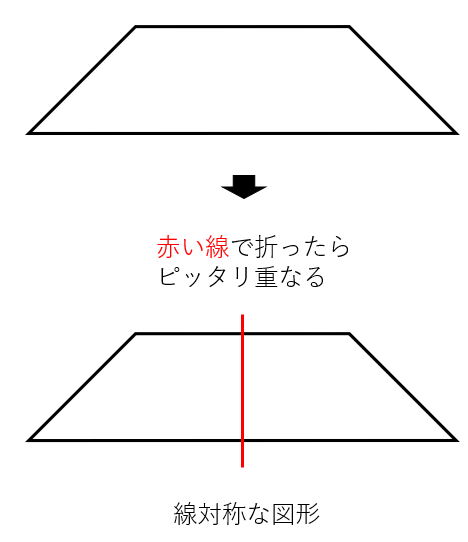
確かに、上の赤い線で折った時にピッタリ重なることがわかるね。
教科書では、線対称な図形とは
「1つの直線を折り目にして二つ折りにしたとき、両側の部分がピッタリ重なる図形」と書いてあるよ。
なんとなくわかったかな?
では、どんな図形が線対称で、どんな図形が線対称ではないかを紹介するね。
線対称な図形の例の一覧
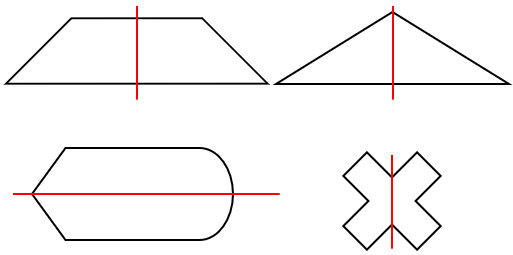
→赤い線で折ったらピッタリ重なるね。
線対称ではない図形
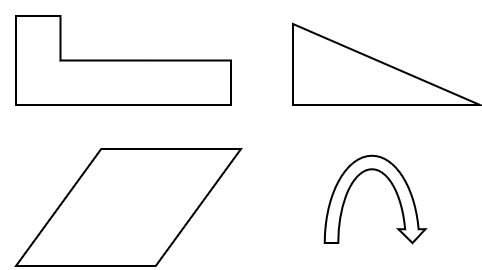
→どう折ってもピッタリ重なることはないね。
「線対称な図形」と「線対称ではない図形」の違いがわかったかな?
ある直線で折った時にピッタリ重なる図形が線対称だと覚えておこうね。
対称の軸とは
「線対称な図形」の学習で登場する大事な言葉が「対称の軸」。
線対称な図形と対称の軸という言葉はセットで出てくるから必ず覚えておこう。
線対称な図形とは、ある直線で折った時にピッタリ重なる図形だと説明したよね。
その「ある直線(真ん中の線)」を、対象の軸と呼ぶんだ。
もっとわかりやすくいってしまえば
「ピッタリ重なるように折った時の折り目」だとイメージすればOKだよ。
たとえば下のような線対称な図形だったら、赤い線が「対称の軸」になるよ。
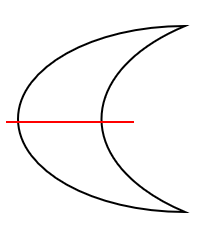
対応する辺の長さと対応する角の大きさの性質
それでは、線対称な図形にはどんな性質・特徴があるのか確認していくよ。
線対称な図形とは、ある直線で折った時にピッタリ重なる図形のことだったよね。
今から、「当たり前だよ!」ってツッコミを入れたくなるようなことを紹介するね。
下の図を見てみよう。
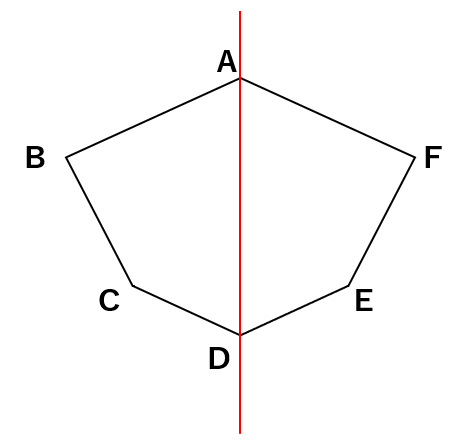
- 角Bと重なるのは角Fだから、角Bと角Fの大きさは等しい
- 角Cと重なるのは角Eだから、角Cと角Eの大きさは等しい
- 辺ABと重なるのは辺AFだから、辺ABと辺AFの長さは等しい
AB=AF - 辺BCと重なるのは辺FEだから、辺BCと辺FEの長さは等しい
BC=FE - 辺CDと重なるのは辺EDだから、辺CDと辺EDの長さは等しい
CD=ED - 左と右の図形はピッタリ重なるから合同である
線対称な図形は、対称な軸で折ったときにピッタリ重なる図形なんだから、上の6つのことは、当たり前のことだよね。
ここで3つの言葉を紹介するね。同じ色の点や辺や角に注目しよう。
対応する点
「対応する点」とは、線対称な図形を二つ折りにしたときに、重なり合う点のことだよ。
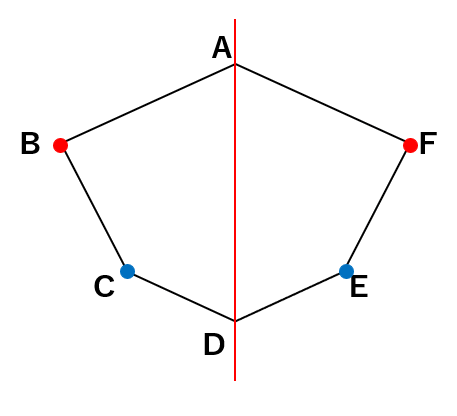
たとえば点Bの対応する点が点F、点Fにとっての対応する点も点Bということだね。
対応する辺
「対応する辺」とは、線対称な図形を二つ折りにしたときに、重なり合う辺のことだよ。
なので、対応する辺は、長さが等しくなるよ。
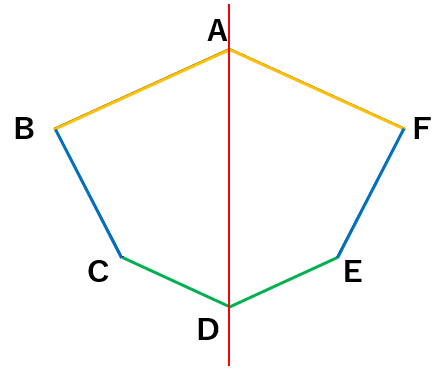
たとえば辺ABの対応する辺は辺AF。辺AFにとっての対応する辺も辺ABだね。
そして、辺ABと辺AFの長さは等しくなるよ。
対応する角
「対応する角」とは、線対称な図形を二つ折りにしたときに、重なり合う角のことだよ。
なので、対応する角は、角の大きさが等しくなるよ。
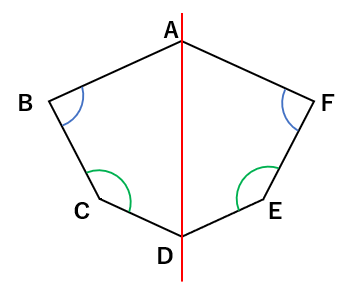
たとえば、角Bの対応する角は、角Fだね。そして角Fにとっての対応する角は角Bだよ。
そして角Bと角Fは大きさが等しくなるね。
「対応する〇〇」とは、5年生で学習した「合同な図形」でも学習したから大丈夫だったと思うけれど、対応する点や辺や角についてわかったかな?
線対称な図形の性質についてまとめよう。
線対称な図形の性質
線対称な図形では、対応する辺の長さや角の大きさは等しくなる。
線対称な図形の辺の長さや角度を求める問題
それでは線対称な図形の性質を使って、次の問題に挑戦してみよう。
例題
次の三角形は線対称な図形です。
辺ACの長さと角Cの大きさを求めましょう。
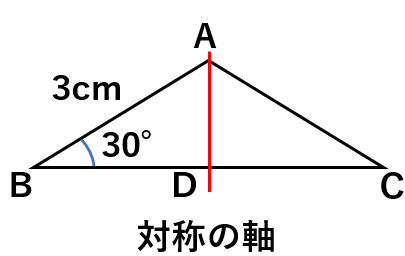
図形を二つ折りにしたときに、辺ACと重なる辺(対応する辺)は辺ABだね。
辺ABは3cmで、対応する辺の長さは等しくなるので、辺ACもおなじ3cmになるよ。
図形を二つ折りにしたとき、角Cと重なる角(対応する角)は角Bだね。
角Bは30°なので、角Cもおなじ30°になるよ。
線対称な図形の性質をもう一度確認しよう。
線対称な図形の辺や角が等しくなる性質は、すごく重要なので、必ず覚えておこう。
もうひとつ、線対称な図形の重要な性質を紹介するよ。
線対称な図形と対象の軸の性質
線対称な図形と対称の軸の関係について考えてみよう。
まず、対応する点同士(青い線・緑の線)を結んでみよう。
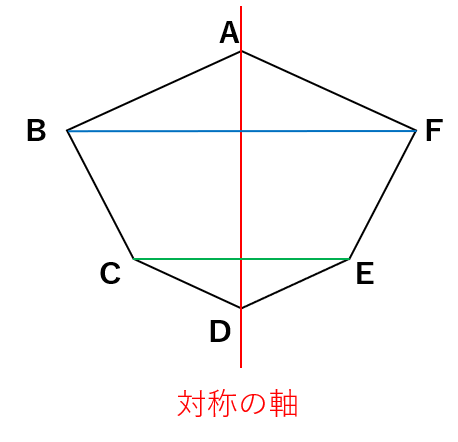
「対応する点同士を結んだ線(青い線・緑の線)」と対称の軸は、垂直に交わるんだ。
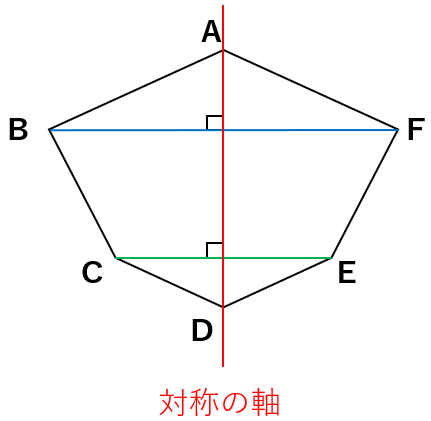
「対応する点同士を結んだ線(青い線・緑の線)」と対称の軸が交わっているところを、上から点G、点Hとすると、
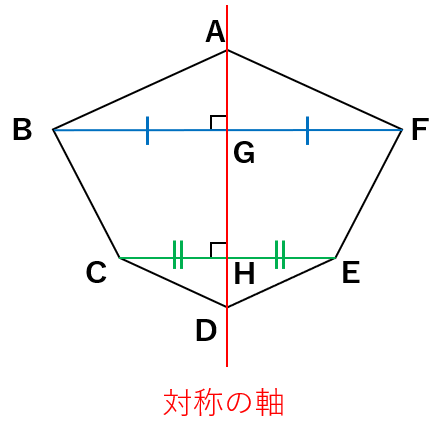
BG=FG、CH=EHになるよね。
これらの線対称な図形と対称の軸の関係についてまとめると次のようになるよ。
線対称な図形と対称の軸の関係
- 線対称な図形では、対応する「2つの点を結ぶ直線(青い線・緑の線)」は、対称の軸と垂直に交わる。
- 交わる点(点G・点H)から対応する2つの点までの長さは等しくなる。

線対称な図形と対称の軸の関係を使った問題
それでは、さっそく「線対称な図形と対象の軸の関係」を使った問題に挑戦してみよう。
例題
次の図形は線対称な図形で、赤い線は対称の軸、青い線は対応する点同士を結んだ線です。
DKの長さが2cmのとき、HKの長さは何cmですか。
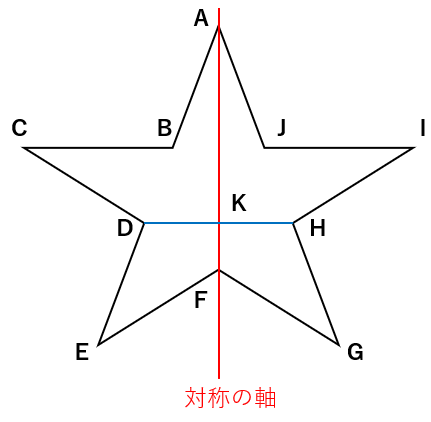
線対称な図形では、「対応する2つの点を結ぶ直線(青い線)」と「対称の軸(赤い線)」が交わる点から対応する2つの点までの長さは等しくなるという性質があったよね。
だから、DK=HKになるよ。
なので、HKの長さはDKと同じ2cmだよ。
「線対称な図形の性質」まとめ
- 1つの直線を折り目にして二つ折りにしたとき、両側の部分がピッタリ重なる図形のことを「線対称な図形」という
- 1つの直線を折り目にして二つ折りにしたとき、両側の部分がピッタリ重なり線対称な図形になる場合、その1つの直線のことを、「対象の軸」という
- 線対称な図形では、対応する辺の長さや角の大きさは等しくなる
- 線対称な図形の対応する点同士を結んだ線と対称の軸は、垂直に交わる
- 線対称な図形の対応する点同士を結んだ線と、対称の軸が交わる点から対応する2つの点までの長さは等しくなる
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


めちゃくちゃ分かりやすかったです。