「反比例のグラフ」書き方と比例との違い・特徴をわかりやすく解説
小学校6年生の算数で学習する「反比例のグラフ」について、反比例のグラフの書き方と特徴、比例のグラフとはどう違うのか、反比例のグラフを書くときの注意点などをわかりやすく解説するよ。
反比例の関係をグラフに表してみよう
今まで反比例の性質や反比例の式について勉強してきたよね。
今回は反比例の関係を「グラフ」で表わすにはどうすればいいかを学習するよ。
反比例の関係にある2つ以上の数量をグラフに表そう①
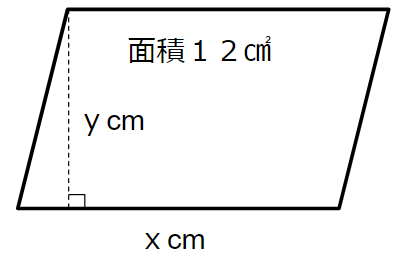
例えば、次のような面積が12cm平行四辺形の
「底辺xcm」と「高さycm」は反比例の関係にあるんだったよね。
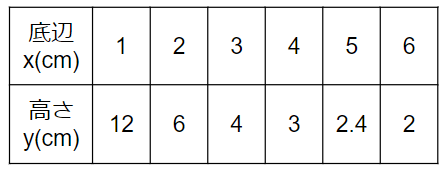
だって、xが2倍、3倍、4倍・・・になると、
yは\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍、\(\frac{1}{4}\)倍・・・になっているからね。
まさに反比例の性質だね。
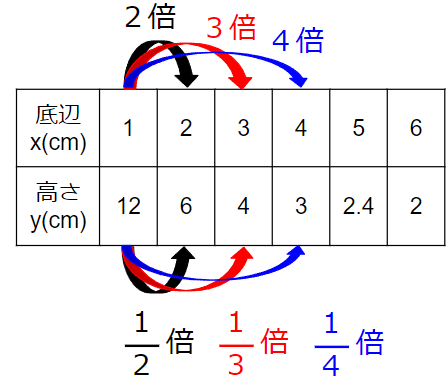
この表を使ってxとyの関係をグラフに表していこう。
比例の関係をグラフに表すときと同じように
反比例の関係をグラフに表すには次の2ステップが大切だよ。
反比例の関係をグラフに表す2ステップ
- xとyの値の点をとる
- すべての点を通るようになめらかな曲線で結ぶ
「曲線」っていうのは曲がった線のことだよ。
なぜ曲線になるのか、実際に書いて確認しよう。
xとyの値の点をとる
さっきの表はxが6のときまでしかなかったけれど、xが12のときまで考えてみよう。
xが7~12を書いてみたよ。
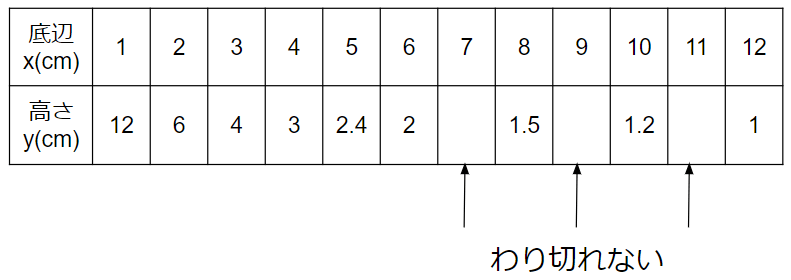
ただxが7のときと、9のときと、11のときはyの値が割り切れないから、今回は無視して下のような表を考えるよ。
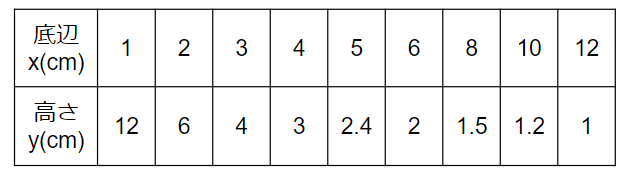
表を縦に見ると、x=1のときy=12だよね。
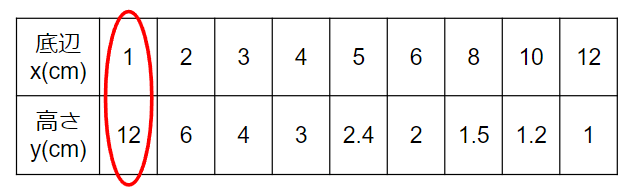
あとは他の点も順番に考えていったらOK。
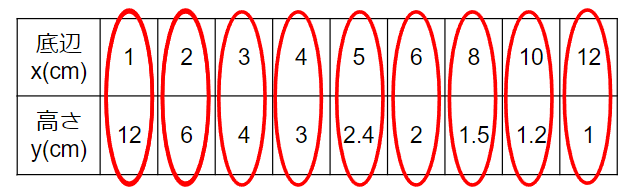
①x=1のとき、y=12
横軸が1で縦軸が12のところに点を取ろう。
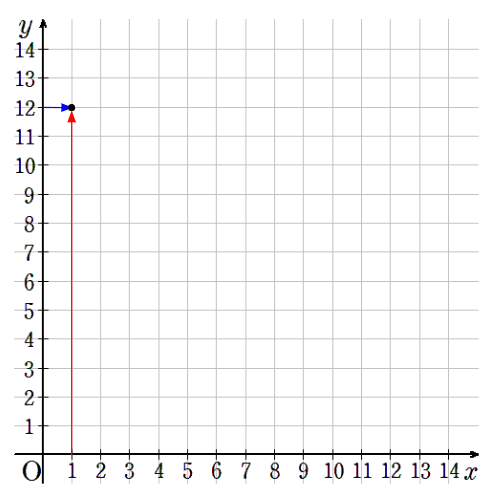
②x=2のとき、y=6
横軸が2で縦軸が6のところに点を取ろう。
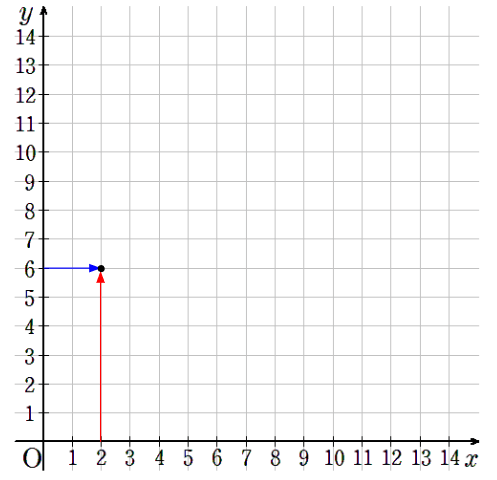
③x=3のとき、y=4
横軸が3で縦軸が4のところに点を取ろう。
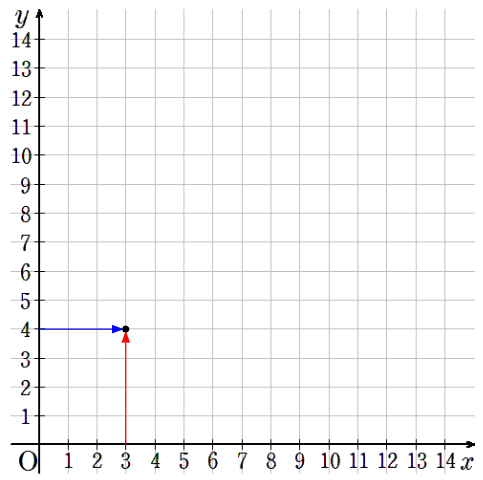
④x=4のとき、y=3
横軸が4で縦軸が3のところに点を取ろう。
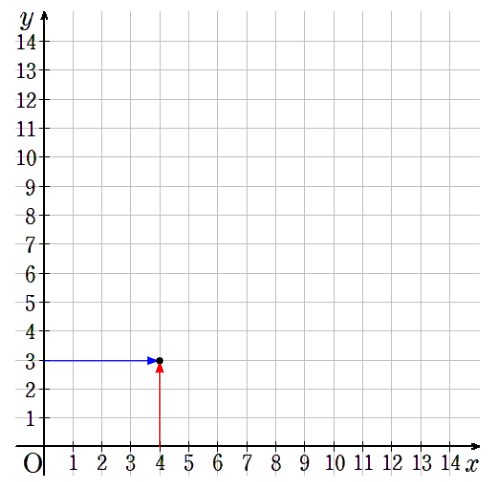
⑤x=5のとき、y=2.4
横軸が5で縦軸が2.4のところに点を取ろう。
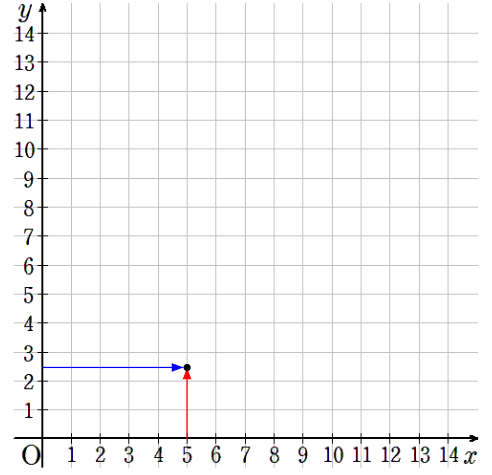
⑥x=6のとき、y=2
横軸が6で縦軸が2のところに点を取ろう。
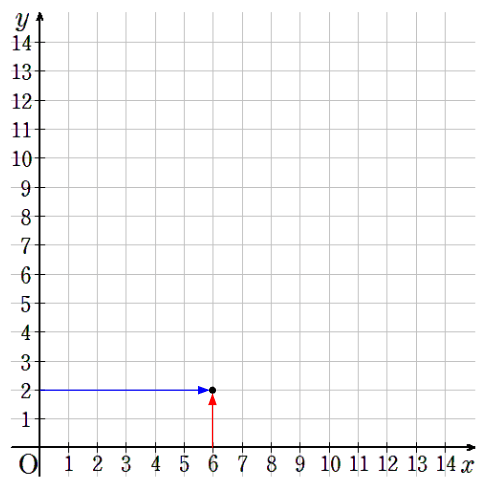
⑦x=8のとき、y=1.5
横軸が8で縦軸が1.5のところに点を取ろう。
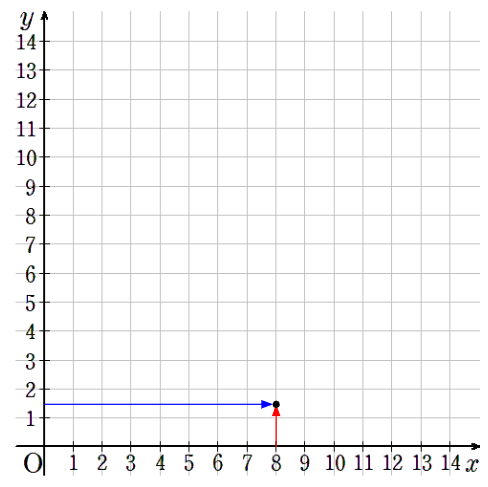
⑧x=10のとき、y=1.2
横軸が10で縦軸が1.2のところに点を取ろう。
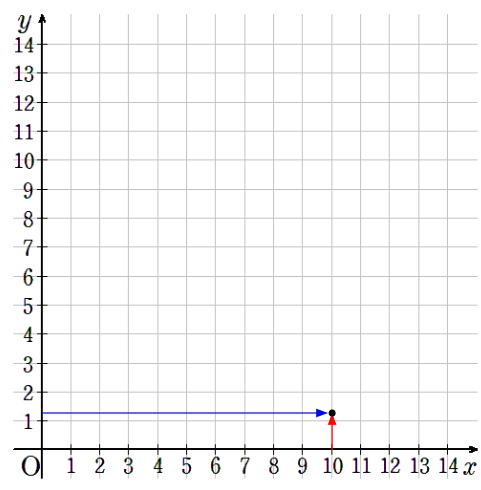
⑨x=12のとき、y=1
横軸が12で縦軸が1のところに点を取ろう。
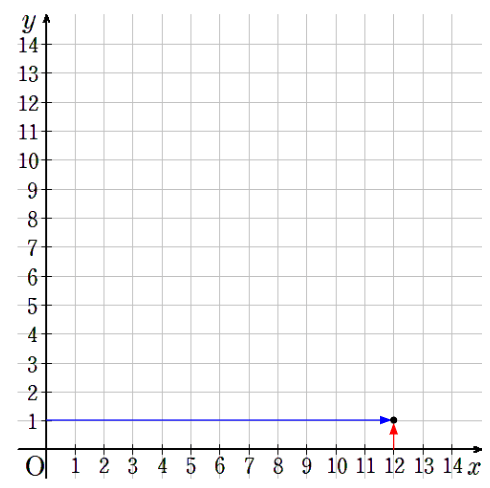
①~⑨までの点を1つのグラフに書くと次のようになるよ。
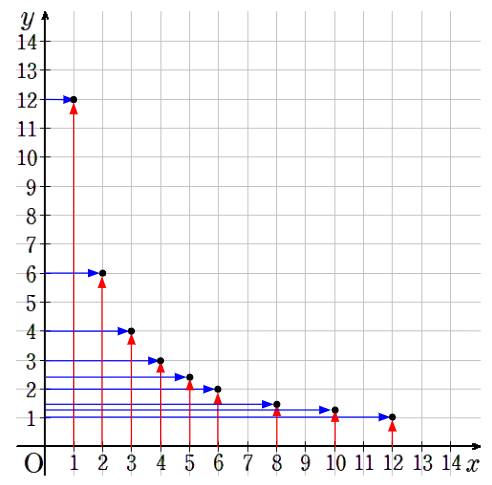
点だけに注目するよ。
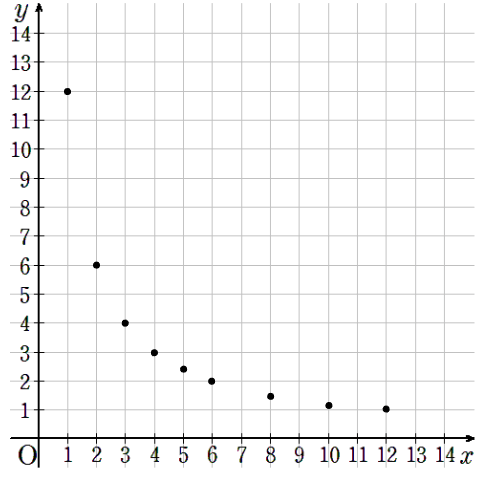
点を結んで曲線を引く
点を取ったら、点と点を順番に結んでいこう。
この時に注意する必要があるんだけれど、絶対に定規を使ってはダメだよ。
必ずフリーハンドで、なめらかに点を結んでいくようにしよう。

このように、反比例のグラフは今まで勉強してきた比例のグラフのように、直線のグラフにはならないんだ。
ちなみに1より小さいところと12より大きいところの点はとっていないけれど、曲線はグラフの端までのばしておこう。
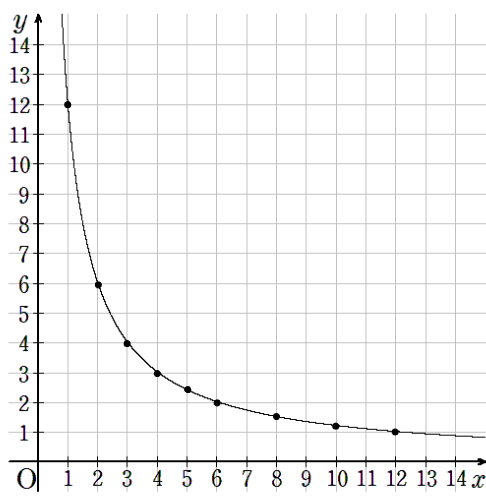
反比例の関係にある2つ以上の数量をグラフに表そう②
次の表は反比例の関係を表しています。
グラフに表しなさい。
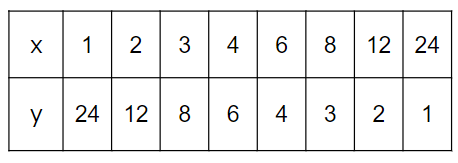
では、実際にグラフを書こう。
xとyの値の点をとる
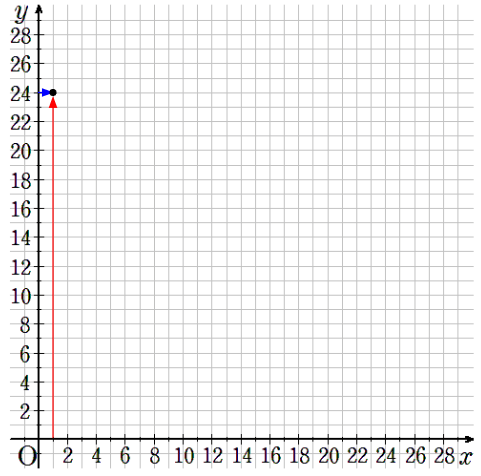
①x=1のとき、y=24
横軸が1で縦軸が24のところに点を取ろう。
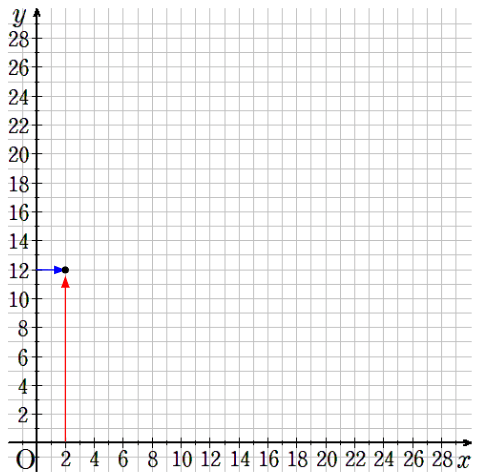
②x=2のとき、y=12
横軸が2で縦軸が12のところに点を取ろう。
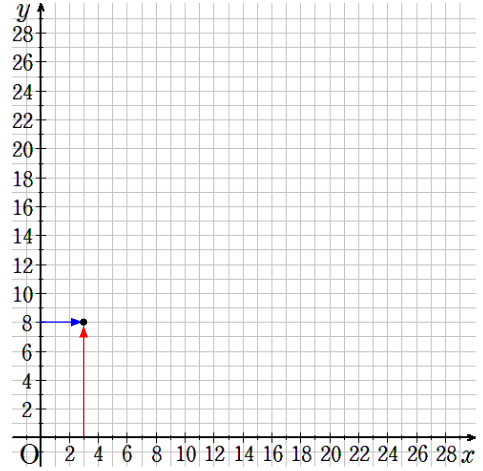
③x=3のとき、y=8
横軸が3で縦軸が8のところに点を取ろう。
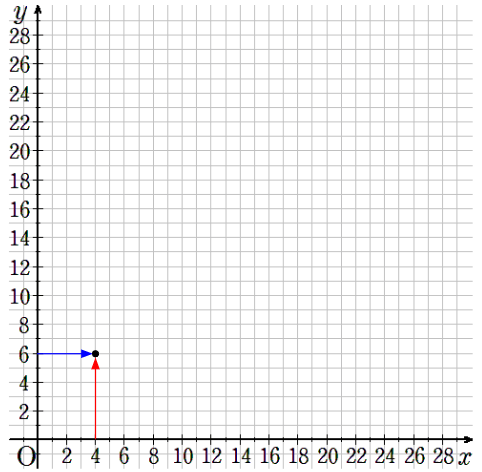
④x=4のとき、y=6
横軸が4で縦軸が6のところに点を取ろう。
⑤x=6のとき、y=4
横軸が6で縦軸が4のところに点を取ろう。
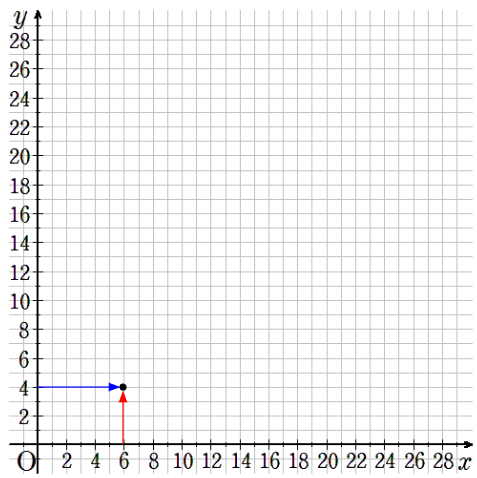
⑥x=8のとき、y=3
横軸が8で縦軸が3のところに点を取ろう。
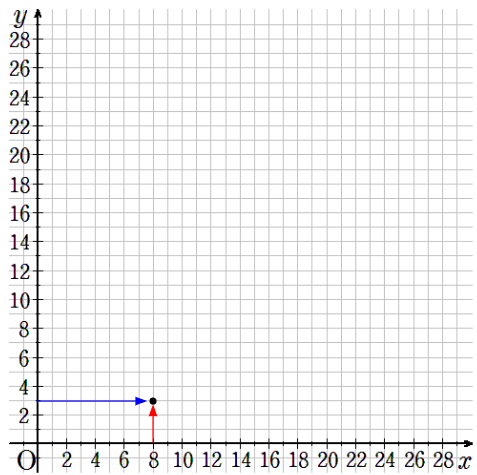
⑦x=12のとき、y=2
横軸が12で縦軸が2のところに点を取ろう。
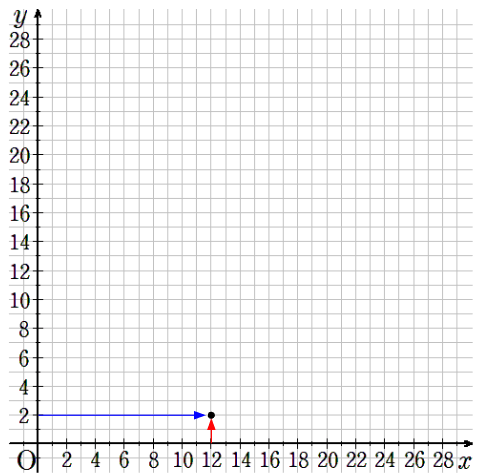
⑧x=24のとき、y=1
横軸が24で縦軸が1のところに点を取ろう。
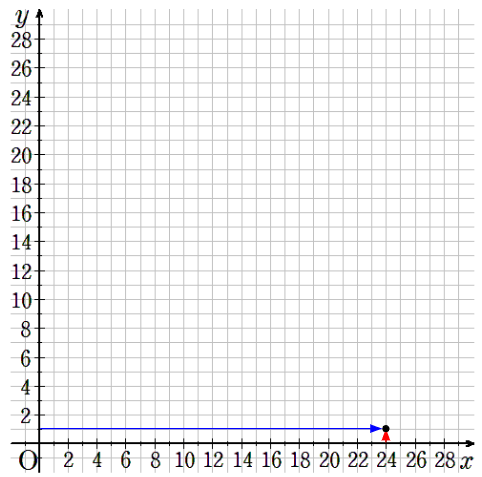
①~⑧までの点を1つのグラフに書くと次のようになるよ。
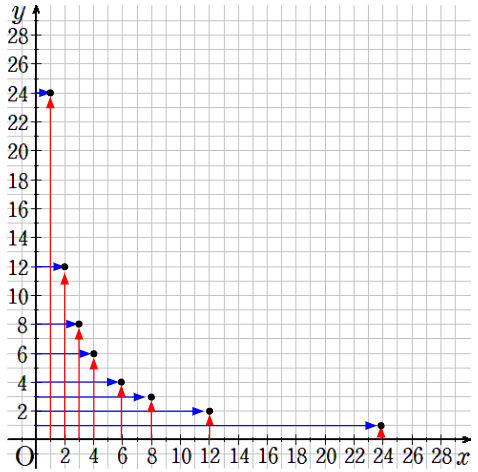
点だけに注目するよ。
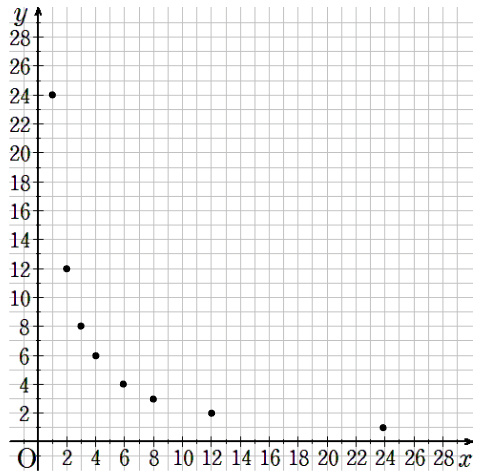
点を結んで曲線を引く
すべての点を通るように、定規は使わずになめらかな曲線を引こう。
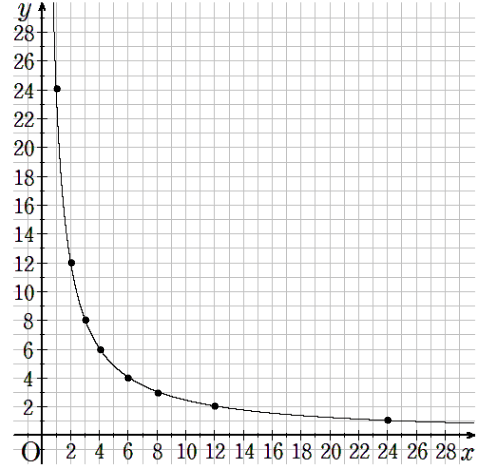
反比例のグラフの特徴
反比例のグラフにはどんな特徴があるのだろう?
2つの反比例のグラフを見てみよう。


結論からいうと、反比例のグラフの特徴は次の2つだよ。
反比例のグラフの特徴
- なめらかな曲線になること
- 0の点は通らないこと
曲線になることは、2つのグラフを書いてわかったよね。
では、なぜ反比例のグラフは0の点を通らないんだろう?
さっきの表を例に考えてみよう。

表を見ると、どこでもxとyをかけて24になっているよね。
この表にx=0を入れてみると次のようになるよ。
?はいくつになるかな?
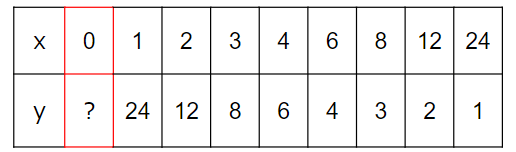
xとyをかけて24ということは
0と?をかけても24になるってことだね。
だけど、0にいくつをかけても24にはならないよね。
だから、x=0の点やy=0の点は存在しないんだ。
x=0の点やy=0の点が存在しないということは、「反比例のグラフは0の点は絶対に通らない」ということになるよ。
ちょっと難しかったかな?
中学1年生でも登場するから、今は「反比例のグラフは0の点は通らないんだ」と覚えておけばOKだよ。
反比例のグラフを書くときに気をつけること
反比例のグラフを書くときに気をつけなくてはいけないことがあるんだ。
それは「端まで意識すること」
反比例のグラフを書くときは、xとyの点をとって、なめらかな曲線で結ぶんだったよね。
ただ、グラフの端を書くときは次の2つの決まりを意識しなくちゃいけないんだ。
詳しくは中学1年生で勉強するから、今は「ふうん、そうなんだ」と思って覚えておこう。
反比例のグラフを書くときに気をつけること
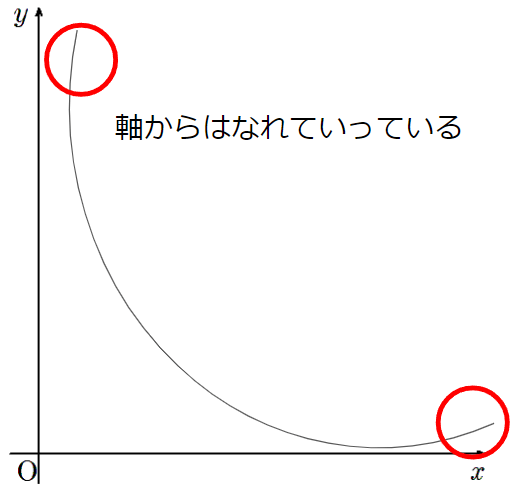
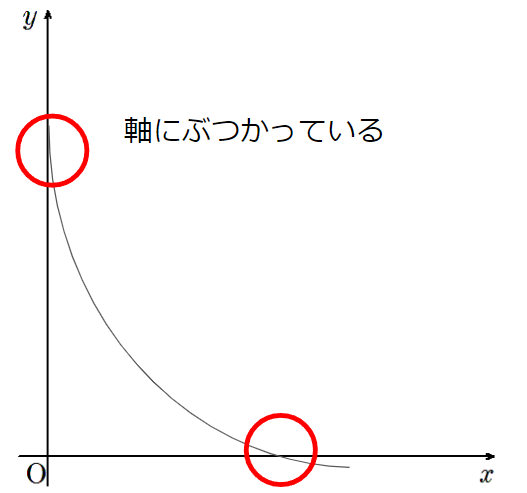
- 少しずつ、軸に近づいていくこと
- 軸にはぶつからないこと
例えばこんなグラフはダメだよ。
反比例と比例のグラフの違い
反比例のグラフと比例のグラフの違いをまとめてみたよ。
| 比例 | 反比例 |
| 直線になる | 曲線になる |
| 0の点を必ず通る | 0の点を絶対に通らない |

「反」がつくかつかないかで、グラフの形は全く違ってくるね。
「反比例のグラフ」まとめ
反比例のグラフの表し方
- 表を縦にみて、xとyの値をグラフに取る。
- すべての点を通るように、なめらかな曲線を書く。
※フリーハンドで書く
反比例のグラフの特徴
- なめらかな曲線になること
- 0の点は通らないこと
反比例のグラフを書くときに気をつけること
- 少しずつ、軸に近づいていくこと
- 軸にはぶつからないこと
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


