反比例とは？反比例する例と特徴をわかりやすく解説（練習問題）

小学校６年生の算数で学習する「反比例」について、反比例とはどういう意味か、反比例する例と反比例の特徴（反比例の性質）をわかりやすく解説するよ。

反比例の性質を使った問題の考え方も紹介するよ。

反比例とは？反比例する例と 特徴をわかりやすく解説（練習問題）のPDF（16枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 反比例する２つの数量の関係
• 反比例の性質
• 反比例の性質を使った問題
• 反比例の性質のまとめ

反比例する２つの数量の関係

これまで「比例」について勉強してきたね。
比例とは
ｘが2倍、3倍・・・になると、
ｙも2倍、3倍・・・になる関係のことだったよね。

では
今回の学習では比例に「反」がついた「反比例はんぴれい」について勉強していこう。

「反」というのは「反対」という意味。
比例とは反対の関係のことを反比例と呼ぶよ。
具体的に反比例の関係にある数量を見ていこう。

反比例の関係「速さ」と「時間」

「速さと時間と道のり」の関係のうち、「速さ」と「時間」は反比例の関係になっているんだ。
具体的な問題を見る前に、速さと時間と道のりの関係の復習をしよう。

速さと時間と道のりの関係

「速さと時間と道のりの関係」は、小学５年生のときに学習しているよ。
きっとみんな、次のような図を見たよね。

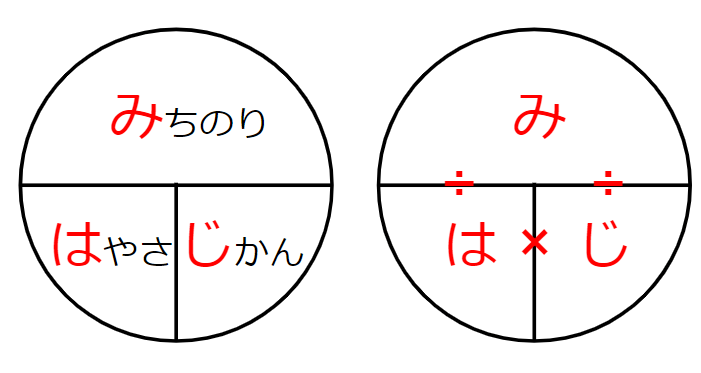
この図を覚えていたら、速さと時間と道のりの関係はばっちりだよ。

• 速さ＝道のり÷時間
• 時間＝道のり÷速さ　（今回の問題で使う式）
• 道のり＝速さ×時間

では実際に具体的な問題を考えてみよう。

家から駅までの道のりが６kmあるとするよ。

時速１kmで走った時にかかる時間は「道のり÷速さ」だから６÷１=６時間
時速２kmで走った時にかかる時間は６÷２=３時間
時速３kmで走った時にかかる時間は６÷３=２時間
時速４kmで走った時にかかる時間は６÷４=１.５時間
時速５kmで走った時にかかる時間は６÷５=１.２時間
時速６kmで走った時にかかる時間は６÷６=１時間

速さと時間の関係を表にすると次のようになるよ。

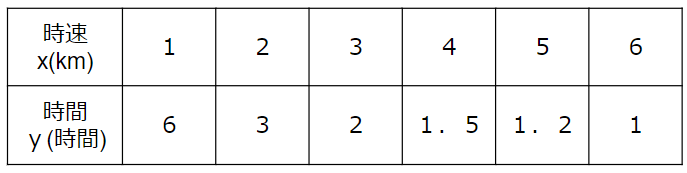
この表で表されているｘとｙの関係がまさに「反比例」なんだ。
比例のときのｘとｙの関係とは違うよね。
だって、比例のときだったら、ｘが２倍、３倍になるとｙも２倍、３倍になっていたからね。

それでは、この表をくわしく見ていこう。

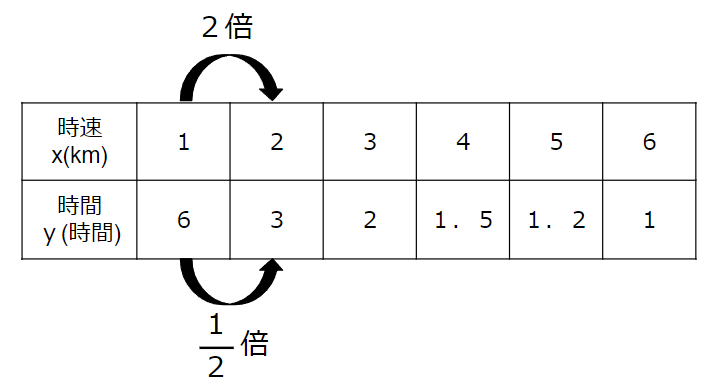
ｘが２倍になるとｙは\(\frac{1}{2}\)倍

ｘが２倍になると、ｙはどうなっているかな？
「何倍になっているか？」を求めるには、「比べる量÷もとにする量」を考えればよかったね。

ｙは６から３になっているのだから、
３÷６=\(\frac{1}{2}\)倍と求めることができるよ。

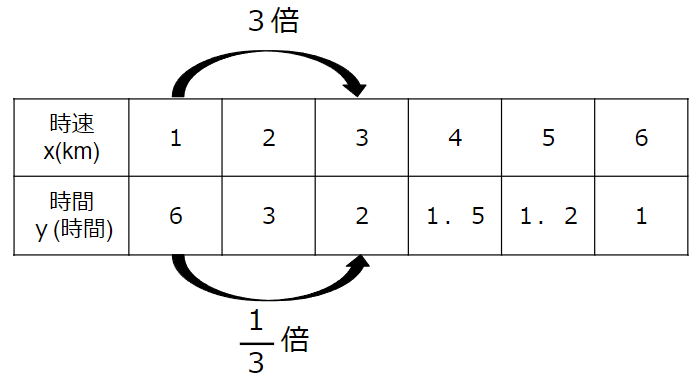
ｘが３倍になるとｙは\(\frac{1}{3}\)倍

ｘが３倍になると、ｙはどうなっているかな？
「何倍になっているか？」を求めるには、「比べる量÷もとにする量」を考えればよかったね。

ｙは６から２になっているのだから、
２÷６=\(\frac{1}{3}\)倍と求めることができるよ。

ｘが４倍になるとｙは\(\frac{1}{4}\)倍

ｘが４倍になると、ｙはどうなっているかな？
「何倍になっているか？」を求めるには、「比べる量÷もとにする量」を考えればよかったね。

ｙは６から１.５になっているのだから、
１.５÷６=\(\frac{1}{4}\)倍と求めることができるよ。

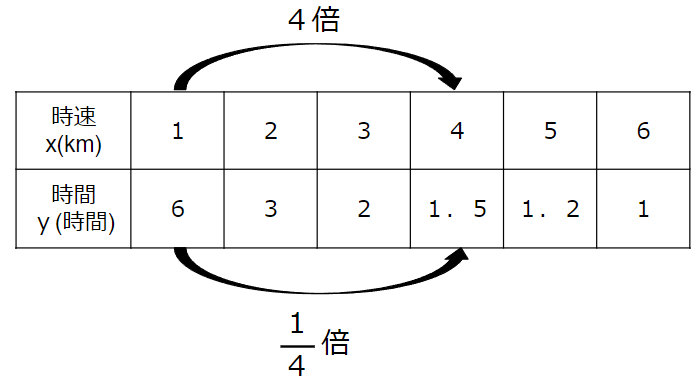
ｘが２倍、３倍、４倍になると、ｙは\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍、\(\frac{1}{4}\)倍

家から駅までの道のりが６kmで、
速さを時速ｘkm、時間をｙ時間とすると
次のような関係があることがわかったね。

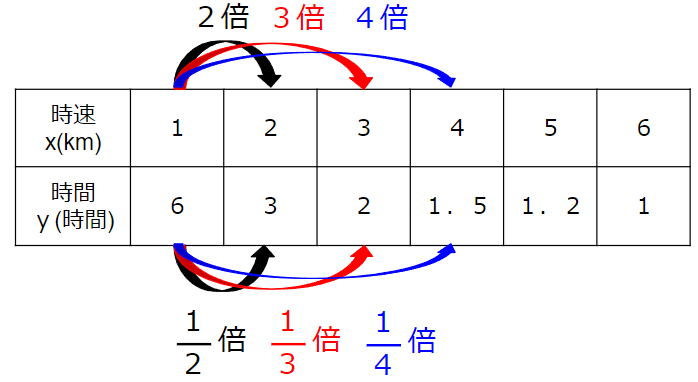
ｘが２倍、３倍、４倍になると、
ｙは\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍、\(\frac{1}{4}\)倍になっているね。

別の問題でも考えてみよう。

反比例の関係「平行四辺形の底辺と高さ」

「平行四辺形の底辺と高さ」は反比例の関係になっているんだ。
具体的な問題を見る前に、平行四辺形の面積の求め方の復習をしよう。

平行四辺形の面積の求め方

底辺×高さ

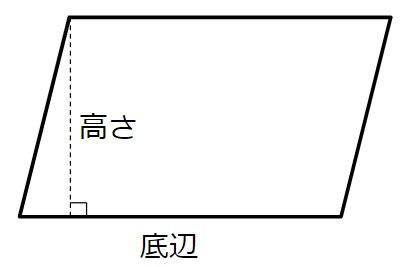
たとえば平行四辺形の面積が１２cm²のときを考えてみよう。

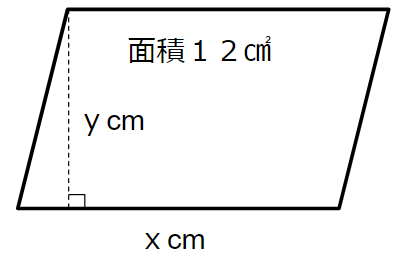
底辺ｘが３cmの場合

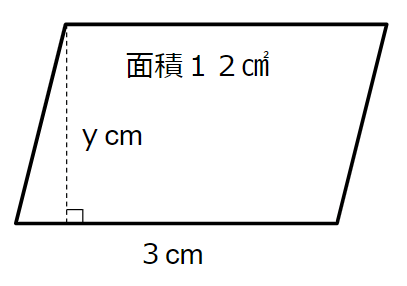
上の図を見て、高さｙは何cmになるかを考えよう。
底辺と高さをかけて１２cm²になるから
高さｙは４cmだとわかるね。

底辺ｘが６cmの場合

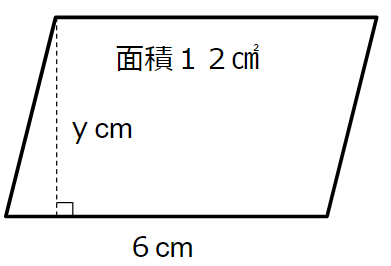
上の図を見て、高さｙは何cmになるかを考えよう。
底辺と高さをかけて１２cm²になるから
高さｙは２cmだとわかるね。

平行四辺形の底辺と高さの関係をまとめよう

底辺が１cmのときの高さは「面積÷底辺」になるから１２÷１=１２cm
底辺が２cmのときの高さは１２÷２=６cm
底辺が３cmのときの高さは１２÷３=４cm
底辺が４cmのときの高さは１２÷４=３cm
底辺が５cmのときの高さは１２÷５=２.４cm
底辺が６cmのときの高さは１２÷６=２cm
底辺が７cm以上は省略するね。

平行四辺形の底辺と高さの関係を表にしてみよう

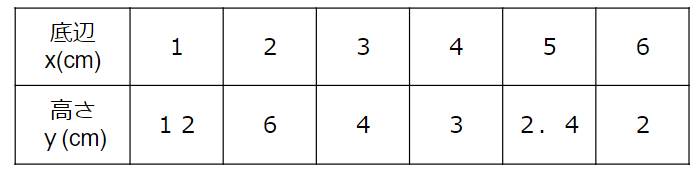
この表でｘとｙの関係を考えると次のようになるよ。

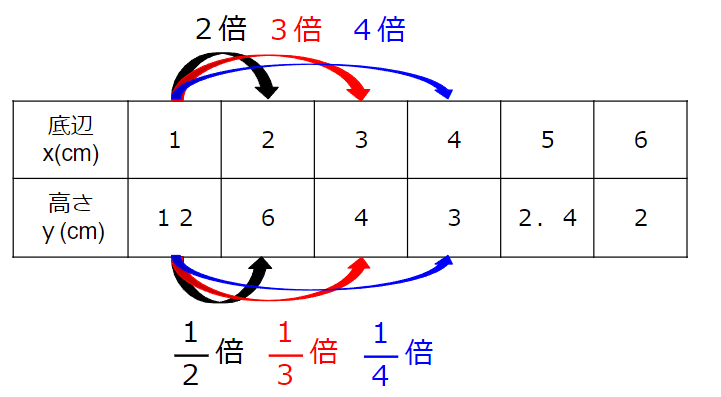
ｘが２倍、３倍、４倍になると、
ｙは\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍、\(\frac{1}{4}\)倍になっていることがわかるね。

反比例する２つの数量の特徴（反比例の性質）

「速さと時間の関係」、「平行四辺形の底辺と高さの関係」の２つの反比例の関係について考えたね。
まとめると次のような関係だったよ。

速さと時間の関係

平行四辺形の底辺と高さの関係

どちらも、
ｘが２倍、３倍、４倍になると、
ｙは\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍、\(\frac{1}{4}\)倍になっているね。

まさにこれが反比例の性質なんだ。

この性質はしっかり覚えておこう。

反比例の性質の発展

では、ちょっと発展的な質問をしてみるよ。
もし、ｘが\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍になったらｙはどうなるだろう？

さっきの「平行四辺形の底辺と高さの関係」の表をつかって、ｘが\(\frac{1}{2}\)倍になったときを確認してみよう。

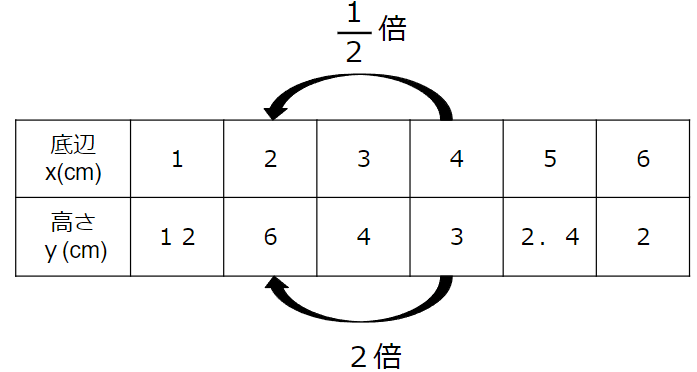
ｘが４から２に\(\frac{1}{2}\)倍になると
ｙは３から６になっていて、「２倍」になっているね。

ｘが６から２に\(\frac{1}{3}\)倍になると
ｙは２から６になっていて、「３倍」になっているね。

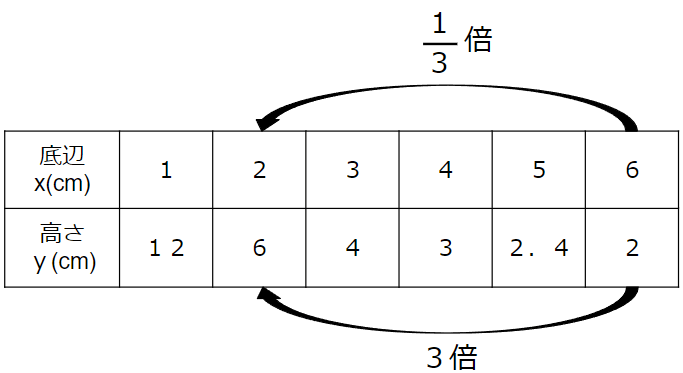
まとめると次のようになるよ。

「いやーなんか頭がこんらんしてきた」と思う人もいるよね。
比例よりややこしいことは間違いないね。

そんな人にとっておきの考え方があるよ。

反比例っていうのは、
ｘが〇倍になったら、ｙは\(\frac{１}{〇}\)倍
ｘが\(\frac{１}{〇}\)倍になったら、ｙは〇倍
になるんだ。

つまりｘとｙは逆数の関係にあることを覚えておこう。

反比例の性質を使った問題

「反比例になるか」「反比例にならないか」を考える問題

下の表は、まわりの長さが１０cmの長方形の縦の長さと横の長さを表したものです。
縦の長さｘと横の長さｙは反比例の関係ですか。

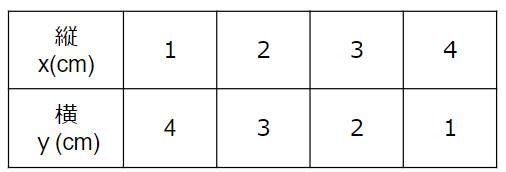
反比例の性質を思い出してみよう。

ｘが２倍になるとき、ｙが\(\frac{1}{2}\)倍になっているか表で見てみよう。

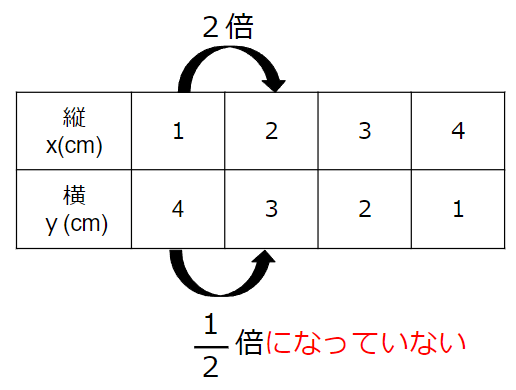
ｘが３倍になるとき、ｙが\(\frac{1}{3}\)倍になっているか表で見てみよう。

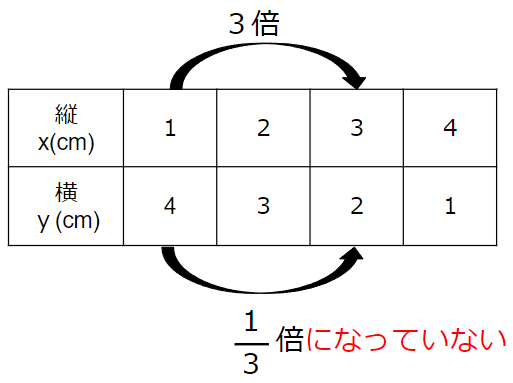
ｘが４倍になるとき、ｙが\(\frac{1}{4}\)倍になっているか表で見てみよう。

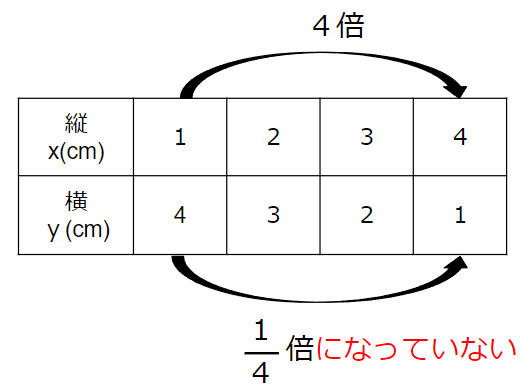
ｘの値が２倍、３倍、４倍・・・になっても
ｙの値は\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍、\(\frac{1}{4}\)倍になっていない
から
反比例とはいえないよ。

反比例の性質を使って表の空らんをうめる問題

次の表のｘとｙは反比例の関係にあります。
表の空らんに当てはまる数字を答えなさい。

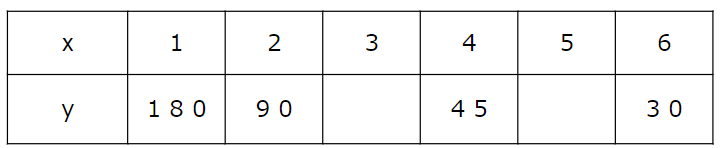
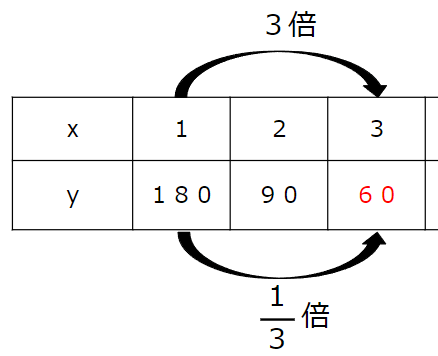
ｘが「３」のときのｙの値を求めよう

ｘの「１」と「３」に注目するよ。
ｘが１から３で３倍になっているから、
ｙは\(\frac{1}{3}\)倍になるはずだね。

180×\(\frac{1}{3}\)=60

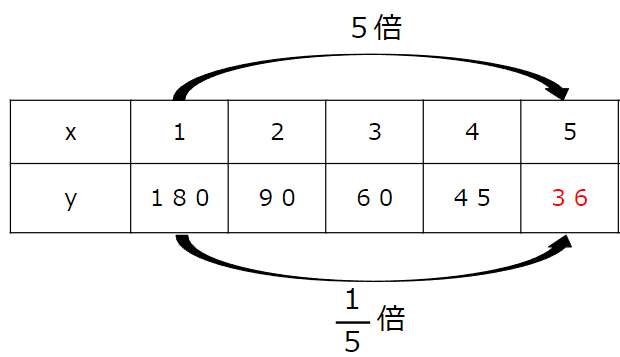
ｘが「５」のときのｙの値を求めよう

ｘが１から５で５倍になっているから、
ｙは\(\frac{1}{5}\)倍になるはずだね。

180×\(\frac{1}{5}\)=36

反比例の性質のまとめ

反比例の性質を比例と比べてみよう。
比例と反比例は２つセットで覚えるといいよ。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

1. 匿名 より:

   2024年1月16日 5:26 PM

   わかりやすかった。

   返信