「分数の掛け算」分数のかけ算のやり方をくわしく解説(練習問題)
小学校6年生の算数で学習する「分数の掛け算」について、分数のかけ算のやり方をわかりやすく解説するよ。
とちゅうで約分する場合など、大切なポイントを紹介。練習問題にもチャレンジして、分数の掛け算をマスターしよう!
分数のかけ算を考えよう
小学校の算数では、これまで「分数のたし算」や「分数のひき算」を学習してきたよね。
6年生の算数では、「分数のかけ算」をやっていくよ。
ちなみにこのあとには「分数のわり算」もでてくるよ。
かけ算ができたら、わり算も楽勝だから、しっかり分数のかけ算をマスターしようね。
まずは、次のような分数×整数のかけ算に挑戦してみよう。
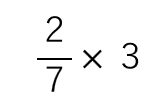
考え方を2つ紹介するね。
分数×整数のかけ算の考え方①
図を使って考えてみよう。
下のような1L(リットル)の水が入るタンクがあったとしよう。
\(\frac{2}{7}\)というのは、タンクに入る水の量を、7個に分けたうちの2個分に水が入っているということになるよね。
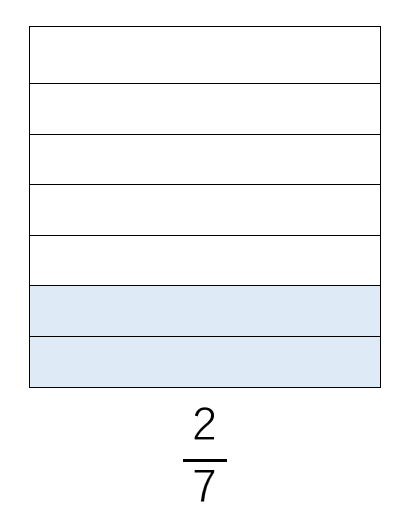
ということは、\(\frac{2}{7}\)×3というのは、下のように\(\frac{2}{7}\)の水が入ったタンクが3つあるイメージになるよ。

この3つのタンクに入っている水を、1つのタンクにまとめると
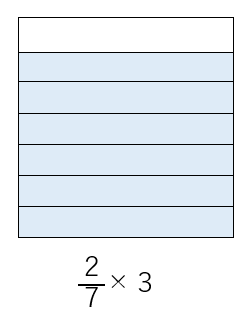
こうなるよね。
上の水の量は、
「\(\frac{2}{7}\)×3」とも表せるけど、
「\(\frac{6}{7}\)」でもいいよね。
だって、7個に分けた6個分に水が入っているんだもん。
だから、
\(\frac{2}{7}\)×3=\(\frac{6}{7}\)になるんだよ。
分数×整数のかけ算の考え方②
今度は図ではなく、式で考えてみよう。
\(\frac{2}{7}\)というのは、\(\frac{1}{7}\)が2個分のことだよね。
\(\frac{2}{7}\)×3というのは、
(\(\frac{1}{7}\)の2個分)のセットが3個ある感じだよね。
だから
\(\frac{1}{7}\)が(2×3)個あるということだよ。
これは、次のような式で計算できるよ。
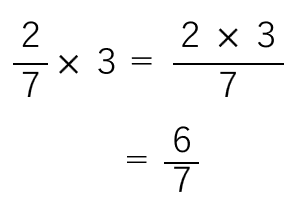
だから、
\(\frac{2}{7}\)×3=\(\frac{6}{7}\)。
図を使った考え方と答えが同じになっているね。
分数×整数のかけ算のポイント
\(\frac{2}{7}\)×3=\(\frac{6}{7}\)になることを、2つの考え方を使って説明してきたね。
分数×整数のかけ算のポイントは、整数の数字が分子(上)に来るということ。
さっきの問題だったら、整数3が分子(上)に来たよね。
分数×整数のかけ算のポイント
- 整数の数字が分子(上)に来る
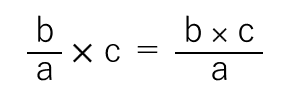
計算のとちゅうで約分できる場合の分数のかけ算
分数のかけ算の中には、とちゅうで「約分」ができる場合があるよ。
次の分数のかけ算をやってみよう。
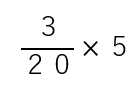
さっきのポイントを使ってやると、
整数は分子(上)に来るから次のような式になるよね。
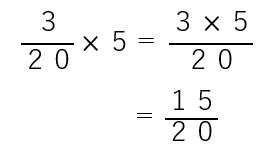
ただ、分母の20も分子の15も5で割れるから、約分できるね。
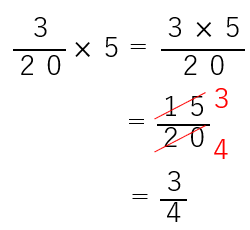
もっと簡単にやる方法があるから説明していくね。
計算のとちゅうで約分
簡単に計算する方法が「途中で約分」だよ。
さっきの問題の場合だったら、
下の場所で、分母の20と分子の5を約分することができるよ。
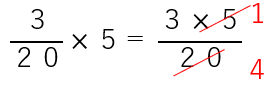
そのあとは今まで同じように計算すると
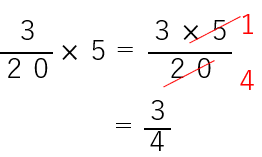
答えは同じになっているね。
でも、とちゅうで約分をしてしまうほうが、最後に約分をする方法よりも計算が小さい数になっているので楽に求めることができるよ。
よけいな計算ミスをふせぐこともできるので、とちゅうで約分ができないか?を考えながら解くのがおすすめだよ。
分数のかけ算の問題
それでは、実際に分数のかけ算の問題に挑戦してみよう。
\(\frac{4}{9}\)×2を計算しなさい。
整数の数字は分子(上)に来るから、この問題では2が分子(上)に来るよ。
だから次のように計算できるね。
\(\frac{4}{9}\)×2
=\(\frac{4×2}{9}\)
=\(\frac{8}{9}\)
\(\frac{3}{16}\)×5を計算しなさい。
整数の数字は分子(上)に来るから、この問題では5が分子(上)に来るよ。
だから次のように計算できるね。
\(\frac{3}{16}\)×5
=\(\frac{3×5}{16}\)
=\(\frac{15}{16}\)
\(\frac{3}{16}\)×4を計算しなさい。
整数の数字は分子(上)に来るから、この問題では4が分子(上)に来るよ。
だから次のように計算できるね。
\(\frac{3}{16}\)×4
=\(\frac{3×4}{16}\)
=\(\frac{12}{16}\)
ここで終わったらだめだよ。だって約分できるからね。
\(\frac{12}{16}\)
=\(\frac{3}{4}\)
ただ、次のような感じで、
計算のとちゅうで約分すれば、もっと速く計算できたね。
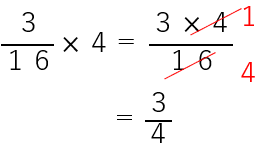
\(\frac{4}{25}\)×100を計算しなさい。
急に数が大きくなったね。数が大きい場合は、なんとなく、「計算のとちゅうで約分するのかな?」と思っておこう。
整数の数字は分子(上)に来るから、この問題では100が分子(上)に来るよ。
だから次のように計算できるね。
\(\frac{4}{25}\)×100
=\(\frac{4×100}{25}\)
ここでストップ。
4×100=400としてもいいけど、約分がめんどうくさいよね。
だから、先に約分をしてしまおう。
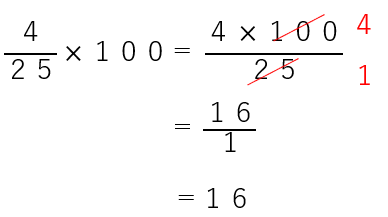
計算のとちゅうで約分した方が速く計算ができるよ。
「分数の掛け算」まとめ
分数×整数のかけ算のポイント
- 整数の数字は分子(上)に来る
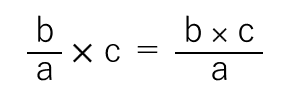
- b×cの計算をする前に、aとcで約分できるならしておく。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。

-
私は、算数が苦手なんですけど、こういうふうにやり方をみてやり方を覚えていくと算数の成績もよくなりました。
ありがとうございます!
これからも、算数のいろいろなやり方を覚えてもっとよくなりたいです。!


私は、算数が苦手なんですけど、こういうふうにやり方をみてやり方を覚えていくと算数の成績もよくなりました。
ありがとうございます!