「分数の割り算」やり方・なぜひっくり返すのかを説明（練習問題）

小学校６年生の算数で学習する「分数の割り算（わり算）」について、分数÷整数の計算の仕方・やり方を簡単に説明しているよ。

分数の割り算では、なぜひっくり返すのかをくわしく解説。
問題にもチャレンジして分数の割り算をマスターしよう。

「分数の割り算」やり方なぜひっくり返すのかを説明（練習問題）のPDF（11枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

分数の割り算を考えよう

「分数の掛け算」の解説ページでは、分数×整数の掛け算のやり方を学習したね。
では、今度は分数÷整数の割り算に挑戦してみよう。

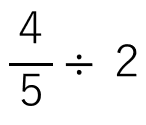
考え方を２つ紹介するね。

分数÷整数の割り算の考え方①

図を使って考えてみよう。

下のような、１Lの水が入るタンクがあったとしよう。
\(\frac{４}{５}\)っていうのは、５個に分けたうちの４個分に水が入っているということになるよね。

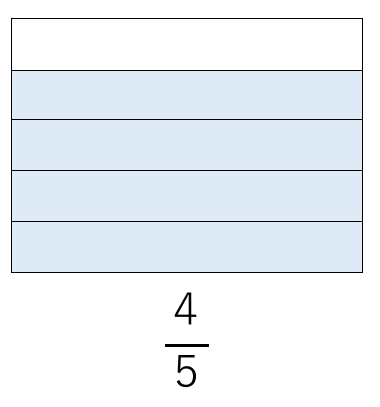
この後がポイントなんだけど、
\(\frac{４}{５}\)の水って次のようにも考えられるよね。
（１段を２つの部屋に分けたよ）

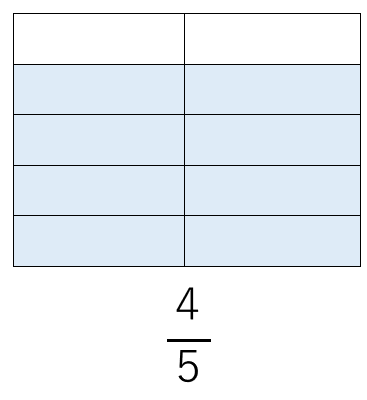
ということは
\(\frac{４}{５}\)÷２っていうのは、
\(\frac{４}{５}\)の半分のイメージだね。

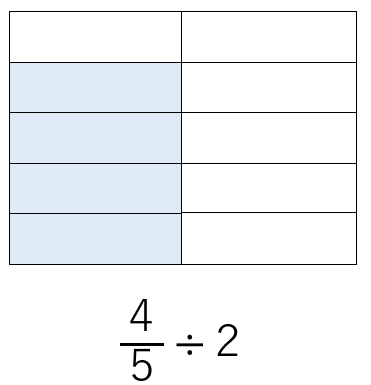
上の図の量は、１０個に分けたうちの４個分に水が入っているから、
\(\frac{４}{１０}\)
約分して
\(\frac{２}{５}\)
と表すことができるね。

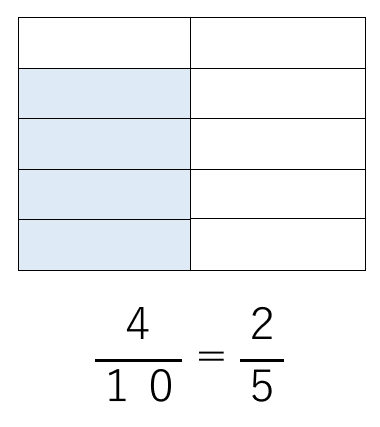
だから、
\(\frac{４}{５}\)÷２＝\(\frac{２}{５}\)
と計算することができるよ。

分数÷整数の割り算の考え方②

今度は図ではなく、式で考えてみよう。

\(\frac{４}{５}\)は、\(\frac{１}{５}\)が４個分だよね。

\(\frac{４}{５}\)÷２っていうのは
\(\frac{１}{５}\)の４個分が半分になるイメージだね。

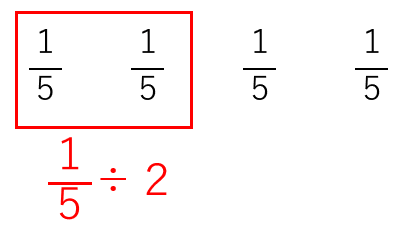
だから
\(\frac{１}{５}\)が（４÷２）個あるってことになるね。

次のような式で計算できるよ。

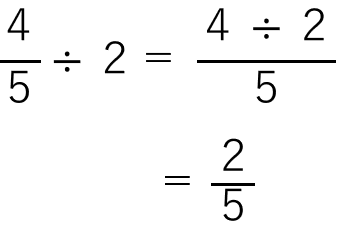
図を使った考え方と答えが同じになっているね。

\(\frac{４}{５}\)÷２＝\(\frac{２}{５}\)になることを
２つの考え方を使って説明してきたね。

分数÷整数の割り算のポイントは、
整数の数字が分子（上）に来るということだよ。
かけ算の時と同じだね。

さっきの問題だったら、整数２が分子（上）に来たよね。

分数÷整数の割り算のポイント

整数の数字を分子（上）に移動させて割り算をする

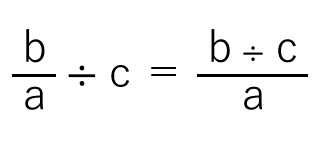
分数が割り切れないときの割り算の考え方③

それでは、たとえば次の計算をしてみよう。

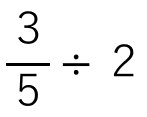
「÷２」を分子（上）にもっていったらいいから次のようになるよね。

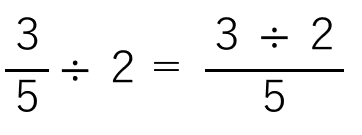
でも、「３÷２」ってどうかな？
割り切れないから、こまってしまったね。

\(\frac{３}{５}\)÷２の計算のように、
分子が割り切れないときは　さっきの「割り算のポイント」とは計算の仕方を変えなくてはいけないんだ。

「÷２」ができるようにするために、
\(\frac{３}{５}\)を少しいじろう！

\(\frac{３}{５}\)の分母と分子を「×２」しよう。

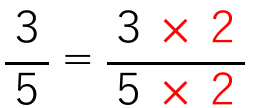
こうすると、さっきの式は次のようになるよ。

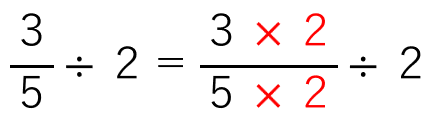
「÷２」を分子にもっていったら次のようになるよね。

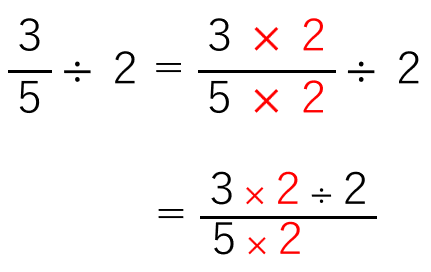
分子は「２÷２＝１」だから

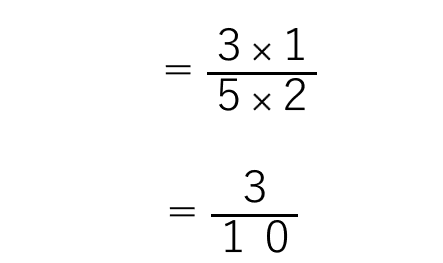
と求めることができるね。
この問題の大事なポイントは「÷２」するために
分母と分子に２をかけることだよ。

\(\frac{３}{５}\)÷２の計算のように、分子がわり切れないときは、
分母と分子に「÷〇」の〇の数をかければよいということだね。

分母と分子に同じ数をかけてもいい理由

さっき\(\frac{３}{５}\)の分母と分子を「×２」したよね。
「そんな勝手なことをしてもいいの？」と不安に思ってしまう人もいるかもしれないね。

分数の特徴なんだけれど、
分母と分子に同じ数をかけても、分数の大きさは変わらないよ。

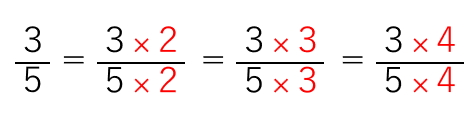
分数を約分するときだって、分子と分母を同じ数で割っているよね。
約分しても、その分数があらわす大きさ自体は変わらないよね。
それと同じ考え方だね。

分数の割り算のポイント（割る数をひっくり返して掛け算にする）

ここであることに気付いてほしいんだ。
さっきの計算を振り返ろう。

四角で囲った、赤字のところを見てみよう。

割られる分数にの分母と分子に、割る数である整数と同じ数をかけたことで、
結果的には\(\frac{３}{５}\)÷２の「２」がひっくり返って分母に来て、かけ算をすることになっているよね。

ここが分数の割り算の重要ポイントなんだけれど、
「÷〇」の数はひっくり返って分母に来て、かけ算になるんだよ。

文字で表すと次のようなイメージ

分数÷整数の割り算のポイント（超重要）

整数の数字を分母（下）に移動させて（ひっくり返して）かけ算する

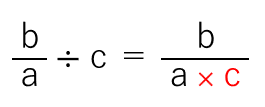
さっきもポイントがあって「どういうこと？」ってなる人もいるよね。

さっきのポイントは、
分子の数が割り切れる場合にしか使えないよ。

だから上のポイントを覚えておけばどんな問題にも使えるからね。

分数÷整数の割り算のポイント（分子が割り切れる場合しか使えない）

整数の数字を分子（上）に移動させて割り算する

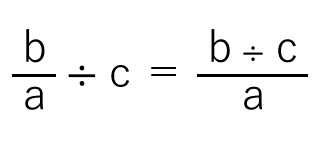
分数÷整数の割り算のポイント（分子が割り切れない場合でも使える）

整数の数字を分母（下）に移動させて（ひっくり返して）かけ算する

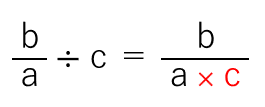
分数の割り算の問題

それでは、分数の割り算の問題にチャレンジしてみよう。

\(\frac{４}{９}\)÷２を計算しなさい。

整数の数字２を分母（下）に移動させてかけ算すればいいから
\(\frac{４}{９}\)÷２
＝\(\frac{４}{９×２}\)
＝\(\frac{４}{１８}\)　　←約分しよう
＝\(\frac{２}{９}\)

この問題だったら、分子の「４÷２」がわり切れるから
次のようなやり方でやってもいいよね。
\(\frac{４}{９}\)÷２
＝\(\frac{４÷２}{９}\)
\(\frac{２}{９}\)

\(\frac{７}{９}\)÷３を計算しなさい。

整数の数字３を分母（下）に移動させてかけ算すればいいから
\(\frac{７}{９}\)÷３
＝\(\frac{７}{９×３}\)
＝\(\frac{７}{２７}\)

\(\frac{２４}{３６}\)÷１２を計算しなさい。

整数の数字１２を分母（下）に移動させてかけ算すればいいから
\(\frac{２４}{３６}\)÷１２
＝\(\frac{２４}{３６×１２}\)

ここで、まさか３６×１２を計算したりしないよね。
分母の１２と、分子の２４で約分してから計算しよう。
＝\(\frac{２}{３６×１}\)
＝\(\frac{２}{３６}\)
＝\(\frac{１}{１８}\)

この問題だったら、分子の「２４÷１２」がわり切れるから
次のようなやり方でやってもいいよね。
\(\frac{２４}{３６}\)÷１２
＝\(\frac{２４÷１２}{３６}\)
＝\(\frac{２}{３６}\)
\(\frac{１}{１８}\)

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。