「拡大図と縮図」とは?拡大図と縮図の特徴と条件(練習問題)
小学校6年生の算数で学習する「拡大図」と「縮図」について、拡大図とはなにか、縮図とはなにか、それぞれ拡大図・縮図であるかどうかの条件となる特徴をわかりやすく解説するよ。
拡大図と縮図についての問題もあるので、ぜひチャレンジしてみよう!
拡大図とは
普段生活しているときに「拡大」という言葉を聞いたことはあるかな?
何かをコピーするときに「見えにくいから少し拡大しよう」とか、
地図が見えにくいときに「この部分だけ拡大してみよう」とかいうように使われたりするよね。
あと、車のカーナビやグーグルマップなどで「拡大ボタン」とかあるよね。
「拡大」とは、「ひろげて大きくする」ことだよ。
下のような感じのイメージだね。
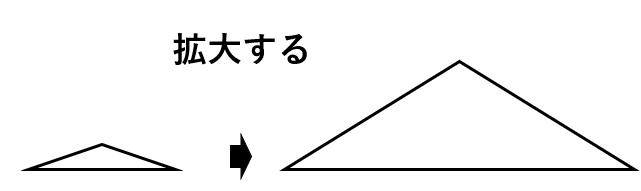
拡大した図のことを「拡大図」というよ。
「なんだ!簡単じゃん」と思うかもしれないけれど、ここからが重要。
中学3年生でも出てくる内容だからしっかり理解しておこうね。
拡大図とは「形を変えないで大きくした図」
「拡大図」とは、かんたんに言うと「拡大した図のこと」なんだけれど、
教科書ではもっとこまかく「形を変えないで大きくした図」と書いてあるよ。
つまり、拡大図は形が変わってしまってはいけないんだね。
たとえば、下の図は、大きくなっていはいるけれど、もとの図とは形が変わってしまっているから拡大図とは言えないということだよ。
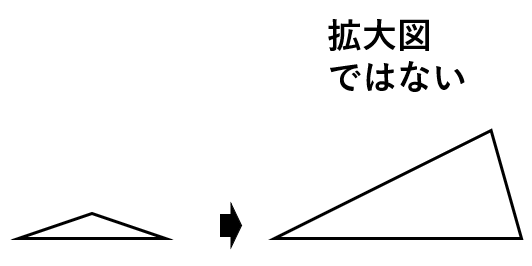
拡大図とは
形を変えないで大きくした図
→大きくなっていても、形が変わってしまっては「拡大図」ではない。
拡大図の特徴
拡大図は「形を変えないで大きくした図」ということだけれど、「形を変えない」ってどういうことだろう?
拡大図の特徴について学習すると、「形を変えない」とはどういうことかがわかるよ。
たとえば次のような2つの図形を考えてみよう。
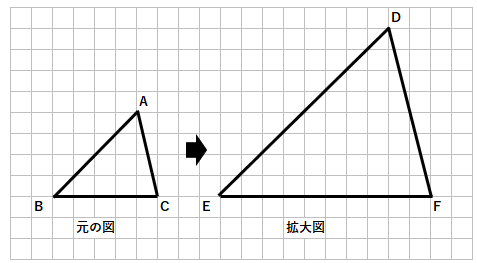
結論からいうと、この2つの図形は形が同じで、△DEFは、△ABCの拡大図といえるよ。
なぜこの2つの三角形は「形が変わらない」といえるのか、この△DEFと△ABCをくらべて、拡大図にはどんな特徴があるか考えてみよう。
ポイントは、対応する角の大きさと辺の長さだよ。
拡大図の特徴
- 対応する角の大きさが等しい
(拡大したら重なる角の大きさが等しい)
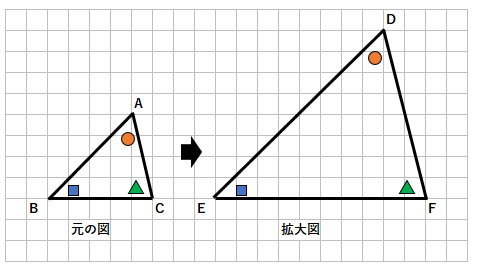
- 対応する辺の長さの比はすべて等しい
(拡大したら重なる辺の長さの比が等しい)
AB:DE=1:2
BC:EF=1:2
AC:DF=1:2
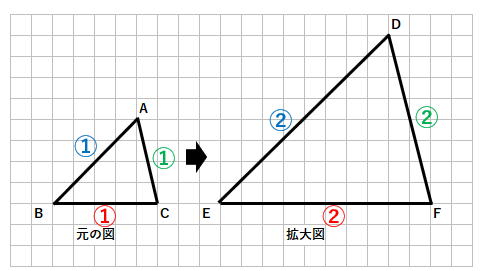
→すべての辺の長さが2倍になっているよね。
拡大図の特徴はわかったかな?
拡大図には、
- 対応する角の大きさが等しい
- 対応する辺の長さの比がすべて等しい
という特徴があるんだね。
つまり、この2つの特徴が当てはまることが「形が変わらない」ということ。この2つの特徴が当てはまれば「拡大図」と呼べるんだね。
拡大図の問題
それでは拡大図の特徴に注目して、問題をといてみよう。
次の中でアの拡大図はどれか?
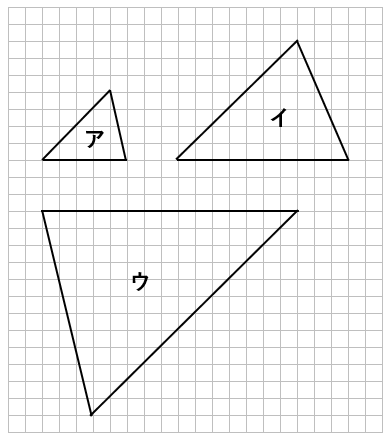
拡大図は「形を変えないで大きくした図」だけれど、イもウも、ぱっと見ではアと同じ形のように見えるね。
そういうときは、拡大図の特徴を思い出してみよう。
イとウがそれぞれ、拡大図の特徴に当てはまるかを確認するよ。
- 対応する角の大きさが等しいかどうか
角度を確認した結果、アとウはすべての対応する角の大きさが等しいけど、
イは1つしか等しくないことがわかるよ
→なので、イは拡大図ではないね。
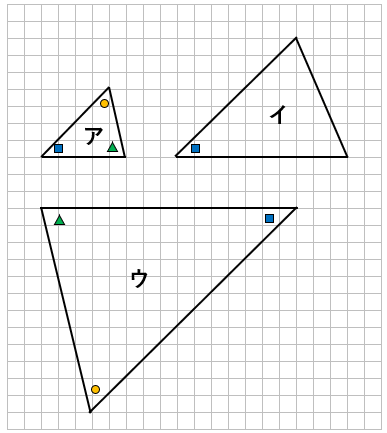
- 対応する辺の長さの比はすべて等しいかどうか
アとウの対応する辺を比べると、すべての辺の長さの比が1:3になっているよ。
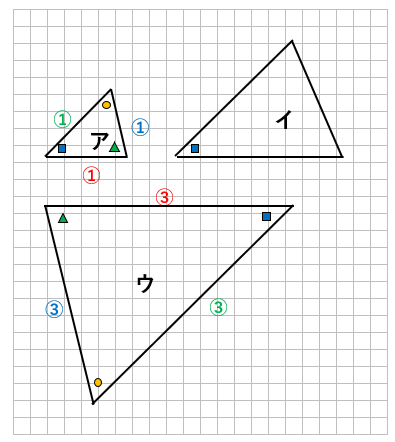
対応する全ての角の大きさが等しくて、対応する全ての辺の比がひとしいので、アの拡大図はウだということがわかったね。
縮図とは
拡大図とは、形を変えずに大きくした図のことだったね。
拡大図とは逆に、「形を変えずに小さくした図」のことを「縮図」というよ。
縮図のイメージは次の通り
「拡大図」とちがって、「縮小図」とは言わないので注意しよう。
縮図とは
形を変えずに小さくした図のこと
※「縮小図」と言わないように注意しよう!
縮図の特徴
縮図も、「形を変えないで」という条件があったよね。
なので、縮図の特徴はも拡大図と同じで次の通りだよ。
縮図の特徴
- 対応する角の大きさが等しい
(縮小したら重なる角の大きさが等しい)
- 対応する辺の長さの比はすべて等しい
(縮小したら重なる辺の長さの比が等しい)
縮図の問題
それでは縮図の問題にも挑戦してみよう。
右の長方形は、左の長方形の縮図といえるだろうか?
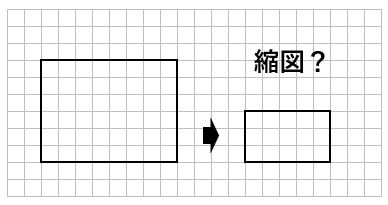
答えは、「縮図とは言えない」よ。
縮図の特徴を思い出してみよう。
- 対応する角の大きさが等しいかどうか
→長方形は4つの角度が90度だから、角の大きさは等しいよね。
ひとつ目の特徴はクリアしたね。
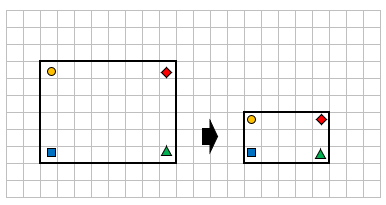
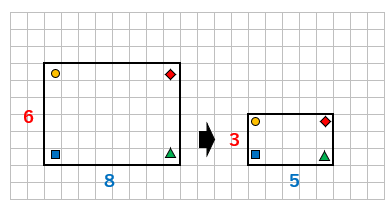
- 対応する辺の長さの比はすべて等しいかどうか
縦の長さだけみると、6と3で2:1になっているんだけれど
横の長さが8と5だから、2:1になっていないね。
だから、縮図とはいえないよ。
拡大図も、縮図も、2つの特徴両方をクリアしないといけないことに注意しようね。
拡大図と縮図の練習問題
下の四角形EFGHは、四角形ABCDの2倍の拡大図です。
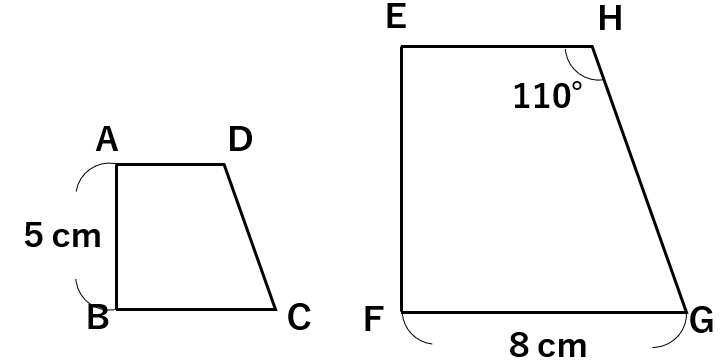
(1)辺EFの長さを求めなさい。
(2)辺BCの長さを求めなさい。
(3)角Dの大きさを求めなさい。
(1)10cm
2倍の拡大図ということは、すべての辺の比が1:2になるということ
だから、辺ABの長さを2倍したら、辺EFになるよ。
5×2=10
(2)4cm
2倍の拡大図ということは、すべての辺の比が1:2になるということ
だから、辺FGの長さを2で割ったら、辺BCになるよ。
8÷2=4
(3)110°
拡大図は対応する角の大きさは等しくなるよね。
角Dと対応するのは角Hだから110°だということがわかるよ。
拡大図と縮図のまとめ
拡大図と縮図は、
元の図形の形を変えずに、大きくしたり小さくした図形のこと。
縮小図とは言わないようにしよう。
拡大図や縮図は
中学3年生の「相似」という単元で再び登場するから
今のうちにマスターしておこう。
拡大図と縮図の特徴は次の通りだよ。
拡大図と縮図の特徴
- 対応する角の大きさが等しい
- 対応する辺の長さの比はすべて等しい
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



hello