「組み合わせが何通りあるのか」の求め方を解説（表と図で表そう）

小学校６年生の算数で学習する「組み合わせ」について、落ちや重なりがないように組み合わせが何通りあるかを調べる方法をわかりやすく解説するよ。

表を使って組み合わせが何通りあるか求める方法、図を使って組み合わせが何通りあるか求める方法、それぞれをくわしく紹介。

「組み合わせが何通りあるのか」の求め方を 解説（表と図で表そう）のPDF（10枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 組み合わせを表で表して調べてみよう
• 組み合わせを図で表して調べてみよう
• 組み合わせの練習問題
• 「組み合わせ」まとめ

組み合わせを表で表して調べてみよう

「並び方が何通りあるか」の学習では、４つの数字を並べたときに何通りの並べ方があるかなどを表や図であらわして調べたね。

こんどは、数字などを選ぶときに、「組み合わせは何通りあるか」を表や図をつかってあらわす方法を考えていくよ。

たとえば、次のような「組み合わせが何通りあるか」を考えてみよう。

４チームから２チームを選んで、組み合わせる問題だよ。
「組み合わせの問題」はよくテストでも出てくるし、中学生になっても勉強する内容なので、しっかりできるようにしておこう。

A、B、C、Dの４チームの中から２チームを選ぶくらいなら、頭だけで考えて、「AとB」「BとC」「CとD」「AとC」「AとD」「BとD」の６通りかな？
と求めることができるかもしれないね。

でも、もし４チームじゃなくて１６チームだったらどうだろう。
数え忘れが起きてしまいそうじゃないかな？
「あれ、さっきと同じ組み合わせを書いちゃった」
「しまった、この組み合わせ書き忘れていたよ」
「この組み合わせ、さっき書いたっけ？」となりそうだね。

組み合わせの問題を解くポイントは「数え忘れがないようにする」ことなんだ。
なので、きちんと「表」であらわして考えてみよう。

組み合わせを「規則ただしく」表で書く方法

今回のように、「チームの対戦の組み合わせ」を考える場合は、下のような「対戦表」を描いて考えるとわかりやすいよ。

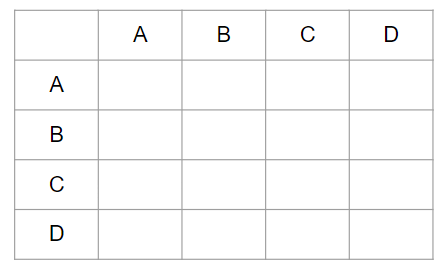
対戦表の見方を紹介するね。

対戦表の見方

①下のオレンジの場所は、「AとBが交わる」から、「AとBが対戦する」という意味になるんだ。

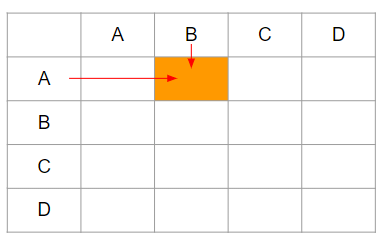
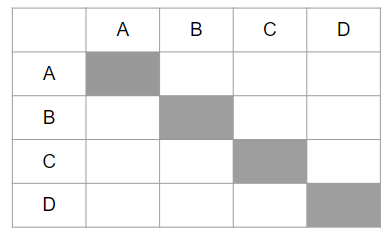
②下の灰色の場所は、それぞれ「AとA」、「BとB」、「CとC」、「DとD」が交わっているけれど、「自分自身と対戦」することはできないよね。だから、この部分は組み合わせにはいれないよ。

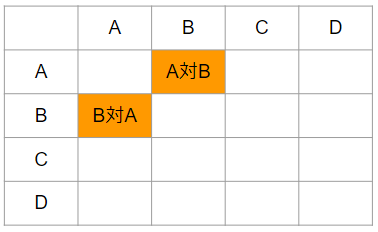
③下のオレンジの場所は、「A対B」と「B対A」を表しているよ。
ただ、これって両方とも「AとBが対戦するよ」という意味で、結局同じことだよね。だから、表では２つあるけれど、「１つ」として考えるよ。

対戦表の見方に気をつけて、組み合わせを数えると次のようになるよ。

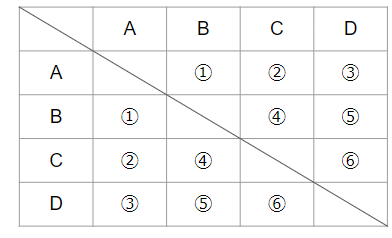
「自分自身と対戦」になってしまうところは数えないので、線を引いてあるね。
そして「A対B」と「B対A」のように同じ組み合わせのところは、同じ数字を書いて、１つ分として数えているよ。

そうすると、数字は➀～⑥までで、全部で６通りの組み合わせがあることがわかるね。

組み合わせについてなんとなくわかったかな？
気をつけなくてはいけないのが、同じ組み合わせを２回数えてしまうこと。
たとえばさっきの問題だったら、こういう風に数えたらだめだよ。

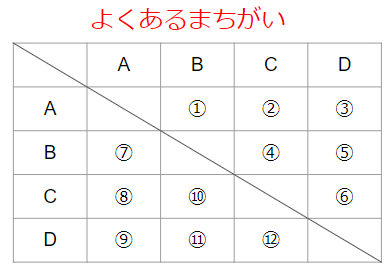
「自分同士と対戦」のところは、ちゃんと線を引いて数えないようにできているけれど、「A対B」と「B対A」のような同じ組み合わせを別のものとして数えてしまっているのが間違いだね。

表で考えることが難しい問題

組み合わせを考えるのに、さっきのように対戦表を使って考えることが難しい場合もあるんだ。

例えば次のような問題。

さっきの問題は「２チーム」を選べばよかったのに対して、今回の問題は「３チーム」を選ばなくてはならないね。

でも対戦表って、縦に１チーム、横に１チームしか書けないから、３つ選ぶとなると立体にするしかなくなっちゃうよね。
それではわけがわからなくなるから、そんな時は図を使って考えてみよう。

組み合わせを図で表して調べてみよう

さっきと同じ問題を今度は図で表して調べてみよう。

組み合わせの問題を解くポイントは「数え忘れがないようにすること」だったよね。

数え忘れがないように、さっきは表で考えたけれど、今度は図（樹形図）で考えるよ。

樹形図で考えるときは、まずはひとつのものを決めて、規則正しく書くことが大切だったね。

数え忘れがないようにするためにまずは「A」について考えてみよう。

Aと対戦できるのって、BとCとDだよね。
図（樹形図）で書いたら次のようになるよ。

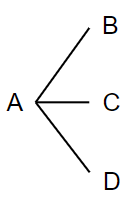
それでは今度は「B」について考えてみよう。

Bと対戦できるのはAとCとDなんだけれど、「BとA」の組み合わせって、「A」について考えたときにすでに出てきた「AとB」と同じことだよね。

だから、「A」を消すよ。

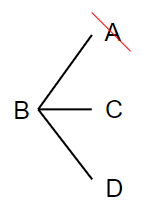
つぎは「C」について考えてみよう。

Cと対戦できるのって、AとBとDなんだけど、
「CとA」って「A」について考えたときの「AとC」と同じだよね。
そして「CとB」ってさっきの「B」について考えたときの「BとC」と同じことだよね。

なので、「A」と「B」を消すよ。

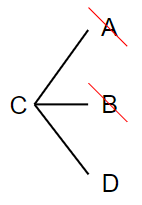
最後に「D」について考えてみよう。

Dと対戦できるのって、AとBとCなんだけど、
「DとA」って「A」について考えたときの「AとD」と同じだよね。
「DとB」って「B」について考えたときの「BとD」と同じだよね。
「DとC」って「C」について考えたときの「CとD」と同じだよね。

だから、「A」「B」「C」を消すよ。

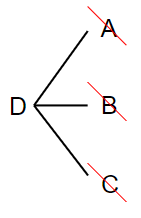
まとめると次のようになるよ。

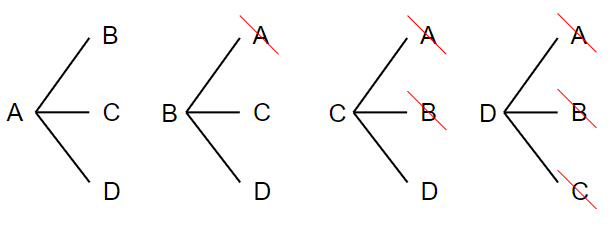
先に出てきたものと同じ組み合わせになってしまうものは、赤線で消してあるね。これらを本当に消して整理すると次のようになるよ。

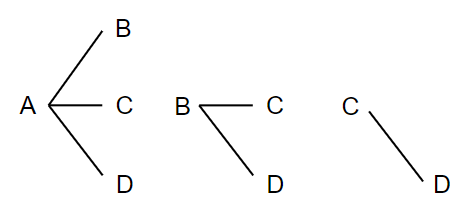
整理された図で数えると、組み合わせは全部で６通りあることがわかるね。

組み合わせを図（樹形図）で書く方法についわかったかな？
図で書くときも、表で考えるときと同じで気をつけなくてはいけないのが、同じ組み合わせを２回数えてしまうことだよ。

組み合わせの練習問題

それでは、組み合わせが何通りあるかを数える問題を実際に解いてみよう。

表で考える場合

さっきの対戦表を
ばなな＝ば、みかん＝み、ぶどう＝ぶ、りんご＝り
として書くと次のようになるよ。

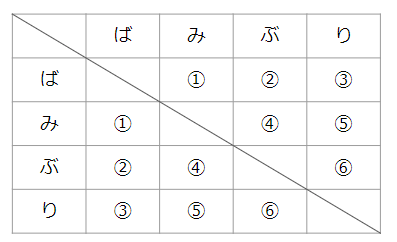
全部で６通りあることがわかるね。

図で考える場合

ばなな＝ば、みかん＝み、ぶどう＝ぶ、りんご＝り
として図（樹形図）を書いてみよう。

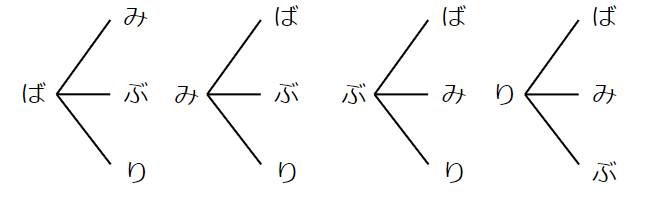
ただ、同じ組み合わせを２回数えてしまっているよね。

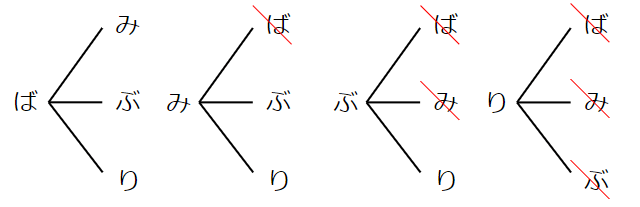
４つから２つを選ぶ組み合わせは６通りだとわかるね。

「組み合わせが何通りあるのか」の求め方まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。