「角錐・円錐・球」とは？（円錐の展開図つき）円柱や角柱との違い
目次
角錐とは
「角錐」っていうのは、ピラミッドを想像したらOK。ピラミッドって先がとがっているよね。先がとがっているものを「錐」っていうんだ。
小学校では、先がとがった形は学習していないよね。
角錐の「角」は、底面が「多角形」であるということ。
例えば、三角形とか、四角形とか、五角形とか。
だから、角錐っていうのは、底面が多角形で先がとがった立体のことをいうよ。
底面の形によって、「○角錐」と名前が変わるよ。
三角錐 四角錐 五角錐
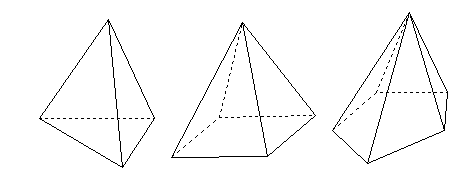
ちょっとおまけの話だけど、「角錐」のことを英語で「pyramid（ピラミッド）」っていうんだよ。
円錐とは
「円錐」っていうのは、次のような立体のことだよ。
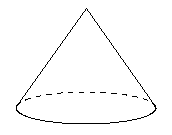
先がとがっていて、底面が円になっているね。
身近な例でいうと、カラーコーンなんかが円錐といえそうだね。ちょっとおまけの話だけど、「円錐」のことを英語で「cone（コーン）」っていうんだよ。
正三角柱と正三角錐のちがい
正三角柱と正三角錐のちがいについて考えよう。ちがいは「柱」か「錐」かだけだね。両方とも底面は「正三角形」なんだけど、「正三角錐」の場合は先がとがっているよ。
正三角柱 正三角錐（先がとがっている）
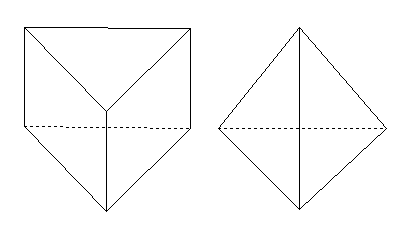
円柱と円錐の違い
円柱と円錐のちがいについて考えよう。両方とも底面は「円」なんだけど、「円錐」の場合は先がとがっているよ。
円柱 円錐
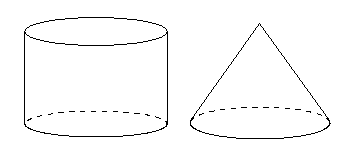
球とは
球っていうのはボールを想像してもらったらOK。つまりどこから見ても丸く見えるものが球だよ。
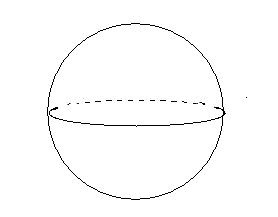
ちょっとおまけの話だけど、「球」のことを英語で「ball（ボール）」っていうんだよ。
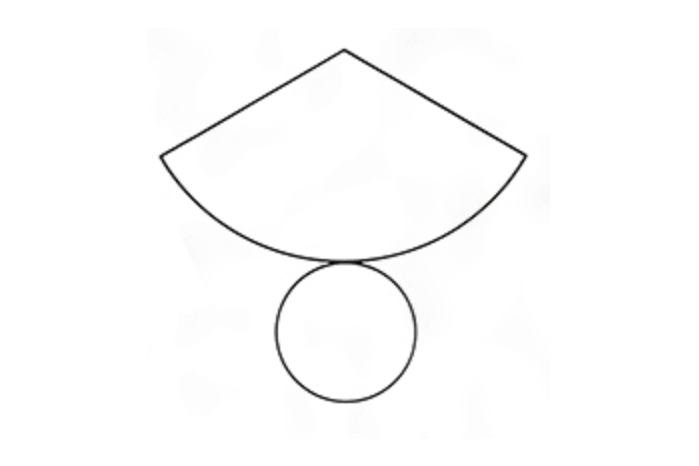
円錐の展開図
円錐の展開図を用意したよ。
ダウンロードして、実際に作ってみよう。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
ご無沙汰してます。また教えてください。
正四角錐の定義についてです。正四角錐に関する問題で、側面の三角形が正三角形であるものも少なくないのですが、正四角錐の定義を見てみると側面が二等辺三角形と書かれたものを見かけます。なぜ底辺が正方形で側面が二等辺三角形または正三角形からなる…….という言い方がされてないのか理由を教えてください。よろしくお願いいたします。