合同とは？「合同な図形の性質」記号を使った表し方を解説

中学２年生の数学で学習する「合同な図形」について、２つの図形が合同であることを、どのように表したら良いのか、表し方のルールや記号の意味、合同な図形がもつ性質をわかりやすく解説するよ。

合同とは？「合同な図形の性質」記号を使った表し方を解説のPDF（5枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

合同な図形とは

小学５年生の算数に登場した、合同な図形について覚えているかな？
中学２年生で習う合同な図形は、小学５年生で習った内容を発展させたものを勉強していくから、小学校の記憶を思い出しながら勉強を進めていこう。

まずは、合同な図形ってどんな図形だったかを振り返っていくよ。

２つの図形がぴったり重なり合うとき、２つの図形は合同というんだったね。

【合同ではない例】
①１か所でも対応する角の大きさや辺の長さが異なるとき

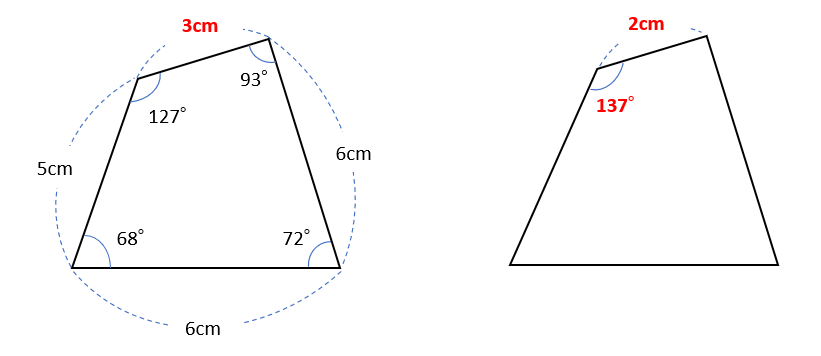
②拡大・縮小の関係になっているとき

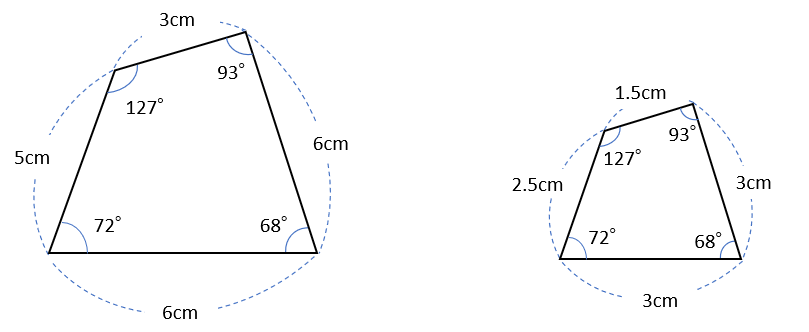
【合同な図形の例】

回転して重なるものは合同といえる

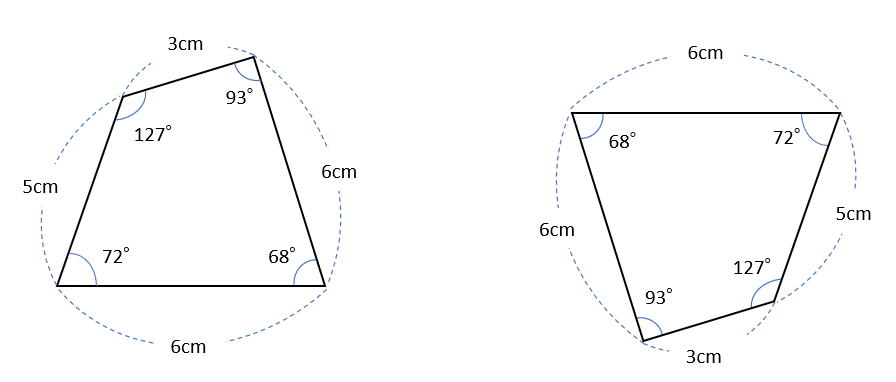
上の図のように、回転させるとぴったり重なるものもあるから、合同な図形を見つける時には注意しよう。

２つの図形が合同であるとき、合同を表す記号『≡』を使うんだ。

四角形ABCDと四角形EFGHが合同で、対応する頂点（合同な図形で重なり合う頂点）が、AとE、BとF、CとG、DとHであるとき、

四角形ABCD≡四角形EFGH

と表すよ。

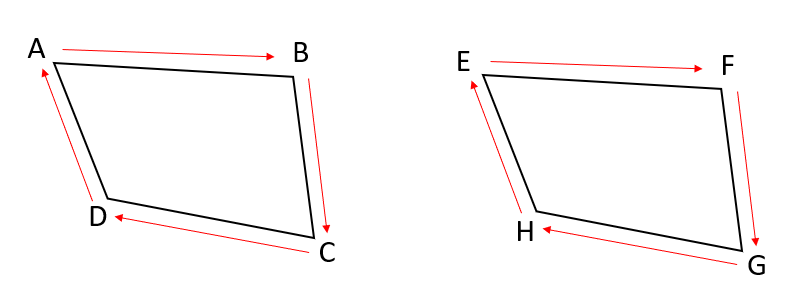
合同を表す記号『≡』を使うときは、上の図のように対応する頂点の名前を周にそって、同じ順に書くから、順番を書き間違えないように注意しよう。

【合同を書き表すときの順番が正しくない例】
①対応する順番になっていないパターン
四角形ABCD≡四角形FGHE
四角形ABCD≡四角形EGFH
※ちなみに、四角形BCDA≡四角形FGHEならば対応順になっているので問題なし！

②対応する順番になっているけれど、周にそっていないパターン
四角形ACBD≡四角形EGFH

角に注目すると対応する順で書きやすくなるから、参考にしてみてね。

合同な図形で、
重なり合う辺のことを「対応する辺」
重なり合う角のことを「対応する角」
といって、合同な図形では対応する辺の長さ・対応する角の大きさはそれぞれ等しくなることを覚えておこう。

例題
次の△ABCと△DEFは合同で、対応する頂点がAとD、BとE、CとFであるとき、
（１）辺ABと対応する辺
（２）∠CABと対応する角
をそれぞれ答えなさい。

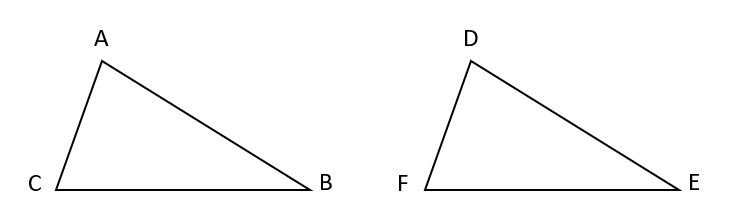
（１）辺ABと対応する辺
辺ABとぴったり重なる辺を見つける問題だね。
図を見れば辺ABと対応する辺は辺DEということがわかるね。

（２）∠CABと対応する角
∠CABとぴったり重なる角を見つけよう。
これも図を参考にすれば、簡単に見つけることができるんだけれども、対応する辺や角を答える時は答えを書く順番にも注意しよう。

今回は∠CABと対応する角を答えるから、∠【Cに対応するF・Aに対応するD・Bに対応するE】の順番で答えるんだ。
だから、答えは∠FDEとなるよ。

今回習った内容は、これから勉強する内容の基礎となるから、忘れないようにしっかりと復習しておこう。

「合同な図形の性質と表し方」まとめ

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。