「平行四辺形の証明」条件ごとの問題と証明の仕方・書き方を解説
中学2年生の数学で学習する「平行四辺形の証明」について、平行四辺形になるための条件を使って、図形が平行四辺形であることを証明する方法をくわしく解説するよ。
2組の対辺がそれぞれ平行である、2組の対辺がそれぞれ等しい、2組の対角がそれぞれ等しい、対角線がそれぞれの中点で交わる、1組の対辺が平行でその長さが等しいという5つの条件ごとの証明問題を紹介しているよ。
応用問題もあるので、ぜひチャレンジして平行四辺形の証明問題に慣れよう!
2組の対辺がそれぞれ平行である条件を使った証明
問題
平行四辺形ABCDで、∠ABCと∠CDAの二等分線と辺BC、辺ADの交点をそれぞれE、Fとするならば、四角形BEDFが平行四辺形であることを証明しなさい。
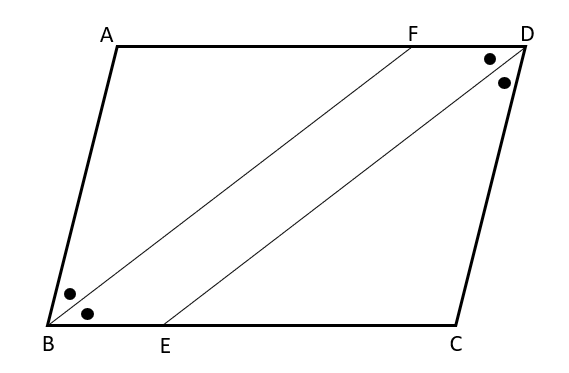
四角形BEDFに関連する角度に注目して、対辺がそれぞれ平行であることを使って、平行四辺形であることを証明していくよ。
(△ABFと△CEDが合同であることを使った方法でも、平行四辺形であることを証明できるよ。)
証明
仮定から、
∠ABF=∠CBF=\(\frac{1}{2}\)∠ABC・・・①
∠ADE=∠CDE=\(\frac{1}{2}\)∠CDA・・・②
平行四辺形の対角はそれぞれ等しいので、
∠ABC=∠CDA・・・③
①、②、③より
∠CBF=∠ADE・・・④
平行四辺形の対辺は平行なのでAD∥BCだから、
FD∥BE・・・⑤
平行線の錯角は等しいので、
∠ADE=∠CED・・・⑥
④、⑥より
∠CBF=∠CED・・・⑦
⑦より同位角が等しいので、
BF∥DE・・・⑧
⑤、⑧より、2組の対辺がそれぞれ平行なので、
四角形BEDFは平行四辺形である。
④、⑥、⑦の求める流れは、下の図を参考にして考えよう。
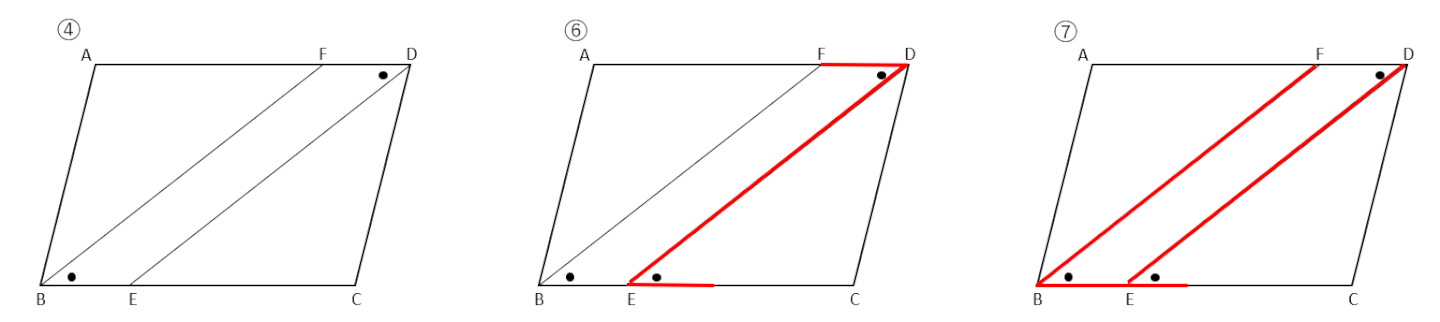
証明を書き始める前に、わかっていることを図にかくことで、どうやって証明したら良いか考えやすくなるよ。
2組の対辺がそれぞれ等しい条件を使った証明
問題
平行四辺形ABCDで、AH=BE=CF=DGならば、四角形EFGHが平行四辺形であることを証明しなさい。
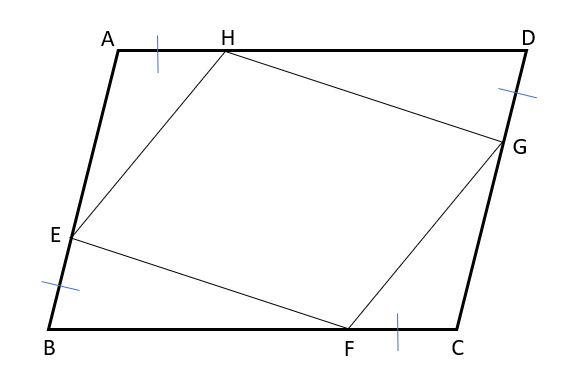
△AEHと△CGF、△BEFと△DGHの合同を証明して、四角形EFGHの対辺がそれぞれ等しいことを使って平行四辺形であることを証明するよ。
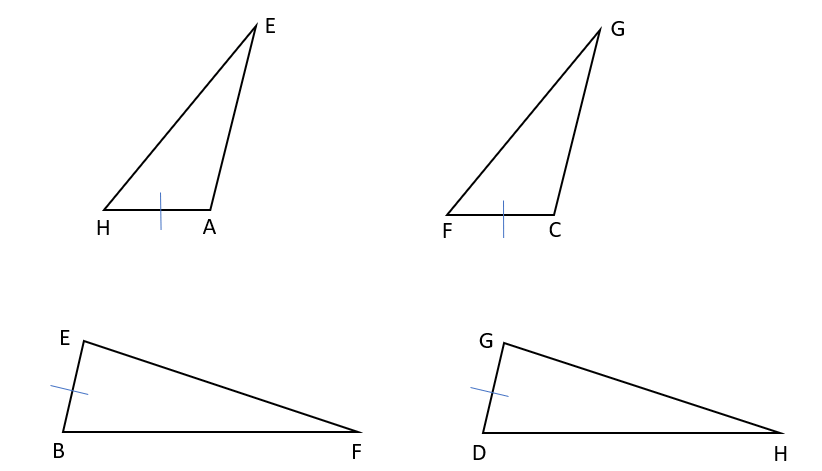
証明
△AEHと△CGFにおいて、
仮定から
AH=CF・・・①
BE=DG・・・②
平行四辺形の対辺は等しいので
AB=CD・・・③
②、③より
AB-BE=CD-DG
AE=CG・・・④
平行四辺形の対角は等しいので
∠HAE=∠FCG・・・⑤
①、④、⑤より2組の辺とその間の角がそれぞれ等しいので、
△AEH≡△CGF
合同な図形の対応する辺は等しいので、
EH=GF・・・⑧
また、△BEFと△DGHにおいても同様にして、
EF=GH・・・⑨
⑧、⑨より2組の向かい合う辺がそれぞれ等しいので、
四角形EFGHは平行四辺形である。
△AEHと△CGF、△BEFと△DGHはそれぞれ同じ手順で証明するから、「同様にして」をうまく使って証明しよう。
2組の対角がそれぞれ等しい条件を使った証明
問題
平行四辺形EBFDで、EA=FC、∠ABC=∠CDAならば、四角形ABCDが平行四辺形となることを証明しなさい。
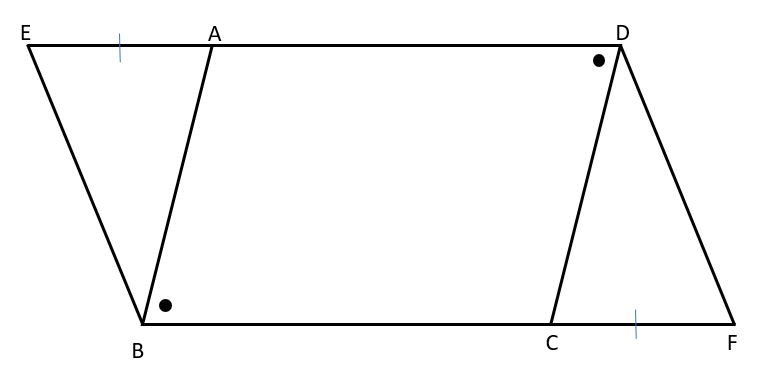
仮定で四角形ABCDの∠ABCと∠CDAが等しいことがわかっているから、2組の対角がそれぞれ等しいことを使って平行四辺形であることを証明するよ。
証明
△ABEと△CDFにおいて
仮定から
AE=CF・・・①
平行四辺形の対辺は等しいので、
BE=DF・・・②
平行四辺形の対角は等しいので、
∠AEB=∠CFD・・・③
①、②、③より
2組の辺とその間の角がそれぞれ等しいので
△ABE≡△CDF
合同な図形の対応する角は等しいので、
∠BAE=∠DCF・・・④
一直線が作る角は180°となるので、
∠BAD=180°-∠BAE・・・⑤
∠BCD=180°-∠DCF・・・⑥
④、⑤、⑥より
∠BAD=∠BCD・・・⑦
仮定から
∠ABC=∠CDA・・・⑧
⑦、⑧より
2組の対角がそれぞれ等しいので
四角形ABCDは平行四辺形である。
∠BADと∠BCDが等しくなる証明(⑤から⑦の部分)については下の図を参考にしながら考えよう。
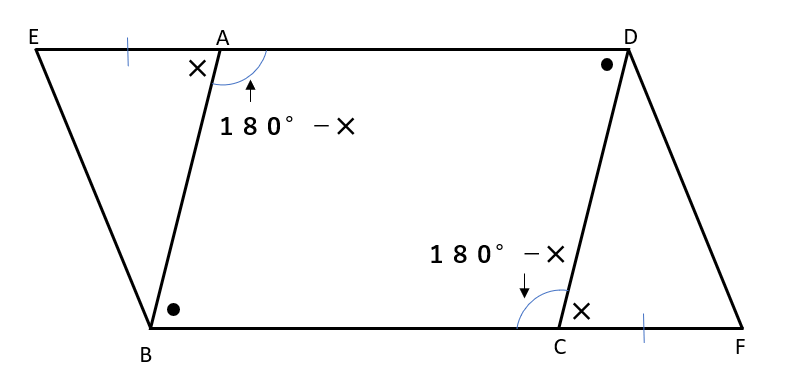
応用問題では、この問題のように「ある角から同じ大きさの角を引いて等しいことを証明する」方法がよく出るから、覚えておこう!
対角線がそれぞれの中点で交わる条件を使った証明
問題
平行四辺形ABCDで対角線BD上にBE=DFとなる点をE、Fとするならば、四角形AECFが平行四辺形となることを証明しなさい。
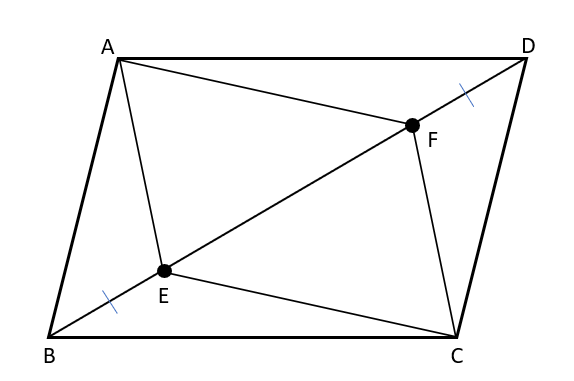
問題の図に対角線BDがあるから、対角線ACも引いた図を使って考えよう。
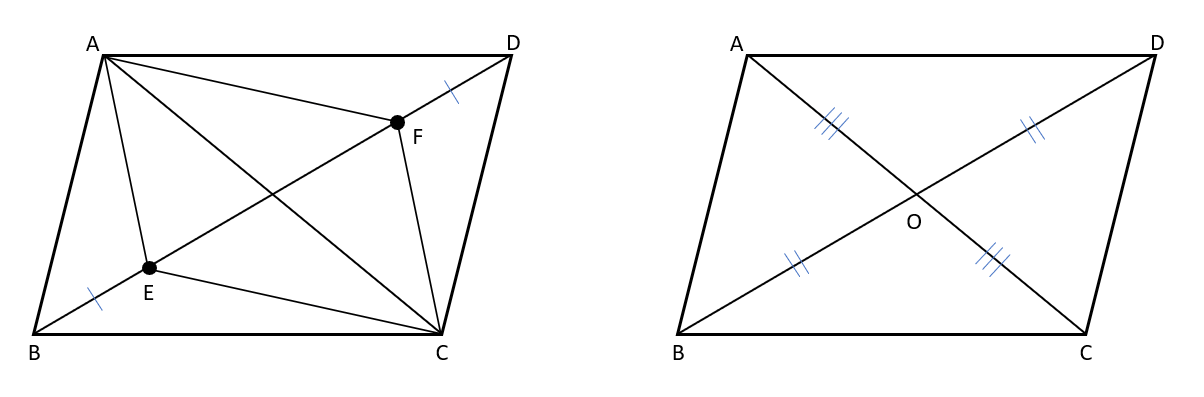
証明
平行四辺形ABCDの対角線の交点をOとする。
平行四辺形の対角線は、それぞれの中点で交わるから
OA=OC・・・①
OB=OD・・・②
仮定から
BE=DF・・・③
②、③から
OB-BE=OD-DF
OE=OF・・・④
①、④より
対角線がそれぞれの中点で交わるから
四角形AECFは平行四辺形である。
平行四辺形になることを証明する問題では、「対角線がそれぞれの中点で交わる条件」がよく使われるよ。
1組の対辺が平行でその長さが等しい条件を使った証明
問題
平行四辺形ABCDでBE=DFとするならば、四角形AECFが平行四辺形となることを証明しなさい。
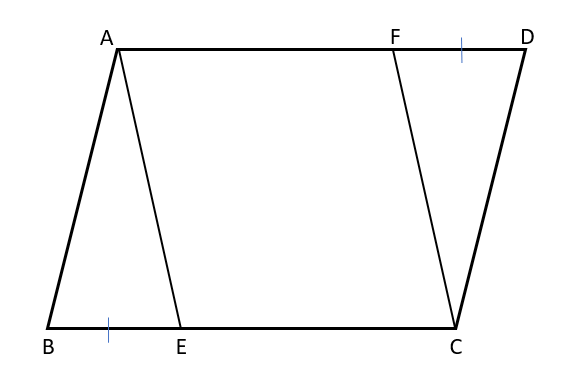
仮定で与えられるBE=DFと平行四辺形の対辺が平行であることを使って証明しよう。
証明
仮定から
BE=DF・・・①
平行四辺形の対辺は等しいので
BC=DA・・・②
①、②より
BC-BE=DA-DF
EC=FA・・・③
平行四辺形の対辺は平行なのでAD∥BCだから
AF∥EC・・・④
③、④より
1組の対辺が平行でその長さが等しいので
四角形AECFは平行四辺形である。
平行四辺形になることを証明する問題では、「1組の対辺が平行でその長さが等しい条件」も使われることが多いよ。
応用問題・難問
これまで勉強したことの総まとめとして、平行四辺形になるための条件を使った応用問題にチャレンジしてみよう!
問題
図のようなAB∥DCである四角形ABCDがあり、辺ADの中点をE、CEの延長とBAの延長との交点をFとするならば、四角形ACDFは平行四辺形になることを証明しなさい。
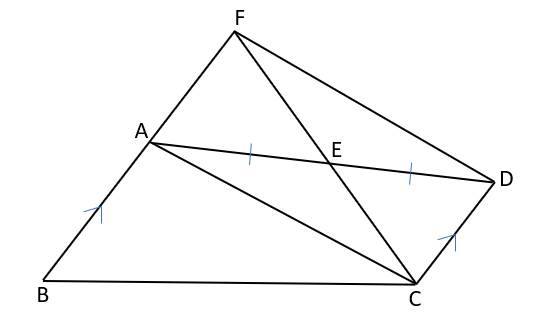
問題文の「辺ADの中点をE」という部分から、対角線がそれぞれの中点で交わることを使って証明することが推測できるね。
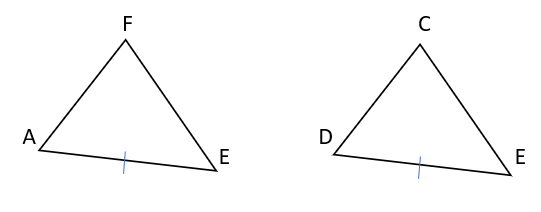
最初に△AEFと△DECが合同であることを証明して、四角形ACDFのもう1つの対角線であるFCの中点がE(FE=CE)であることを証明する手順で解いていこう。
証明
△AEFと△DECにおいて、
仮定から
AE=DE・・・①
対頂角は等しいので
∠AEF=∠DEC・・・②
FB∥DCで平行線の錯角は等しいので
∠EAF=∠EDC・・・③
①、②、③から、1組の辺とその両端の角がそれぞれ等しいので
△AEF≡△DEC
合同な図形の対応する辺は等しいので
FE=CE・・・④
①、④より、対角線がそれぞれの中点で交わるので、
四角形ACDFは平行四辺形である。
平行四辺形になるための条件を使った問題は、入試などでも出題されることがある問題だから、今回紹介した問題を通じて証明問題の解き方をマスターしよう!
また、証明問題は中間点がもらえる可能性があるから、「証明が苦手・・・」という人は、1点でも高い点数を取ることができるように、仮定や図から見てわかることを書いて、解答欄を空欄にせずに粘り強く取り組もう!
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


