単項式と多項式の計算をわかりやすく解説「式の計算」

中学数学で学習する「式の計算」について、「単項式・多項式」とは何か、単項式と単項式の計算の仕方をわかりやすく解説するよ。

単項式と多項式の計算をわかりやすく解説「式の計算」のPDF（10枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

単項式とは

「単項式」とは、「数や文字についての乗法（かけ算）だけで作られた式」のことだよ。

ことばだけだとピンとこないので、どんなものが「単項式」と呼ばれるのか、実際に例を見てみよう。

単項式の例

ｘ
－５
２πｒ
\(\frac{１}{２}\)ａ²
ａ²ｂ

どうかな？
これらの式が、「数や文字をかけただけ」ということがわかるかな？

それぞれの単項式を細かく見てみよう。

ｘ　←文字だけでもOK
－５　←数字だけでもOK
２πｒ（２×π×ｒ）　←数字と文字がかけられているだけ
\(\frac{１}{２}\)ａ²（\(\frac{１}{２}\)ａ×ａ）　←数字は分数でもOK
a²b=a×a×b　　　[文字だけのパターンもある！]

※数字と文字の間に【＋】や【－】が無い式と覚えておこう！

多項式とは

多項式とは、単項式の和（足し算）や差（引き算）の形で表された式のこと

つまり、さっき紹介した「単項式」たちが、足し算や引き算の形になって並んでいる式のことだよ。

多項式の例

ｘ－5
2πr＋\(\frac{１}{２}\) a²
a²b＋2ｘ－5

それぞれの多項式を細かく見てみよう！

ｘ－5　←「文字」と「数字」の引き算の形で表されている
2πr＋\(\frac{１}{２}\) a²　←単項式と単項式の足し算の形で表されている
a²b＋2ｘ－5　←単項式が3つあってもOK！

「項」とは？

多項式を見てみると、いくつかの単項式からできているね。
その単項式のひとつひとつのことを「項」というんだ。
※項は、数字や文字の前についている符号も含むよ！

先ほどの多項式を例に確認してみよう。

ｘ－5 　←項は「ｘ」と「－5」
2πr＋\(\frac{１}{２}\)a² 　←項は「2πr」と「\(\frac{１}{２}\)a²」
※＋は省略してもＯＫ
a²b＋2ｘ－5 　←項は「a²b」と「2ｘ」と「－5」

「次数」とは？

「次数」とは、単項式でかけられている「文字の数」のことだよ。
※「文字の数」という言葉から、「次数」ではなく「字数」と書き間違えてしまう人が多いので注意しよう！

単項式の場合の次数の考え方

単項式の場合の次数

ｘ　←文字の「ｘ」が１つなので、次数は「１」
－5　←数字のみで文字がないので、次数は「０」
2πr　←「π」と「r」という文字が２つなので、次数は「２」
\(\frac{１}{２}\)a²　←「a²」は、「a×a」と分けて考えると2つあるので、文字「a」が２つなので、次数は「２」
a²b　←「a²b」は、「a×a×b」と分けて考えると3つあるので、文字「a」が２つ、文字「b」が１つで合計３つなので、次数は「３」

多項式の場合の次数の考え方

多項式の場合、次数の考え方には注意が必要だよ。
なぜなら、多項式の中の「各項のもっとも大きいものが多項式の次数となる」からなんだ。

つまり、「合計」ではなくて、「代表」のイメージ。
各項の次数を合計するのではなくて、その多項式の中で一番次数が大きいものが、代表となるということなんだ。

多項式の場合の次数

ｘ－5 　←次数は「１」
（項と次数：「ｘ」の次数は１、「－5」の次数は０）
2πr＋\(\frac{１}{２}\)a²　←次数は「２」
（項と次数：「2πr」の次数は２、「\(\frac{１}{２}\)a²」の次数も２で、どちらも同じ次数２なのでそのまま２となる）
a²b＋2ｘ－5　←次数は２
（項と次数：「a²b」の次数は３、「2ｘ」の次数は１、「－5」の次数は０で、一番大きい次数は「a²b」の次数「３」なので、この多項式の次数は「３」となる。）

各項の、次数同士を足し算しないように注意しようね。

また、次数が１の多項式を「１次式」、次数が２の多項式を「２次式」、次数が３の多項式を「３次式」というよ。

これまで学習してきた「一次方程式」とか「一次関数」とかの「一次」は、その方程式や関数の式が「１次式」だからそう呼ばれていたんだね。

多項式の加法（たし算)

多項式の加法（足し算）の計算の仕方について確認しよう。

まず、多項式の加法には、絶対に守らなければならないルールがあるんだ。

それは「文字が同じ項でしか計算できない」というルール。

中学１年生の時に学習した、一次方程式を振り返ってみよう。

－2ｘ＋3＋3ｘ＋2=2

この方程式を解く時、「ｘがついている項」と「数字のみの項」を一緒に計算してはいけなかったよね。

実際に計算してみると・・

－2ｘ＋3ｘ＋3＋2=2
ｘ＋5=2
ｘ=2－5
ｘ=－3

このように計算したよね。

多項式の計算でも、同じように計算していくんだ。

例：5ｘ＋2y－3ｘ－5yを計算してよう

①同じ文字同士をまとめやすくするために並べかえる

5ｘ－3ｘ＋2y－5y

②方程式と同じように、同じ文字がついている項同士で計算していく。

5 ｘ－3ｘ＋2y－5y
2ｘ－3y

例：5ｘ²－3ｘ＋8ｘ－2ｘ²を計算してみよう！

先ほどの例題と同じ手順で・・と思ったものの、『全部ｘが含まれている』と手が止まってしまうかもしれないね。

文字はｘのみが使われているけれど、ｘとｘ²は「別なもの」なので注意が必要だよ！

では早速解いてみよう。

①同じ文字同士をまとめやすくするために並べかえる

5ｘ²－2ｘ²－3ｘ＋8ｘ

②ｘ²とｘを分けて項同士で計算していく。

5ｘ²－2ｘ²－3ｘ＋8ｘ

3ｘ²＋5ｘ

多項式の減法（引き算）

多項式の減法（引き算）の計算の仕方について確認しよう。

多項式の減法も加法と同様に、「文字が同じ項でしか計算できない」というルールを守って、解いていけば大丈夫。

例：（3ｘ＋2y）－（－4ｘ＋4y）を計算してみよう！

①まず、（　　）を外そう。
「－」は分配法則を使って計算することを忘れないでね。

3ｘ＋2y＋4ｘ－4y

②加法の時と同じように、同じ文字同士をまとめやすくするために並べかえる

3ｘ＋4ｘ＋2y－4y

③同じ文字がついている項同士で計算していく

3ｘ＋4ｘ＋2y－4y
7ｘ－2y

実際に計算してみるとわかる通り、減法は最初の（　　　）を外すところ以外は、加法の計算手順と同じだね。
あとは計算ミスをしないように注意しながら解き進めていけば心配することはないよ。

多項式の加法・減法の筆算問題

多項式の加法・減法では、筆算の形式で解く問題が出題されるよ。

加法・減法ともにルールを守って計算すれば間違えることはないので、しっかりとマスターしていこう！

多項式の加法の筆算

例：（3ｘ－2y）＋（4ｘ＋5y）を筆算で計算してみよう！

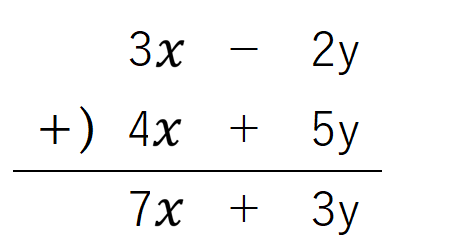
同じ文字どうし、そのまま足し算をすればOKだよ。
　３ｘ＋４ｘ＝７ｘ
　－２ｙ＋５ｙ＝３ｙ

多項式の減法の筆算

例：（3ｘ－2y）－（4ｘ＋5y）を筆算で計算してみよう！

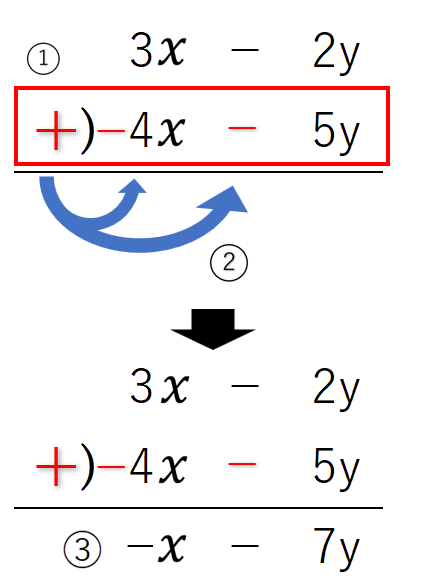
引き算の筆算をするときは、

➀引き算を足し算に変える

➁足し算に変えたら、符号を変える（＋は－に、－は＋に）
　※上の段は、変えずにそのままにしよう

③符号を変えたら、足し算の時と同じように計算するよ。

【やや難】多項式の加法・減法の分数を含む計算

多項式の加法・減法の計算問題では、分数を含む問題も出題されるよ。
分数を含む問題では、多くの人がミスしやすい箇所があるんだ。
その点に注意しながら、多項式の加法・減法を完璧にマスターしよう！

例：2ｘ＋3ｙ－\(\frac{2}{3}\)ｘ＋2ｙを計算してみよう！

どうやって計算すればいいだろう？

たろう

分数があるから、まずは全部に３をかけて、分数をなくせばいいんじゃないかな。

くまごろう

実は、この解き方は間違いなんだ。多くの人がこのミスをしてしまうので、要注意！！

先ほどのように、『〇をかけて』という解き方をしていいのは、方程式の時だけなんだ。

では、この式と方程式では何が違うのかな？

それは式の中に「＝」があるかないか、という違いだけだよ。

実際に見比べてみよう。

方程式：－2ｘ＋3＋3ｘ＋2=2
↑「＝」がある式なので、式全体に数字をかけてもOK！

多項式の計算：2ｘ＋3ｙ－\(\frac{2}{3}\)ｘ＋2ｙ
↑「＝」がない式なので、式全体に数字をかけるのはNG！

この違いに注意しようね。

では、今回の多項式の計算について確認していくよ。

①同じ文字同士をまとめやすくするために並べかえる（分数がない計算と一緒だね）

2ｘ－\(\frac{2}{3}\)ｘ＋3y＋2ｙ

②分数がついている文字は、通分（分母をそろえる）をして計算できるようにする

\(\frac{6}{3}\)ｘ－\(\frac{2}{3}\)ｘ＋3y＋2ｙ