「一次関数」とは?日常生活の例をもとにxとyの関係を式で表そう
中学数学で学習する「一次関数」について、「χとyの関係を式で表す」とはどういうことか、日常生活の中の一次関数を紹介しながらわかりやすく解説するよ。
スタートが0ではない「χとyの関係」を式で表してみよう
「χとyの関係を式で表す」とは、「χ」と「y」というある数があるときに、「xがいくつになる」と「yはいくつになる」というように、χとyそれぞれが、もう片方の数によって変わるような関係だとするよ。
そういう関係の時、それを「式で表してみよう」ということだよね。
では、実際に「片方の数によってもう片方の数が変わるような関係」を例にみながら、考えてみよう。
例題
(1)太郎くんは、毎月200円ずつ貯金をしています。貯金をしはじめてからχヶ月後の貯金額をy円として、χとyの関係式を表してみよう。
(2)太郎くんが最初に1600円持っていて、毎月200円ずつ貯金をした場合、貯金をしはじめてからχヶ月後の貯金額y円の関係はどうなりますか。χとyの関係式を表してみよう。
毎月200円ずつ貯金をする場合、貯金をした月数(何ヶ月貯金をしたのか)と、貯金できた額は関係があるよね。
それがどういう関係かを表す式を考えれば良いということだね。
(1)まずは、月々にお金がたまっていく様子を表にしてみよう。
上が「何ヶ月貯金をしたのか」、下が「いくら貯金できたのか」だね。
| χヶ月後 | 0(スタート) | 1 | 2 | 3 | 4 |
| y円 | 0 | 200 | 400 | 600 | 800 |
この表を見ると、小学生や中学1年生の時に習った「比例」だということに気づくかな?
グラフでも表してみるよ。
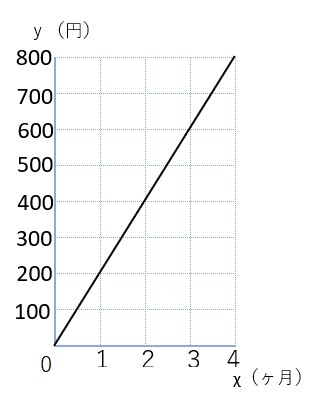
グラフは原点を通る直線になったね。
やっぱり比例の関係だということがわかるね。
あとは、このグラフを式に表すと
y=200χ
となったね!
これで、「χとyの関係を式で表す」ことができたね。
比例の式の求め方(復習)
比例の式の求め方を忘れてしまった人はここで確認しておこう。
比例の式は
y= aχ
と表すことができたね。
そして、aには「比例定数」という名前がついていたね。
そして、yとχに値を代入してaを求める方法で式を求めることができるよ。
今回は、上の表の「χ=1のとき、y=200」を代入すると
a=200
になって、y=200χを求めることができるよ。
また、a=200については、
χが1増えるとyが200ずつ増えている
という関係からも求めることができたね。
※χの値が1増えるときに、対応するyの値がどのくらい増えたり減ったりしているかを表すものが比例定数だよ。
比例についてちゃんと思い出せたか不安な人は、「比例の式の求め方を解説しているページ」もチェックしてね!
(2)次の問題は、最初から1600円持っているところからスタートする問題だね。
(1)の問題と同じように、まずは表を書いて考えてみよう。
違うところは、「スタート」のところで、すでにy(貯金できた額)は1600(円)になっているところだよ。
| χヶ月後 | 0(スタート) | 1 | 2 | 3 | 4 |
| y円 | 1600 | 1800 | 2000 | 2200 | 2400 |
次にこの表からグラフを描いてみよう。
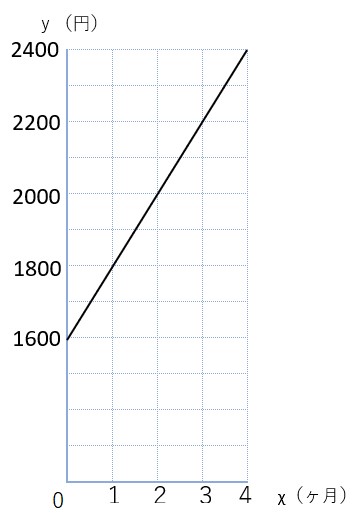
(1)で描いたグラフと見比べてみると、スタートの位置が原点ではなくて、yが1600のところから始まっているだけで、すごく似ていることに気が付くかな?
求める式も(1)と似ていて、スタートの位置の分(χ=0の時のyの値。今回なら、1600だね。)を(1)の式に加えてあげればOKなんだ。
(1)の式は、y=200χ だったね。
ここに、「1600」を加えてあげればいいんだよ。
というわけで、(2)の関係を表す式は
y=200χ+1600
となるんだ。
どうして(1)の式に「1600」を加えてあげればいいだけなの?
今回、貯金をする月の数(χ)と、毎月貯金する金額(200)は、(1)も(2)も同じだよね。
ということは、貯金した額(y)は、同じく貯金した月数(χ)と毎月の貯金額(200)をかけたものになるから、やっぱりy=200xで変わりがないんだ。
これが、(1)の式とおなじで良いと言った理由だよ。
ただ、ここに、スタートのときからある「1600」を足してあげなきゃいけないよね。
それが、(1)の式に、1600を足せば良いと言った理由だよ。
つまり、χとyの関係はもともとは比例の関係なので、y=aχで良いんだけれど、スタートの時の数値が「0」ではないので、その数分を足す必要があるんだね。
そうだね。ただ、この「スタートのときの数値」を毎回こういうふうに言っていたら大変なので、アルファベット「b」であらわすよ。
このように、「yとχは本当なら比例の関係なんだけれど、スタートが0ではなくbから始まるよ」という関係を、式では
y=aχ+b
とあらわすんだ。
そして、この式の形で表される関係のことを、今回学習する「一次関数」と呼ぶんだよ。
1次関数とは
「1次関数」なんてことばだけ見ると、なんだか難しそうだなぁってなってしまうよね。
でも、安心してね。ことばの意味をくわしく説明するよ。
「関数」とは、「ある数と、ある数が関係しているよ」という意味だったよね。
今回で言えば、「貯金した月の数と、貯金できた金額」は関係があるよね。
これが「関数」。
では、「1次」は何かというと、中学数学では、数だけではなく「文字」が登場しているよね。
この「文字」が、「いくつかけられているか」が「次数」なんだよ。
さっきの式をもう一度確認してみよう。
y=200χ+1600
この式には、「y」と「χ」という文字が登場しているね。
この文字たち、「それぞれいくつかけられているかな?」
yは見えない「1」とかけられているよ。「y」がひとつだけかけられているね。
χは「200」とかけられているよ。「χ」がひとつだけかけられているね。
なので、この式は「文字がひとつだけかけられている」式なんだ。
yとχ、それぞれひとつかけられているから、「2つかけられている」と思ってしまうかもしれないけれど、この「次数」は、「全部でいくつ」かではなくて、「最高でいくつ」で考えるんだよ。
yとχ、それぞれ「ひとつかけられている」ので、結局この式の中での最高は「ひとつ」なんだ。
かけられている数が最高「1」の、関係が数の式なので、
「一次関数」と呼ぶというわけだね。
定数とは
一次関数についてはわかったかな?
ところで、今回の一次関数の式
y=200χ+1600
だけれど、この「200」と「1600」は、ケースによってで数字が変わるよね。
たとえば、もし「毎月400円貯金する」だったら
y=400χ+1600
になるし、
もし「スタートは2000円」だったら
y=200χ+2000
になるよね。
どんな数がくるかは、ケースによって違うので、これを文字におきかえて式を表すんだ。
「χの値が1増えるときに、対応するyの値がどのくらい増えたり減ったりしているかを表すもの」を「a」と表して、
「スタートの位置の分(χ=0の時のyの値)」を「b」と表すんだ。
そうすると、式は
y=aχ+b
となるよ。
aは比例と同じようにχの値が1増えるときに、対応するyの値がどのくらい増えたり減ったりしているかを表す「比例定数」だね。
bは、比例にはなかったもので「定数」と呼ばれるよ。
問題によっては、プラスの時もマイナスの時もあるんだ。
(もし、「借金がある状態から貯金をする」というケースだったら、「b」はマイナスになるよね。)
余裕があったら読もう!
「比例は一次関数の仲間だった!」
y=aχ+bの一次関数で、
b=0の時にできる特別な式
y=aχ
のことを中学1年生で習った比例っていうんだよ。
つまり比例は一次関数の仲間なんだ。
一次関数のグラフの形は、さっきも登場したように比例と同じように右上がりや右下がりの直線になるよ。
ただし、比例と違って「b」があるので、原点(0,0)を通らないことがポイントだよ。
もし原点を通るなら、それは「比例」になるということだね。
一次関数「y=aχ+b」とは?まとめ
- 一次関数とは、「文字がひとつだけかけられている」「関数」の式のことで、y=200χ+1600のような式のことをいう。
- χの値が1増えるときに、対応するyの値がどのくらい増えたり減ったりしているかを表すものを「比例定数」といい、「a」であらわす。
- χ=0の時のyの値を「定数」といい、「b」と表す
- y=aχの「比例」は、一次関数の仲間で、「b=0」の場合の式。
日常生活の中の一次関数を探そう
一次関数をもっとよく理解するために、身のまわりの出来事で一次関数で表すことができるものを探してみよう。
問題
次の中で一次関数の式で表されるものがどれか選びなさい。
また、全ての問題についてyをχの式で表しなさい。
(ア)25℃の水を温めるとき、1分間につき2℃ずつ水の温度が上がります。χ分後の水の温度をy℃とするときの関係式
(イ)1辺がχcmの正方形の周の長さycmの関係式
(ウ)20個のリンゴをχ人で分けた時の1人あたりの個数y個の関係式
(エ)1000円を持って、50円のお菓子をχ個買った時の残金y円の関係式
まずは、それぞれの式がどういったものになるか考えてみよう!
ただ、どうしてもすぐに求めることが難しいという場合には、次の手順で考えてみよう。
χとyの関係式を考える時の手順
① χとyの表を作る
② χとyのグラフを描く
③ ①と②を参考に式を考える
(ア)
上の手順通りに考えてみよう。
① χとyの表を作る
| 温めた時間χ(分後) | 0 | 1 | 2 | 3 | 4 |
| 水の温度y(℃) | 25 | 27 | 29 | 31 | 33 |
② グラフを描く
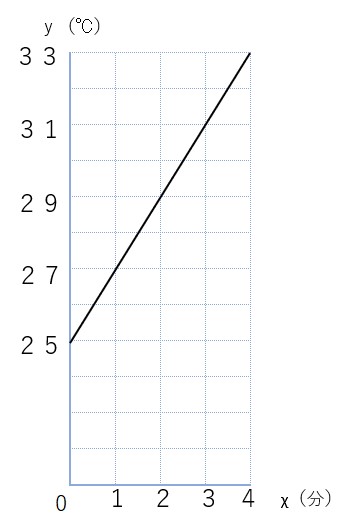
③ ①と②を参考に式を考える
表やグラフの形から、y=aχ+bの形で表すことができそうだね。
χが1増えると、yが2ずつ増えている⇒a=2
χが0の時のyの値が25⇒b=25
以上のことから、
y=2χ+25
と表すことができて、一次関数といえることもわかったね。
(イ)
①χとyの表を作る
正方形の周の長さは、4つの辺を全て足した長さのことだよ。
正方形は4つの辺が全て同じ長さだから、
周の長さ=1辺の長さ×4
と計算してOKだよ。
| 正方形の1辺の長さχ(cm) | 0 | 1 | 2 | 3 | 4 |
| 正方形の周の長さy(cm) | 0 | 4 | 8 | 12 | 16 |
②グラフを描く
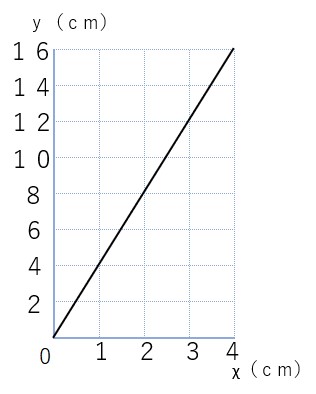
③ ①と②を参考に式を考える
グラフを見てわかる通り、これは比例のy=aχの形になることがわかるね!
χが1増えると、yが4増えているから、a=4になるので
y=4χ
と表すことができるね。
これは比例の式だけれども、比例も一次関数の仲間だから、(イ)も一次関数といえるよ。
(ウ)
①χとyの表を作る
| 分けた人数χ(人) | 1 | 2 | 4 | 5 | 10 |
| 1人あたりの個数y(個) | 20 | 10 | 5 | 4 | 2 |
χの3や6を飛ばしているのは、その人数だとうまく分けることができないからだよ。
②グラフを描く
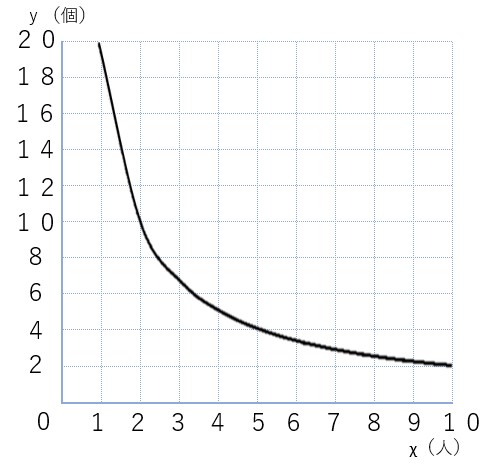
③ ①と②を参考に式を考える
グラフの形から、反比例の式だということがわかるね。
反比例の式は
y=\(\frac{a}{χ}\)
で表すことができたね。
また、反比例のaは
a=χ×y
で求めることができるよ。
※グラフのχとyをそれぞれ掛けてみると、全て20になっているよ。
以上のことから、今回求める式は
y=\(\frac{20}{χ}\)
となり、一次関数ではないことがわかったね。
(エ)
①χとyの表を作る
| お菓子の個数χ(個) | 0 | 1 | 2 | 3 | 4 |
| 残金y(円) | 1000 | 950 | 900 | 850 | 800 |
②グラフを描く
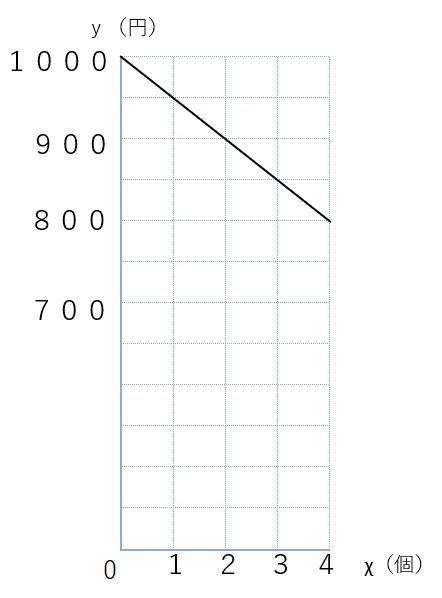
③ ①と②を参考に式を考える
グラフの形から、y=aχ+bの形で表すことができそうだね。
χが1増えると、yが50ずつ減っている⇒a=-50
χが0の時のyの値が1000⇒b=1000
以上のことから、
y=-50χ+1000
と表すことができて、一次関数といえることもわかったね。
答え
一次関数の式で表されるもの(ア)(イ)(エ)
それぞれの式
(ア)y=2χ+25
(イ)y=4χ
(ウ)y=\(\frac{20}{χ}\)
(エ)y=-50χ+1000
「一次関数」まとめ
一次関数や比例、反比例については
①χとyの表を書く
②χとyのグラフを描く
③関係を式に表す
この手順で確認すると、見分けることができるよ。
繰り返し手順通りに確認を続けることで、文章を見ただけでどの式かわかるようになるから、コツコツ取り組んでいこう。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

-
ありがとうございました!




とてもわかりやすかった