二等辺三角形になる条件「二等辺三角形の証明」(逆と反例とは?)
中学2年生の数学で学習する「二等辺三角形になるための条件」について、二等辺三角形になるためにはどんな条件が必要なのか?を「逆」と「反例」の考え方を解説しながら説明するよ。
二等辺三角形になる条件を確認して、「二等辺三角形の証明(二等辺三角形であることを証明する問題)」の解き方をくわしく解説していくよ。
- 「二等辺三角形の底角は等しい」と、
- 「二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する」
という二等辺三角形の性質(定理)を紹介したよね。
つまり、今みんなが認識しているのは、
- 「二等辺三角形である」→ということは→「底角は等しい」。
- 「二等辺三角形である」→ということは→「頂角の二等分線は、底辺を垂直に2等分する」。
ということだよね。
今回学習するのは、ズバリ「それって、逆もOKなのかな?」ということ。
つまり、
- 「底角が等しい」→ということは→「二等辺三角形である」とか、
- 「頂角の二等分線が、底辺を垂直に2等分する」→ということは→「二等辺三角形である」
というのが、OKなのかどうか?ということだね。
これについて確かめるために、2つの数学用語「逆」と「反例」ということばをまず紹介するね。
「逆」とは
まず、「逆」について確認しよう。
逆とは、あることがらの仮定と結論を入れかえたもの
どうだろう、ピンとくるかな?
たとえば、「インドカレー」って、「辛い」よね。
これを、「インドカレー」ならば(仮定)、それは「辛い」(結論)というように考えてみよう。
そうすると、「逆」とは、あることがらの仮定と結論を入れかえたものだったよね。
ということは、入れかえると「辛い」ならば、それは「インドカレー」である、となるね。
どうかな?これって正解だろうか?
結論から言うと、「辛い」からって、「インドカレー」だとは限らないよね。
だから、これは正しいとは言えないね。
数学の「逆」とは、このように、あることがらについて「仮定」と「結論」があったときに、それを入れかえてもOKかどうか?ということを考えることなんだよ。
では、実際に数学の例題で「逆」を考えてみよう。
例題
χ≧3ならばχ>1の逆を答えなさい。
この問題の仮定はχ≧3、結論はχ>1だから
この問題の逆は、χ>1ならばχ≧3
ということがわかるね。
では、この「逆」はOKなのか?
これも「インドカレー」の例と同じように、今回の例題の逆は、成り立たない場合があるんだ。
例えば、χ=2の時を考えよう。
χ>1には当てはまるけれども、χ≧3には当てはまらないよね。
インドカレーや今回の例題のように、逆の内容は、必ず正しいというわけではないから確認する必要があるんだね。
「反例」とは
では、「反例」とはどういうことか確認しよう。
反例とは、あることがらが成り立たない例のこと
これは、さっき説明した「逆」とセットで使うことが多いんだ。
たとえば、さっきのインドカレーの例をもう一度考えるよ。
太郎くんが
「インドカレーって、辛いよね。だから、辛いものっていったら、それって絶対インドカレーだよね。」
と言っていたとする。
それに対して、友達が「そうとは限らないでしょ」と反論したとするよ。
でも、太郎くんからしたら「そうとは限らない」なんて言葉だけで納得できるかな?
なんとなくモヤモヤするよね。
これをもし「キムチだって辛いけど、インドカレーじゃないでしょ」と反論されたらどうだろう。
これはもう「た、たしかに・・・!」と納得するしかないよね。
これが、「反例」だよ。
「辛い→インドカレー」ということがらが成り立たないように、反証(そうならないことの証明)となる例ということだね。
数学で、「逆」が成り立つのかどうかを確認するとき、成り立たないことを証明するためには「反例」を答えるんだよ。
ではさっきの例題で確かめてみよう。
例題の逆「χ>1ならばχ≧3」は、当てはまらない「χ=2」という例があったよね。
これが、今回説明した「反例」ということだよ。
それでは、逆と反例に関する問題にチャレンジしてみよう。
問題
次の(1)(2)について、それぞれの逆をいいなさい。また、それが正しいか正しくないかもいい、正しくない場合には反例も答えなさい。
(1) χ=1、y=2ならばχ+y=3
(2)2つの三角形が合同ならば、面積は等しい
(1)
まずは問題の仮定と結論を確認しよう。
仮定 χ=1、y=2
結論 χ+y=3
逆は、この仮定と結論を入れかえたものだから
χ+y=3ならばχ=1、y=2
これは「正しくない」が正解だね。
反例は、χ=3、y=0(その他にも、χ=-2、y=5など、複数あるよ)
(2)
(1)と同じように問題の仮定と結論を確認しよう。
仮定 2つの三角形が合同
結論 面積は等しい
逆は、この仮定と結論を入れかたえものだから
面積が等しいならば、2つの三角形は合同である。
これは正しいように見えるけれど、「正しくない」が正解だよ。
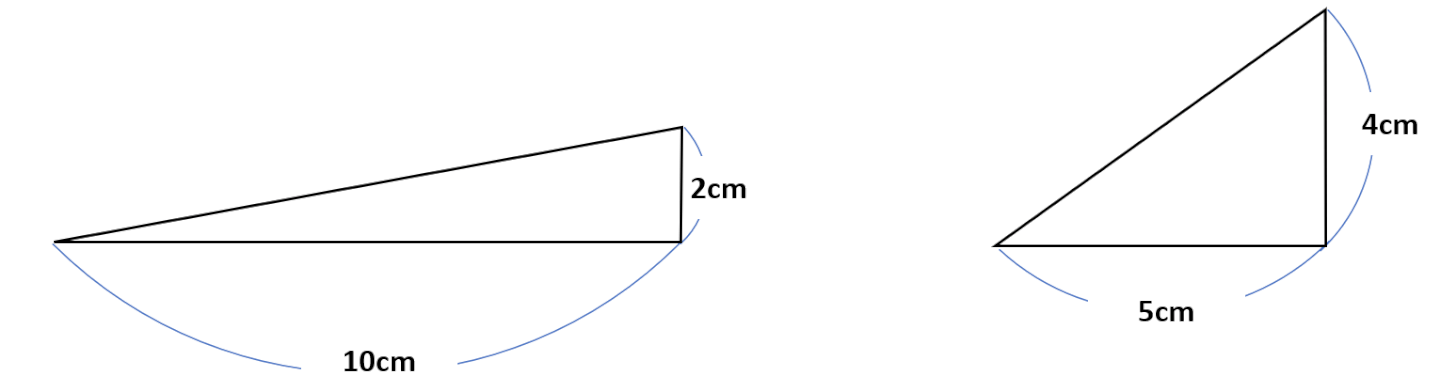
反例は、底辺が10cm、高さが2cmの三角形と底辺が5cm、高さが4cmの2つの三角形
上の問題のように定期試験では、「逆」を答え、その内容が正しいか正しくないかを確認して、正しくない場合には「反例」を答えるという問題が出題されるときがあるから、言葉の意味も忘れずに覚えておこう!
二等辺三角形になるための条件を確かめよう
さて、「逆」と「反例」とはなにかがわかったら、いよいよその考え方を使って、「二等辺三角形になるためには、どんな条件があるのか?」を確認してみよう。
どうやって確認するのかというと、最初に少し説明したとおり、
今は「二等辺三角形である(仮定)ならば、底角は等しい(結論)」が正しいことはわかっているよね。
同じく、「二等辺三角形である(仮定)ならば、頂角の二等分線は、底辺を垂直に2等分する」も正しいとわかっているよね。
この2つの「逆」が正しいかどうかを考えるんだ。
この2つの「逆」が正しいのであれば、
- 「底角が等しい(仮定)ならば、二等辺三角形である(結論)」と
- 「頂角の二等分線が、底辺を垂直に2等分する(仮定)ならば、二等辺三角形である(結論)」
ということができるよね。
そう、これが「二等辺三角形になるための条件」になるということなんだ。
では、それぞれが正しいかどうかを証明してみるよ。
底角が等しい(仮定)ならば、二等辺三角形である(結論)の証明
三角形ABCがあって、底角BとCがひとしいとするよ。
そして、頂角Aの二等分線をひいて、底辺BCとの交点をDとするよ。
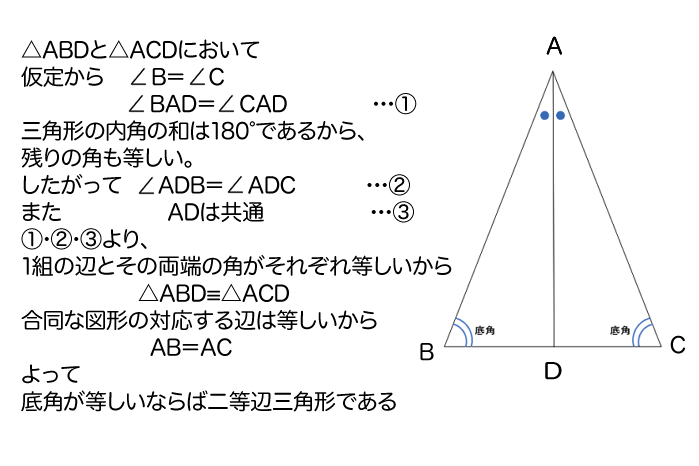
「底角が等しいならば、二等辺三角形である」を証明することができたね。
ということは、「底角が等しい」は、「二等辺三角形になるための条件」の1つとして正しいということだね。
頂角の二等分線が、底辺を垂直に2等分する(仮定)ならば、二等辺三角形である(結論)の証明
まず、三角形ABCがあって、頂角Aの二等分線が、底辺BCを垂直に二等分するとするよ。
そして、その二等分線と底辺BCの交点をDとするよ。
「頂角の二等分線が、底辺を垂直に2等分する(仮定)ならば、二等辺三角形である(結論)」の証明
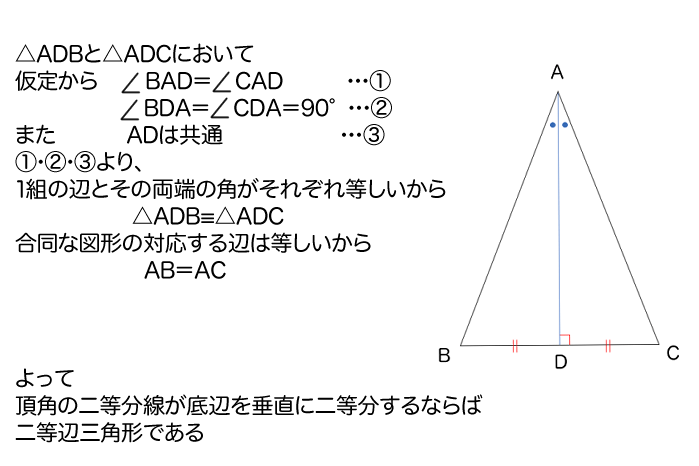
「頂角の二等分線が、底辺を垂直に2等分する(仮定)ならば、二等辺三角形である(結論)」を証明することができたね。
ということは、「頂角の二等分線が、底辺を垂直に2等分する」は、「二等辺三角形になるための条件」の1つとして正しいということだね。
二等辺三角形になるための条件
三角形が二等辺三角形になるための条件は、これまでに確認してきた「定義」や「定理」、そして二等辺三角形の性質の逆が正しいと証明できたものをまとめて、次のとおりになるよ。
二等辺三角形になるための条件
- 2つの辺が等しい時(二等辺三角形の定理だね)
- 2つの角が等しい時(底角が等しい=2つの角が等しいと同じだね)
- 頂角の二等分線が、底辺の垂直二等分線と一致する時(つまり、頂角の二等分線が底辺を垂直に2等分するということだね)
上の3つの中でも特に「2つの角が等しい」という条件は、テストなどでもよく出てくるから、忘れないように覚えておこう!
実際の問題を使って、これら「二等辺三角形になるための条件」を使ってどのように「ある三角形が、二等辺三角形である」ということを証明していくかを見ていこう。
例題
下の図で△ABCはAB=ACの二等辺三角形で、∠ABC、∠ACBのそれぞれの二等分線を引き交点をPとするならば、△PBCが二等辺三角形になることを証明しなさい。
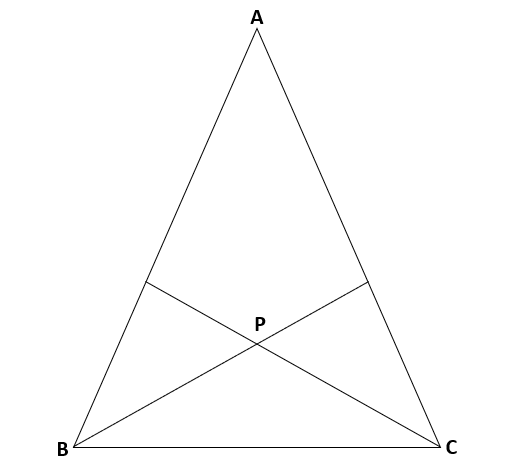
①仮定と結論を問題文から見つけよう。
仮定
△ABCがAB=ACの二等辺三角形、∠ABCと△ACBのそれぞれの二等分線を引いた交点がP
結論
△PBCが二等辺三角形
②仮定からわかることを書こう。
この問題の仮定からわかることは、複数あることに気づけたかな?
△ABCが二等辺三角形だから、∠ABC=∠ACB
(AB=ACも仮定からわかるけれど、証明に使わないから省略しているよ)
BP、CPが∠ABCと∠ACBの二等分線になるから、∠CBP=\(\frac{1}{2}\)∠ABC、∠BCP=\(\frac{1}{2}\)∠ACB
ここまでの内容を使って証明していくよ。
※合同を証明する問題ではないから合同条件も登場しないから注意しよう。
例題の証明
△PBCにおいて
二等辺三角形の底角は等しいので、∠ABC=∠ACB・・・①
BPは∠ABCの二等分線だから、∠CBP=\(\frac{1}{2}\)∠ABC・・・②
CPは∠ACBの二等分線だから、∠BCP=\(\frac{1}{2}\)∠ACB・・・③
①、②、③より、∠CBP=∠BCP
三角形の2つの角が等しいので、△PBCは二等辺三角形となる。
①から③の角の大きさが等しくなることについて、詳しく説明するね。
角の二等分線は、文字の通り「角を二つに等しく分ける線」ということだから、角BPが角の二等分線の場合、∠ABCをBPが二つに等しく分けた、ということになるんだ。
つまり、∠ABP=∠CBP=\(\frac{1}{2}\)∠ABCということになるよ。
CPも同じように、∠ACP=∠BCP=\(\frac{1}{2}\)∠ACBということになるよ。
そして、∠ABCと∠ACBの大きさが等しいから、それぞれを半分にした∠ABP、∠CBP、∠ACP、∠BCPの4つの角は全て同じ大きさということになるよ。
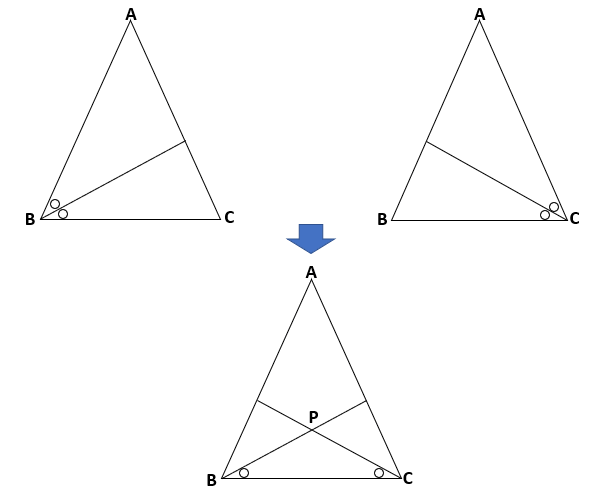
こんな風に二等辺三角形であることを証明していくんだ。
この二等辺三角形、証明問題のテストでは活躍する場面も多いんだ。
たとえば、ある辺と辺が等しいことを証明しなくてはいけないとき、これまでは「合同な図形」を証明して、「合同な図形の対応する辺」だから2辺が等しい、と考えてきたけれど、図形の中の三角形が二等辺三角形であることを証明して、「三角形が二等辺三角形だから長さが等しくなる」、というパターンもあることを覚えておこう!
「二等辺三角形になる条件」まとめ
- 逆とは、あることがらの仮定と結論を入れかえたもの
- 反例とは、あることがらが成り立たない例のこと
- 二等辺三角形になるための条件
➀2辺が等しい
➁2つの角が等しい(底角が等しい)
③頂角の二等分線が底辺を垂直に二等分する
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


