「直角三角形の合同条件」とは？証明問題の解き方をていねいに解説

中学２年生の数学で学習する「直角三角形の合同条件」について、直角三角形とはどんなものか、直角三角形の合同条件にはどんなものがあるのか、なぜそれが合同条件となるのかをわかりやすく解説するよ。

直角三角形の合同条件を使った証明問題の解き方もくわしく解説するよ。

「直角三角形の合同条件」とは？ 証明問題の解き方をていねいに解説のPDF（8枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 直角三角形の斜辺とは
• 直角三角形の合同条件
• 直角三角形の合同条件を使った証明問題
• まとめ

直角三角形の斜辺とは

今回から直角三角形について勉強をしていくよ。
まずは、直角三角形の定義について確認しよう。

漢字で書いたままの定義「直角がある三角形」だね。

次に、直角三角形の辺の名前や角の名前についても確認するよ。

直角三角形の辺の名前や角の名前

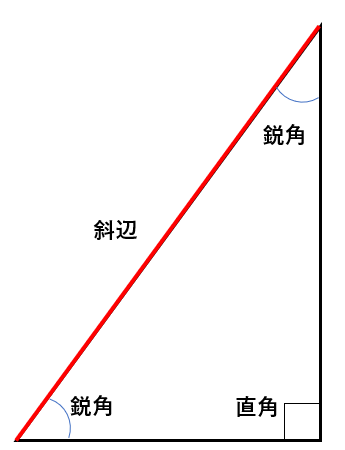
• 鋭角えいかく　０°よりも大きく、９０°よりも小さい角
• 直角ちょっかく　９０°の角
• 斜辺しゃへん　直角に対する（直角に向かい合う）辺
• ※今回は登場していないけれど、９０°よりも大きく、１８０°よりも小さい角を鈍角どんかくというよ。

直角三角形の斜辺については、これからもよく出てくるから忘れずに覚えておこう！

直角三角形の合同条件

直角三角形には、三角形の合同条件とは別に直角三角形にだけ使える限定の合同条件があるんだ。

①『斜辺と１つの鋭角がそれぞれ等しい』ときについて

斜辺と１つの鋭角がそれぞれ等しい２つの直角三角形を例に使って、なぜ合同といえるかを説明するね。

下の図の△ABCと△DEFにおいて、∠ACB＝∠DFE＝９０°、AB＝DE、∠ABC＝∠DEFならば△ABC≡△DEFであることを証明しなさい。

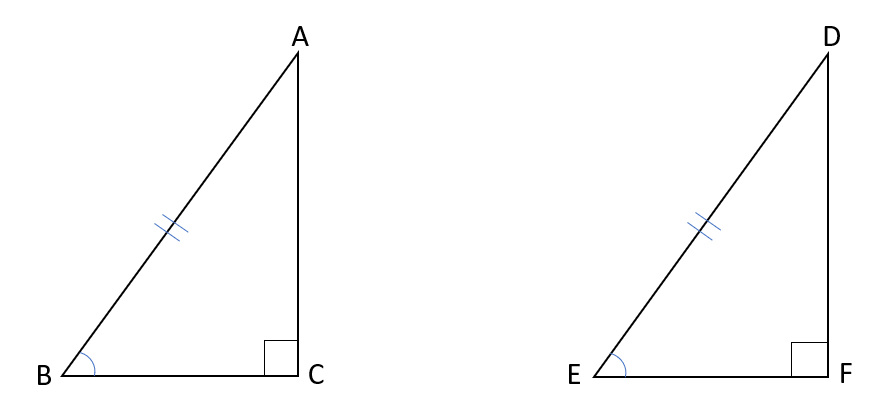
△ABCと△DEFにおいて、
仮定から
∠ACB＝∠DFE＝９０°・・・①
∠ABC＝∠DEF・・・②
AB＝DE・・・③
三角形の内角の和は１８０°だから、
∠BAC＝１８０°－∠ACB－∠ABC
　　 ＝１８０°－９０°－∠ABC
　　 ＝９０°－∠ABC

∠EDF＝１８０°－∠DFE－∠DEF
　　 ＝１８０°－９０°－∠DEF
　　 ＝９０°－∠DEF

②より
∠BAC＝∠EDF・・・④

②、③、④より
１組の辺とその両端の角が等しいので、
△ABC≡△DEF

上の証明のように、三角形の内角の和が１８０°という性質を使うと、３つの角がそれぞれ等しいことがわかるんだ。
そして、斜辺の長さも等しいから、１辺とその両端の角が等しくなって、２つの三角形が合同といえるよ。

直角三角形は、一つの角が９０°と決まっているので、ひとつの鋭角が同じということが決まれば、それは自動的に「もうひとつの鋭角も同じ」になるというのがポイントだね。

②『斜辺と他の１辺がそれぞれ等しい』ときについて

①と同じように、斜辺と１つの鋭角がそれぞれ等しい２つの直角三角形を使って、なぜ合同といえるかを説明するね。

下の図の△ABCと△DEFにおいて、∠ACB＝∠DFE＝９０°、AB＝DE、AC＝DFならば△ABC≡△DEFであることを証明しなさい。

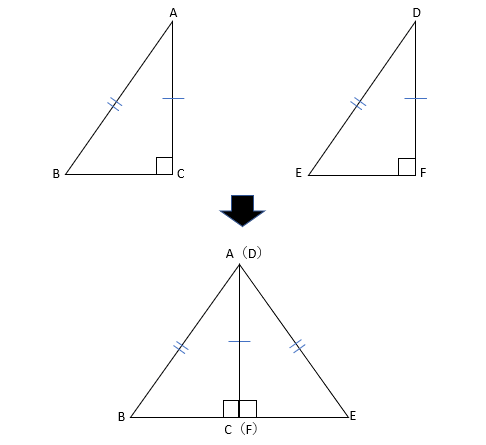
△ABCと△DEFにおいて、仮定よりAC＝DFだから
△DEFを裏返して、上の図のようにACとＤＦを重ねることができる。
このとき、∠ACB＝∠DFE＝９０°だから、∠BCE＝１８０°となり、
３点B、C、Eは１直線上にあることがわかる。

ここで、△ABEにおいて、
仮定から
AB＝DEより
２辺が等しいので、二等辺三角形となる。
二等辺三角形の底角は等しいので、
∠ABC＝∠DEF・・・①

△ABCと△DEFにおいて、
仮定から
∠ACB＝∠DFE＝９０°・・・②
AB＝DE・・・③
AC＝DF・・・④

三角形の内角の和は１８０°だから、
∠BAC＝１８０°－∠ACB－∠ABC
　　 ＝１８０°－９０°－∠ABC
　　 ＝９０°－∠ABC

∠EDF＝１８０°－∠DFE－∠DEF
　　 ＝１８０°－９０°－∠DEF
　　 ＝９０°－∠DEF
①より、
∠BAC＝∠EDF・・・⑤
③、④、⑤より
二組の辺とその間の角がそれぞれ等しいので、
△ABC≡△DEF

二等辺三角形の性質や三角形の内角の和が１８０°という性質を使って、２つの三角形が合同といえるよ。

もし直角三角形の合同条件を使うことができなければ、上のように複雑な流れで合同を証明しなければならないんだ。

直角三角形の合同条件を使った証明問題も三角形の合同条件を使った証明問題と同じように、テストに出やすいから、合同条件は完璧に暗記しよう！

また、直角三角形の合同条件を使う時には、絶対に守らなければならないルールがあるんだ。

それは、

『∠〇〇〇＝∠■■■＝９０°』

というように、必ず直角である角を示す必要があるよ。
これを書かなければ、直角三角形の合同条件は使えないから注意してね。

ではここから、直角三角形の合同条件を使った証明問題にチャレンジしよう。

直角三角形の合同条件を使った証明問題

問題
下の図で、△ABCが二等辺三角形で、MがBCの中点、∠BDM＝∠CEM＝９０°ならば、MD＝MEとなることを証明しなさい。

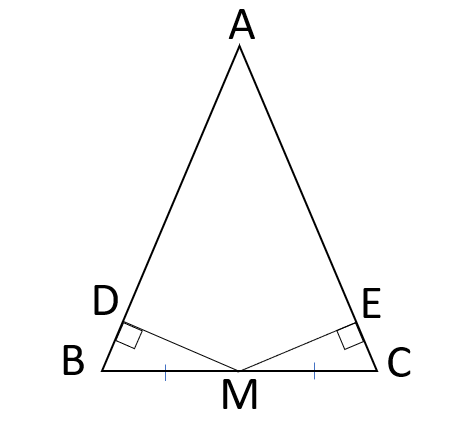
①仮定と結論を問題文から見つけよう。

仮定　△ABCが二等辺三角形、MがBCの中点、∠BDM＝∠CEM＝９０°
結論　MD＝ME

結論を証明するためには、△BDMと△CEMが合同であることを証明する必要があるね。

②仮定からわかることを書こう。

△ABCが二等辺三角形・・・二等辺三角形の性質『二等辺三角形の底角は等しい』から、∠DBM＝∠ECM
※AB＝ACもいえるけれど、△BDMと△CEMの証明には必要ないからカットしているよ。

MがBCの中点・・・BM＝CM

③三角形の合同条件のどれに当てはまるかを考えよう。

②の仮定でわかっていることを図形にかきこむと、直角三角形の合同条件『斜辺と１つの鋭角がそれぞれ等しい』に当てはまることがわかるね。

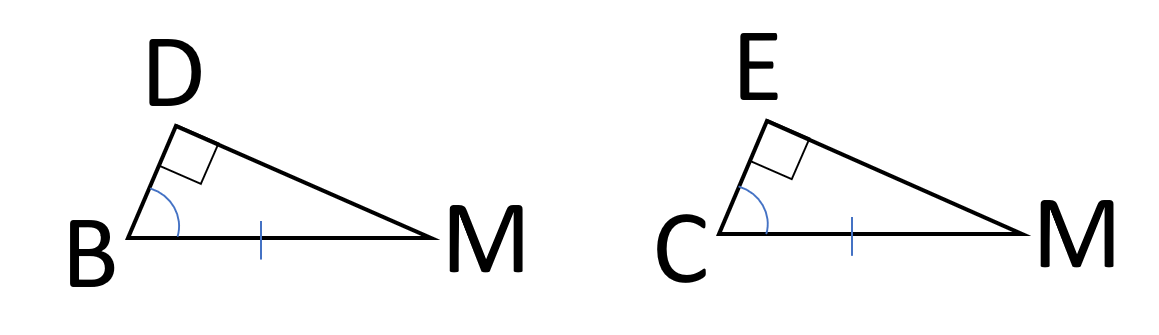
④結論が証明されたことを書こう。

③で△BDM≡△CEMということがわかるので、『合同な図形の対応する辺は等しいから』MD＝MEと書くことができるね。

あとは①から④の内容を整理して解答をかこう。

三角形の合同の証明と同じように、直角三角形の証明もテストにはよく出るから、色々な問題にチャレンジして証明問題に慣れていこう！

「直角三角形の合同」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。