樹形図とは?書き方のコツと注意点をわかりやすく解説(練習問題)
中学校2年生の数学で学習する確率について、「樹形図」とは何か、樹形図の書き方・作り方のコツと注意点をわかりやすく解説するよ。
樹形図を書いて考える練習問題にもチャレンジしてみよう。
樹形図とは
確率の問題を解くときに1番間違いが多いのは、場合の数(何通りかを求める時)の数え間違いなんだ。
そのミスを防ぐために、「樹形図」を書く方法がおすすめだよ。
樹形図は、小学6年生の時にも登場したから覚えている人も多いかな?
樹形図がどんなものだったか忘れてしまった人は、ここでしっかりと復習しておこう。
樹形図とは、起こりうるすべての場合を枝分かれした樹木のようにかいたもののことなんだけれど、言葉だけではイメージしにくいよね。
そこで実際に100円玉1枚と500円玉1枚を投げて表と裏の出方を調べる時、起こりうる場合を樹形図でかくと下の図のようになるよ。(表の時はオ、裏の時はウで表しているよ)
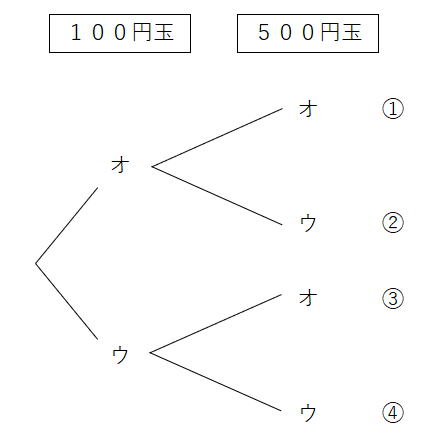
上の図では、
①は100円玉が表、500円玉が表
②は100円玉が表、500円玉が裏
③は100円玉が裏、500円玉が表
④は100円玉が裏、500円玉が裏
を表していて、100円玉1枚と500円玉1枚を投げる時、起こりうる場合は4通りあることがわかるよ。
では次に樹形図の書き方と作り方について確認していこう。
樹形図の書き方
樹形図の書く手順について確認するよ。
樹形図の書く手順
①人や物に名前をつける
②書き漏れが無いように、規則正しく書く
上の樹形図の書く手順を参考にしながら、例題を一緒に解いてみよう。
例題
リレーで4人の生徒が走る順番が何通りあるのか求めなさい。
①人や物に名前をつける
リレーに選ばれた4人の生徒に名前をつけよう。
ここはわかりやすく、A・B・C・Dと名前をつけるね。
②書き漏れが無いように、規則正しく書く
Aが第一走者の場合を樹形図で書いていこう。
次に、第二走者を決めるんだけれども可能性があるのは、B・C・Dだよね。
その場合、上からアルファベット順で書くようにしよう。
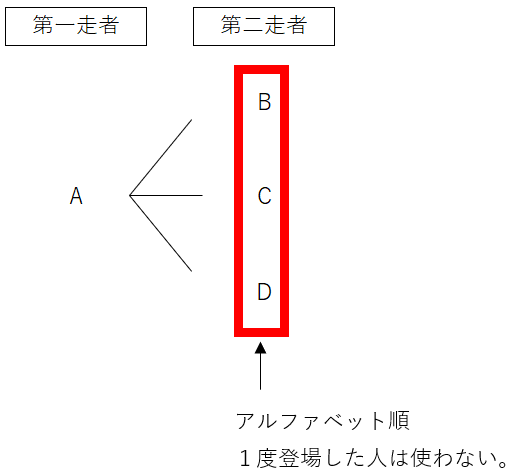
C・D・Bのように、自分の好きな順で書くと書き漏れが出る可能性があるから注意しよう。
また、第一走者にAを書いた場合、第二~第四走者にAを書かないことも気をつけよう。(1人で2回走ることになってしまうよ。)
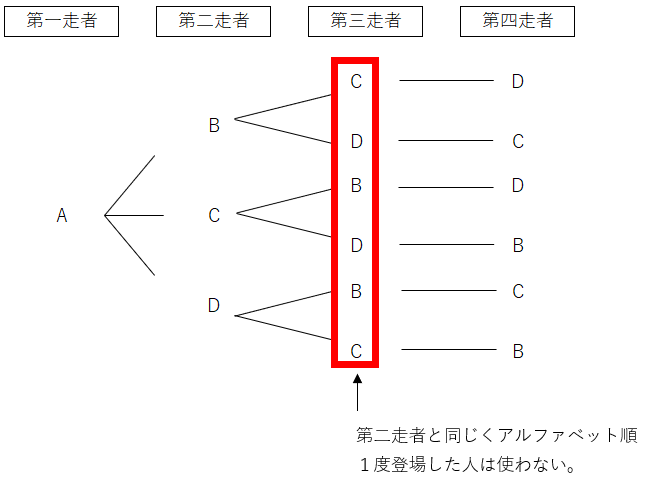
第三走者も第二走者と同じように、まだ走っていない生徒をアルファベット順で書こう。
第三走者を決めると、第四走者は残った1人になるから簡単に見つけることができるね。
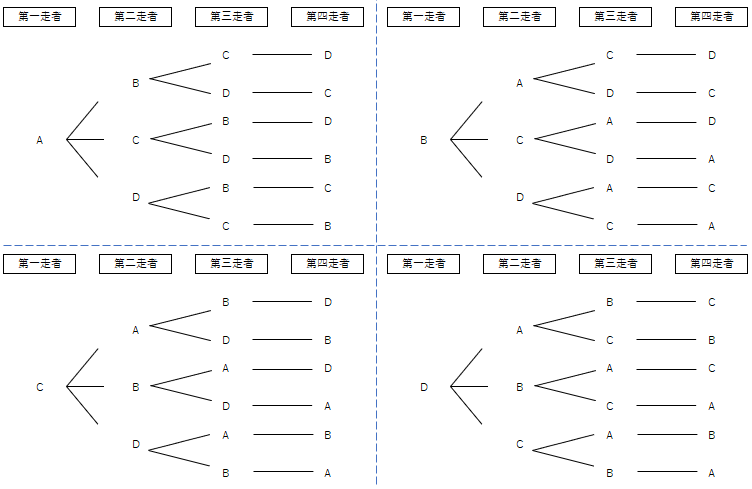
第一走者がB・C・Dの時も同じように書くと、全部で24通りあることがわかるね。
実は第一走者がAの時を求めたら、計算で簡単に全部で何通りあるか求めることができるんだ。
Aが第一走者の時で、6通りあるよね。
B・C・Dの時も同じように、6通りずつあるから
6×4=24
と求めることができるよ。
ただ、全部で何通りあるかを求める問題の時はこれでOKだけれども、「この中でBが第二走者の時は何通り」のような場合には、抜け漏れが発生する時があるから、樹形図を全て書くようにしよう。
樹形図の注意点
樹形図はどんな場合の数でも求めることができるけれども、樹形図を書かずに解いた方が効率的に解ける問題や、樹形図を書く時に注意する問題について説明するよ。
樹形図を使わずに解くパターン:さいころの問題
大小2つのさいころの出た目を使う問題がテストでも出やすいんだけれども、この問題は樹形図ではなく、表を書いて解く方法がおすすめだよ。
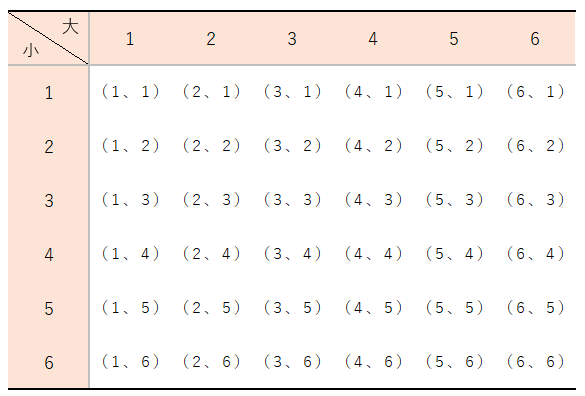
上の表を見てわかるとおり、全部で36通りもあるから樹形図を書くと大変そうだよね。
表にすることで見やすくなるから、「大小2つのさいころの出た目の和が5になるとき」や「大小2つのさいころの出た目の積が奇数になるとき」のようなパターンも簡単に見つけることができるよ。
樹形図を書くときに注意する問題:組み合わせの問題
A・B・C・Dの中から代表者を2人選ぶような問題の時は、注意が必要だよ。
A・B・C・Dの中から「代表と副代表を選ぶ場合」と「代表者2人を選ぶ場合」に分けて違いを見てみよう。
・代表と副代表を選ぶ場合
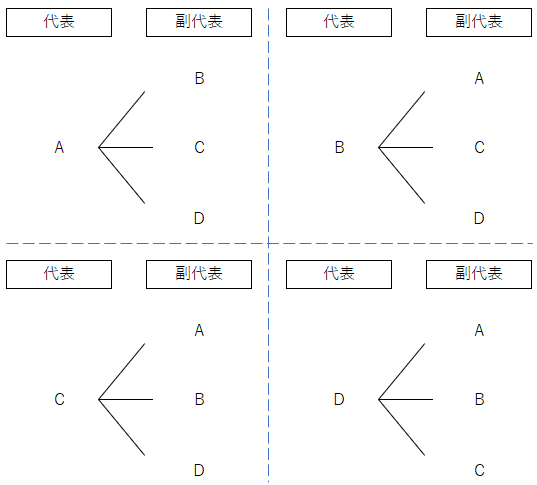
上の樹形図のように、12通りあることがわかるね。
・代表者を2人選ぶ場合
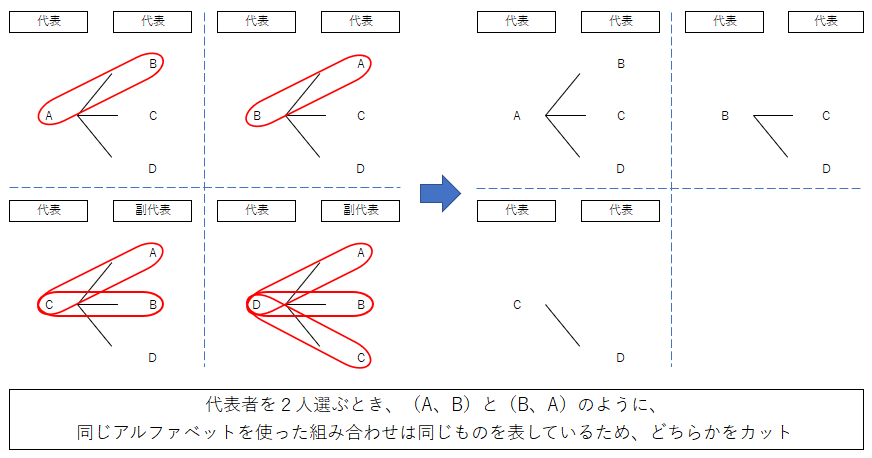
代表者を選ぶ場合、A・Bを選んだ時とB・Aを選んだ時が同じ人の組み合わせになっていることに気がついたかな?
組み合わせを選ぶ時には、「入れ替えたら同じもの」を省略する必要があるから注意しよう。
代表者を2人選ぶときは、6通りになるよ。
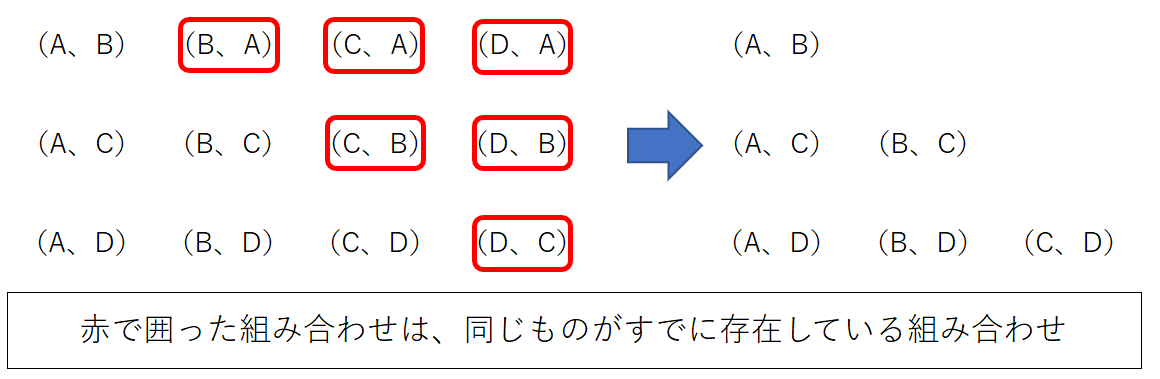
樹形図を書くと省略するものを見落とす心配がある人は、樹形図ではなく上のように(A、B)のように書き出すこともおすすめだよ。
樹形図を使った練習問題
これまで説明した樹形図の知識を使って、練習問題にチャレンジしよう!
問題
1、2、3、4の数を1つずつ記入した4枚のカードがあります。このカードをよくきってから1枚ずつ2回続けてひき、ひいた順にカードを並べて、2けたの整数を作るとき、以下の問に答えなさい。
(1)樹形図をかいて、2けたの整数をすべてあげなさい。
(2)できる整数が奇数になる確率を求めなさい。
(1)
問題の樹形図を書くと、下のようになるよ。
実際に書いたものと見比べてみよう。
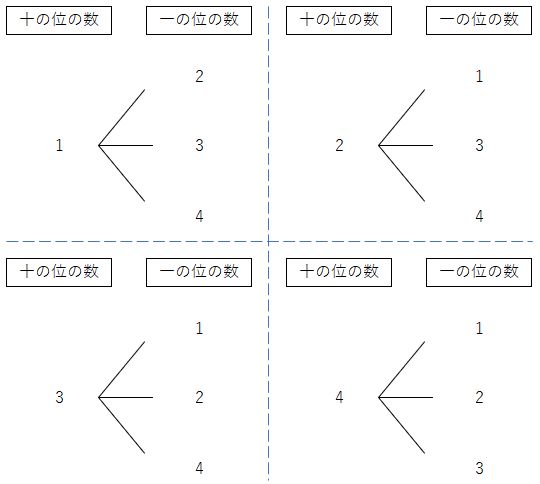
2けたの整数は、小さいものから順に書くと
12、13、14、21、23、24、31、32、34、41、42、43
の12個あるよ。
(2)
(1)の答えから奇数になるのは
13、21、23、31、41、43
の6個あることがわかるね。
奇数になる確率は、\(\frac{できる整数が奇数になる個数}{2けたの整数の個数}\)にあてはめると
\(\frac{6}{12}\)=\(\frac{1}{2}\)
と求めることができるよ。
※確率の求め方がわからなくなってしまっていたら、確率の求め方の解説ページを確認しよう!
樹形図は計算問題の途中式と同じように、省略せずにていねいに書くことでミスを防ぐことができるよ。
樹形図が書き慣れない人は、学校のワークや教科書の問題にどんどんチャレンジしよう。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


